题目
LCR 143. 子结构判断
给定两棵二叉树
tree1和tree2,判断tree2是否以tree1
的某个节点为根的子树具有相同的结构和节点值。注意,空树不会是以tree1的某个节点为根的子树具有相同的结构和节点值。示例:
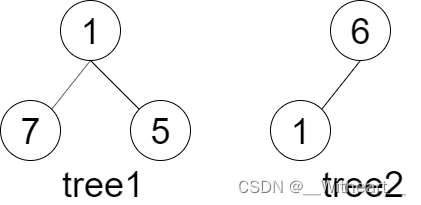
输入:tree1 = [1,7,5], tree2 = [6,1] 输出:false 解释:tree2 与 tree1 的一个子树没有相同的结构和节点值。
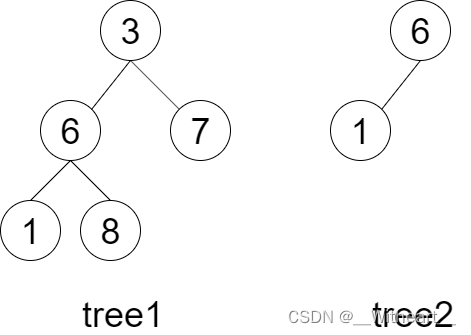
输入:tree1 = [3,6,7,1,8], tree2 = [6,1] 输出:true 解释:tree2 与 tree1 的一个子树拥有相同的结构和节点值。即 6 -> 1。提示:
0 <= 节点个数 <= 10000
一种错误的解法
- 根据观察,我意识到二叉树的先序遍历的序列可能是唯一的,那么如果 tree2 是 tree1 的子结构,其先序遍历序列应该就是 tree1 先序遍历序列的子序列,可以进行子序列的匹配,如果匹配上了就是子结构
- 但实际上,子结构和子树并不是同一个概念,子结构相当于原来树的一部分,而子树是在相当于原来树的一部分的同时,其不能有其他子节点,只能有父结点
- 比如下面这种输入,Tree2 确实是 Tree1 的一部分,但是不是其子树,两棵树的先序遍历结果并不匹配
Tree1:[10,12,6,8,3,11],先序遍历:[10,12,8,3,6,11]
Tree2:[10,12,6,8],先序遍历:[10,12,8,6]
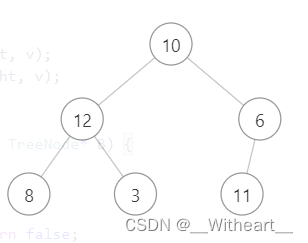
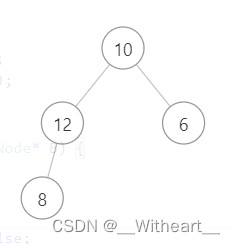
- 所以这种解法是错误的,在此贴上错误代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {vector<int> va, vb;
public://先序遍历void preorder_Traversal(TreeNode* root, vector<int>& v){if(!root) return;v.push_back(root->val);preorder_Traversal(root->left, v);preorder_Traversal(root->right, v);}bool isSubStructure(TreeNode* A, TreeNode* B) {if(!B) return false;//得到两棵树先序遍历的结果preorder_Traversal(A, va);preorder_Traversal(B, vb);if(vb.size()>va.size()) return false;//开始进行序列匹配for(int i=0; i<=va.size()-vb.size(); ++i){auto ita = va.begin()+i, itb=vb.begin();while(*ita==*itb){++ita;++itb;if(itb==vb.end()) return true;//B树匹配完成}}return false;}
};
正确解法:
思想
- 子结构可能与当前节点匹配,或者与当前节点的左子节点匹配,或者与当前节点的右子节点匹配
- 在匹配过程中,使用递归思想,不断匹配。如果匹配成功,则子结构被遍历到空节点;如果有节点不匹配,则匹配失败;如果直到 Tree1 都遍历完成还没匹配上,则也是匹配失败
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool recur(TreeNode* A, TreeNode* B){if(!B) return true;//B树已经越过了叶子节点,匹配成功,返回(最终是否成功由B树的其他部分尝试匹配后确定)if(!A || A->val!=B->val) return false;//已经越过了A的叶子节点,或者A与B节点值不匹配,则匹配失败//本节点匹配相同,AB可能是从此节点开始匹配,则查看其左右子树是否匹配return recur(A->left, B->left) && recur(A->right, B->right);}bool isSubStructure(TreeNode* A, TreeNode* B) {//AB节点要都非空,并且B与A/A->left/A->right可能开始匹配(递归)return (A && B) && (recur(A, B) || isSubStructure(A->left, B) ||isSubStructure(A->right, B));}
};








)




类型趣谈-下)



攻击)

