二叉搜索树（BST）的创建及增，删，查，改（详解）

初识二叉搜索树（BST）：

二叉搜索树查找元素：

二叉搜索树修改元素:

二叉搜索树中的增加元素：

二叉搜索树中的删除元素：

初识二叉搜索树（BST）：

一张图简要概括二叉搜索树：

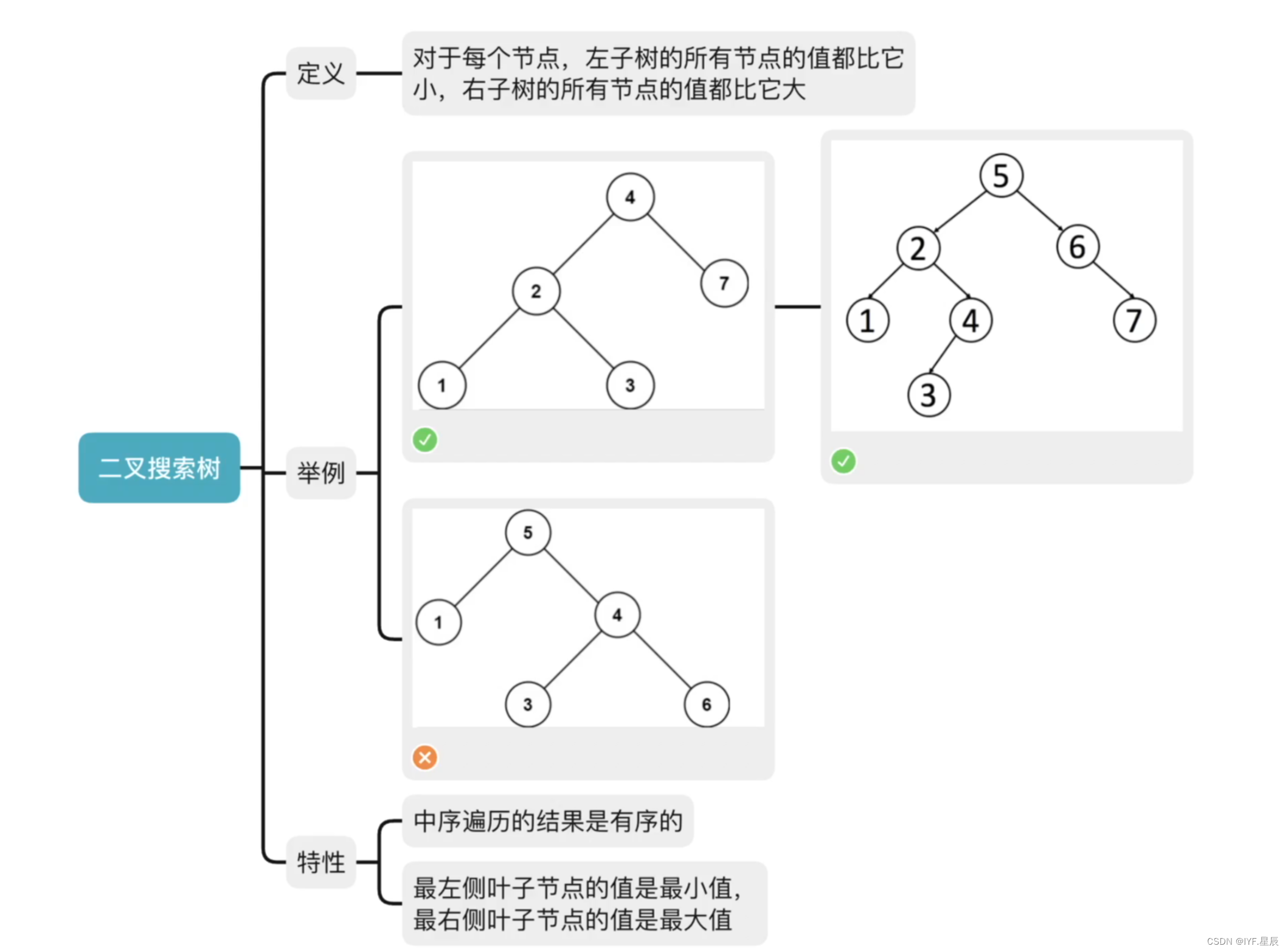
通过定义可知，对于每个节点，左子树的所有节点的值都比它小，右子树的所有节点值都比它大，我们可以很轻易的得出这颗树的最左侧叶子节点的值是最小值，最右侧叶子节点的值是最大值。

那中序遍历为什么一定是有序的呢？原理也很简单，我们先看看二叉树递归的图解：

对于图中的二叉树，中序遍历的结果是：3，2，4，1，7，6，5。按照左子树-》根-》右子树的模式不断递归，结合BST左小右大的特性，那么先得到的值一定是当前树中最小的，同时根是次小的，最后是当前树中最大的。从底部出发，向上不断回溯调用，就得到了顺序的结果。

二叉搜索树查找元素：

题目链接：700. 二叉搜索树中的搜索 - 力扣（LeetCode）

题目描述：

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

如果是在一颗不同的二叉树中搜索（代码如下）：

TreeNode searchBST(TreeNode root, int target);if (root == null) return null;if (root.val == target) return root;// 当前节点没找到就递归地去左右子树寻找TreeNode left = searchBST(root.left, target);TreeNode right = searchBST(root.right, target);return left != null ? left : right;//相当于返回叶子节点
}

其实不需要递归地搜索两边，类似二分查找思想，根据 target 和 root.val 的大小比较，就能排除一边。我们把上面的思路稍稍改动：

TreeNode searchBST(TreeNode root, int target) {if (root == null) {return null;}// 去左子树搜索if (root.val > target) {return searchBST(root.left, target);}// 去右子树搜索if (root.val < target) {return searchBST(root.right, target);}return root;//上面两个都不满足，说明root.val == target直接返回root
}

二叉搜索树修改元素:

无非就是先找到元素对应的位置后再修改该位置对应的值：

TreeNode searchBST(TreeNode root, int target,num) {if (root == null) {return null;}// 去左子树搜索if (root.val > target) {return searchBST(root.left, target);}// 去右子树搜索if (root.val < target) {return searchBST(root.right, target);}root.val = num;//将树中对应的target值改为numreturn root;//上面两个都不满足，说明root.val == target直接返回root
}

二叉搜索树中的增加元素：

这里我们需要更改二叉搜索树的结构：一旦涉及「改」，就类似二叉树的构造问题，函数要返回 TreeNode 类型，并且要对递归调用的返回值进行接收。

TreeNode insertIntoBST(TreeNode root, int val) {// 找到空位置插入新节点if (root == null) return new TreeNode(val);//这里就相当于将节点接入到二叉树对应的叶子中// if (root.val == val)//     BST 中一般不会插入已存在元素if (root.val < val) root.right = insertIntoBST(root.right, val);if (root.val > val) root.left = insertIntoBST(root.left, val);return root;
}

二叉搜索树中的删除元素：

这个问题稍微复杂，跟插入操作类似，先「找」再「改」，先把框架写出来再说：

TreeNode deleteNode(TreeNode root, int key) {if (root.val == key) {// 找到啦，进行删除} else if (root.val > key) {// 去左子树找root.left = deleteNode(root.left, key);} else if (root.val < key) {// 去右子树找root.right = deleteNode(root.right, key);}return root;
}

找到目标节点了，比方说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况，用图片来说明。

情况 1：A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了。

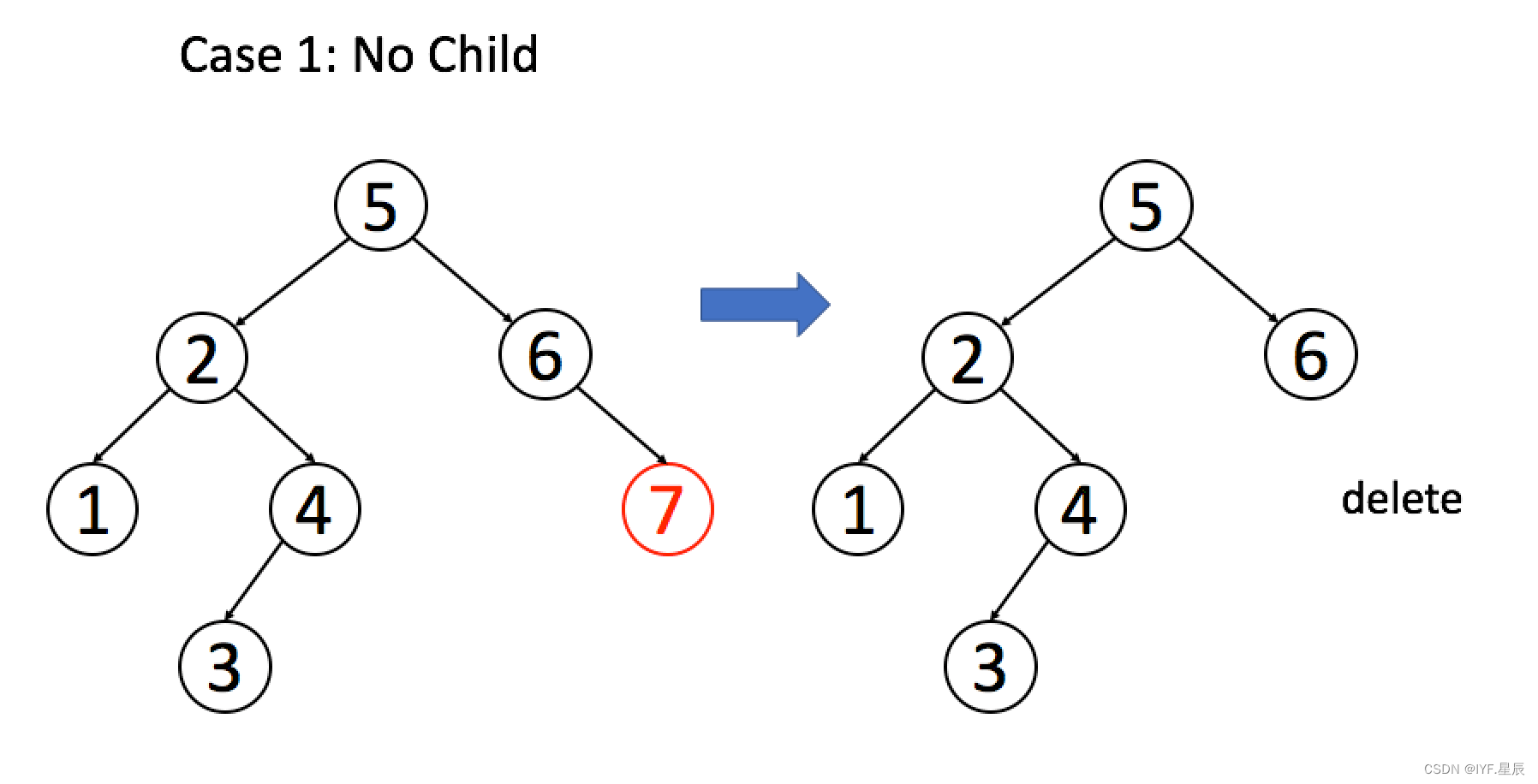
if (root.left == null && root.right == null)return null;

情况 2：A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。

// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;

情况 3：A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。

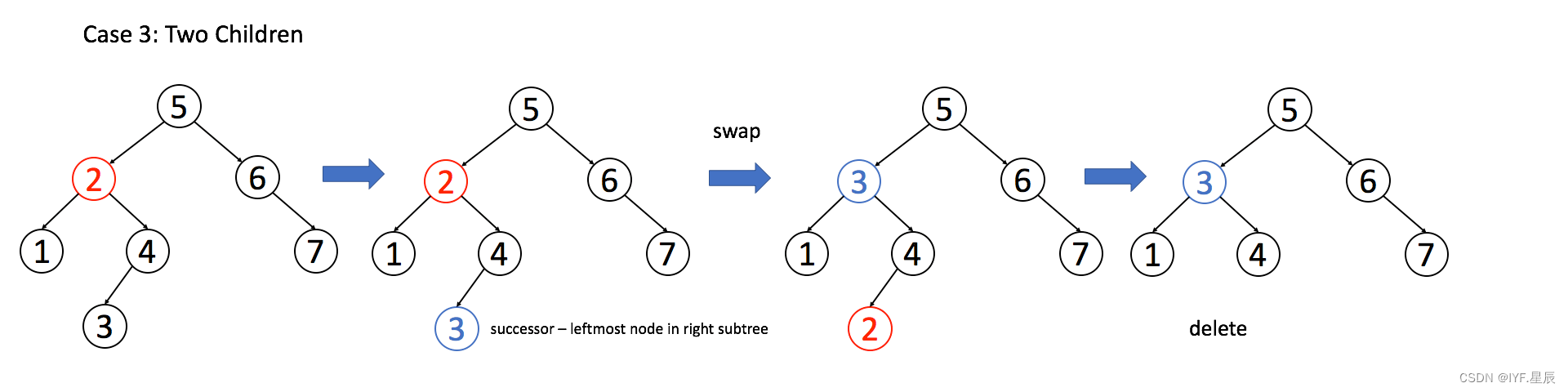
if (root.left != null && root.right != null) {// 找到右子树的最小节点TreeNode minNode = getMin(root.right);// 把 root 改成 minNoderoot.val = minNode.val;// 转而去删除 minNoderoot.right = deleteNode(root.right, minNode.val);
}

三中情况都完成后，整理一下代码：

TreeNode deleteNode(TreeNode root, int key) {if (root == null) return null;if (root.val == key) {// 这两个 if 把情况 1 和 2 都正确处理了if (root.left == null) return root.right;if (root.right == null) return root.left;// 处理情况 3// 获得右子树最小的节点TreeNode minNode = getMin(root.right);// 删除右子树最小的节点root.right = deleteNode(root.right, minNode.val);// 用右子树最小的节点替换 root 节点minNode.left = root.left;minNode.right = root.right;root = minNode;} else if (root.val > key) {root.left = deleteNode(root.left, key);} else if (root.val < key) {root.right = deleteNode(root.right, key);}return root;
}TreeNode getMin(TreeNode node) {// BST 最左边的就是最小的while (node.left != null) node = node.left;return node;
}

参考：《labuladong算法笔记》

结语： 写博客不仅仅是为了分享学习经历，同时这也有利于我巩固自己的知识点，总结该知识点，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注，你们的鼓励是我创作的最大动力！