🎈个人主页：豌豆射手^
🎉欢迎 👍点赞✍评论⭐收藏
🤗收录专栏：机器学习
🤝希望本文对您有所裨益，如有不足之处，欢迎在评论区提出指正，让我们共同学习、交流进步！

引言:

在机器学习的众多步骤中，特征选择是一项至关重要的任务。它不仅影响模型的训练效率和效果，还有助于提高模型的泛化能力和可解释性。

特征选择的方法大致可分为三类：过滤式、包裹式和嵌入式。在这篇博客中，我们将聚焦于包裹式特征选择，特别是基于遗传算法的特征选择方法。

遗传算法是一种模拟自然进化过程的搜索算法，具有全局搜索和快速收敛的特点。

这篇文章将通过详细阐述其原理、步骤、优缺点以及适用场景，并结合Python代码示例，帮助读者更好地理解和应用基于遗传算法的特征选择方法。

一 初步了解

1.1 遗传算法

想要详细了解遗传算法，可以看看这篇博客，这位博主讲得真的太棒啦

遗传算法（Genetic Algorithm, GA）是一种模拟生物进化过程的优化搜索算法。

它基于达尔文的自然选择和遗传学原理，通过模拟选择、交叉、变异等遗传操作，在问题的解空间中寻找最优解。

它将问题的解表示为一组染色体（也称为个体），每个染色体都是问题解空间中的一个候选解。

染色体通常由一串编码组成，这些编码可以是二进制、实数或其他形式，具体取决于问题的性质。

在遗传算法中，初始种群是随机生成的，然后通过迭代过程进行进化。在每一代中，算法根据适应度函数评估每个个体的适应度。

适应度反映了该个体在环境中的生存能力。

适应度函数通常与问题的目标函数相关，用于衡量个体解的优劣。

然后通过选择操作，选择一部分适应度高的个体进入下一代种群。

选择操作通常基于适应度值，旨在保留适应度较高的个体，淘汰适应度较低的个体。常见的选择策略包括轮盘赌选择、锦标赛选择等。

之后便是算法通过交叉操作组合不同个体的基因，生成新的个体。

交叉操作模拟了生物进化中的基因重组过程，通过交换个体的部分基因，产生新的组合，从而增加种群的多样性。

除了交叉操作，再就是通过变异操作随机改变个体的某些基因值，也能生成新的个体。

变异操作模拟了生物在遗传过程中的基因突变，它有助于保持种群的多样性，防止算法过早陷入局部最优解。

就这样通过不断迭代选择、交叉和变异操作，逐步搜索问题的最优解。每一代种群都会根据适应度函数进行更新，直到满足终止条件（如达到最大迭代次数、找到满足性能要求的解等）。

1.2 概念

基于遗传算法的特征选择方法是包裹式特征选择的一种实现，它结合了遗传算法的优化搜索能力与特征选择的需求。

这种方法使用遗传算法的进化机制来搜索最优的特征子集。

在基于遗传算法的特征选择方法中，每个特征子集被编码为一个染色体（或个体），而特征的选择则通过遗传算法中的选择、交叉和变异操作来进行。

在这里，适应度函数用于评估每个特征子集的性能，通常是机器学习模型的性能指标（如分类准确率、回归误差等）。

通过模拟生物进化过程中的选择、交叉和变异机制，基于遗传算法的特征选择方法能够在搜索空间中有效地找到与模型性能高度相关的特征子集。

这种方法在处理高维特征空间、非线性关系以及多峰性能函数时表现出良好的鲁棒性和全局搜索能力。因此，它在机器学习领域中被广泛应用于特征选择和模型优化问题。

1.3 类比

可以用生物进化中的“物种适应环境”的例子来类比基于遗传算法的特征选择方法。

在自然界中，一个物种可能会面临各种各样的环境变化，如气候、食物供应、天敌等。

为了在这些变化中生存和繁衍，物种需要通过进化来适应环境。这种进化过程与基于遗传算法的特征选择方法非常相似。

在这个过程中，物种的基因就是它们的“编码”。每个基因都代表着一种特定的遗传信息，决定了物种的某些特征，如体型、颜色、行为等。

类似地，在特征选择中，我们将特征子集编码为染色体，每个染色体代表着一种特征组合。

另外，一个物种的种群是由许多具有不同基因的个体组成的，这些个体在环境中竞争生存和繁衍的机会。

在特征选择中，我们也初始化一个种群，一个个体就代表一个特征子集，所以种群中包含了许多不同的特征子集组合。

个体在环境中的生存和繁衍能力决定了它本身的适应度。

类似地，在特征选择中，适应度函数用于评估每个特征组合（即每个个体）的优劣，通常与机器学习模型的性能指标相关。

只有适应度较高的个体更有可能生存下来并繁衍后代，这种选择过程确保了优秀的基因能够传递给下一代。

在特征选择中，选择操作也是基于适应度来决定的，我们将会保留适应度较高的特征子集。

此时新个体的产生通常是通过基因交叉（即杂交）来实现的，这种交叉操作有助于产生新的遗传组合，增加物种的多样性，增强物种的适应能力。

在特征选择中，交叉操作也是随机选择两个特征组合，交换它们的部分基因，也就是通过交换部分编码，从而生成新的特征组合。

另外，基因突变也是产生新个体的另一个重要途径，基因突变会随机改变某些基因的表达，从而产生新的遗传特征，这个过程也可能会产生适应度高的新个体。

在特征选择中，变异操作也是以一定的概率随机改变某些特征的选择状态，有助于保持种群的多样性，防止算法过早陷入局部最优解。

因此，物种通过上面的过程，一代又一代的繁衍和适应环境，逐渐进化成更加适应环境的物种。

类似地，在特征选择中，我们也通过多次迭代选择、交叉、变异等操作，生成新的种群，直到找到最优的特征组合。

最终，在生物进化中，适应度最高的物种将主导环境。

在特征选择中，当满足终止条件时，算法将输出最优的特征子集，这个子集是在整个搜索过程中找到的，与机器学习模型的性能指标高度相关。

因此，基于遗传算法的特征选择方法通过模拟生物进化过程，能够在高维特征空间中有效地找到与模型性能高度相关的特征子集，提高模型的预测能力。

二 具体步骤

流程图

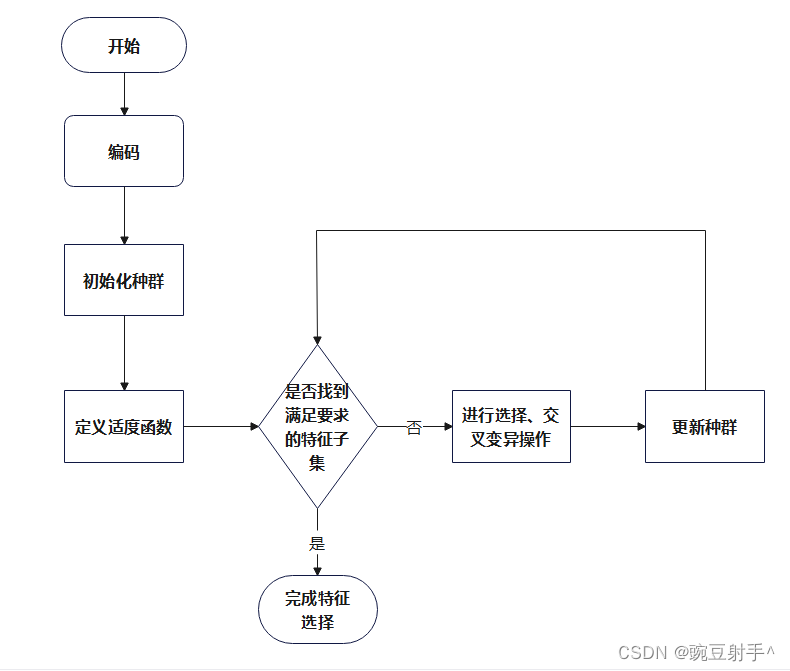
接下来介绍详细的步骤。

2.1 编码

首先，需要将特征子集编码为遗传算法能够处理的染色体。

常用的编码方式包括二进制编码和实数编码。

二进制编码：每个特征对应一个二进制位，1表示选择该特征，0表示不选择。例如，如果有5个特征，一个染色体可以是10101，表示选择第1和第3个特征。

实数编码：使用实数向量表示特征子集的权重或重要性。每个特征对应一个实数，实数的大小表示该特征的重要性程度。

2.2 初始化种群

生成一个初始种群，种群中的每个个体都是一个问题解（即特征子集）的表示。

种群的大小（即个体数量）是一个超参数，需要根据实际问题进行调整。

2.3 定义适应度函数

定义一个适应度函数来评估每个个体（特征子集）的优劣。适应度函数通常与机器学习模型的性能指标相关，如分类准确率、回归误差等。

这个函数将决定哪些个体在进化过程中更有可能被保留下来。

2.4 选择操作

根据适应度函数评估每个个体的适应度，并选择一部分个体进入下一代种群。

选择操作模拟了自然选择的过程，旨在保留适应度较高的个体，淘汰适应度较低的个体。常用的选择策略包括轮盘赌选择、锦标赛选择等。

2.5 交叉操作

随机选择种群中的两个个体，按照一定的交叉概率和交叉方式交换它们的部分基因，生成新的个体。

交叉操作模拟了生物进化中的基因重组过程，有助于产生新的、具有更好性能的特征组合。

2.6 变异操作

以一定的变异概率对种群中的个体进行基因变异，即随机改变某些特征的选择状态。

变异操作模拟了生物在遗传过程中的基因突变，有助于保持种群的多样性，防止算法过早陷入局部最优解。

2.7. 迭代进化

重复执行选择、交叉、变异等操作，生成新的种群。在每一代中，都会根据适应度函数更新个体的适应度值，并根据适应度值进行选择和进化操作。

迭代过程一直持续到满足终止条件，如达到最大迭代次数、找到满足性能要求的特征子集等。

2.8 结果输出

当满足终止条件时，算法停止迭代，并输出最优的特征子集。

这个子集是在整个搜索过程中找到的，与机器学习模型的性能指标高度相关。

基于遗传算法的特征选择方法通过模拟生物进化过程，能够在搜索空间中有效地找到与模型性能高度相关的特征子集。这种方法在处理高维特征空间、非线性关系以及多峰性能函数时表现出良好的鲁棒性和全局搜索能力。

三 优缺点以及适用场景

3.1 优点：

1 全局搜索能力：

遗传算法采用概率化的寻优方法，具有良好的全局搜索能力。

这意味着它能够从整个特征空间中搜索到最优的特征子集，而不仅仅是局部最优解。

2 自适应调整：

遗传算法能够自适应地调整搜索方向，不需要确定的规则或梯度信息。

这使得它在处理非线性、复杂的问题时具有很大的优势。

3 并行性：

遗传算法的搜索过程从群体出发，具有潜在的并行性。

这意味着可以同时评估多个特征子集，提高了搜索效率。

4 可扩展性：

遗传算法容易与其他算法或方法结合，具有良好的可扩展性。

例如，可以与其他特征选择方法、机器学习模型等相结合，进一步提高性能。

3.2 缺点：

1 计算复杂度高：

遗传算法需要多次迭代和评估，计算开销较大。

特别是在处理高维特征空间时，计算成本可能会显著增加。

2 参数选择敏感：

遗传算法涉及多个参数，如交叉率、变异率等。

这些参数的选择对算法性能有很大影响，而选择合适的参数通常需要经验或实验确定。

3 可能陷入局部最优：

虽然遗传算法具有全局搜索能力，但在某些情况下，它也可能陷入局部最优解。

这通常与参数选择、初始种群设置等因素有关。

3.3 适用场景：

1 高维特征空间：

当特征数量很多时，基于遗传算法的特征选择方法能够有效地从中搜索到最优的特征子集，降低特征维度，提高模型性能。

2 非线性关系：

对于具有非线性关系的数据集，基于遗传算法的特征选择方法能够自适应地调整搜索方向，找到与模型性能高度相关的特征组合。

3 复杂优化问题：

当特征选择问题非常复杂，难以用其他方法解决时，基于遗传算法的特征选择方法可能是一个有效的选择。

总之，基于遗传算法的特征选择方法在机器学习中具有独特的优势和适用场景。它能够在高维特征空间中有效地搜索到最优的特征子集，提高模型性能。

然而，也需要注意其计算开销大、参数选择敏感等缺点，并根据实际问题选择合适的参数和方法。

四 代码示例及分析

在Python中实现基于遗传算法的包裹式特征选择方法，首先需要安装和导入必要的库，如numpy用于数值计算，sklearn用于机器学习和数据处理，以及deap库，它是一个用于进化算法的强大框架。

然后，定义适应度函数，该函数将评估每个特征子集在机器学习模型上的性能。

接着，使用deap库创建遗传算法所需的工具，如初始化种群、定义交叉和变异操作、选择操作等。

以下是具体的步骤：

4.1 导入必要的库

import random  
import numpy as np    
from sklearn.datasets import load_iris    
from sklearn.model_selection import cross_val_score    
from sklearn.tree import DecisionTreeClassifier    
from deap import base, creator, tools, algorithms

分析：

numpy 是一个用于数值计算的库，这里用于后续计算模型的交叉验证分数。

load_iris 用于加载著名的鸢尾花数据集。

cross_val_score 用于评估模型的交叉验证性能。

DecisionTreeClassifier 是scikit-learn中的一个决策树分类器。

deap 是一个用于进化算法的Python库，这里用于遗传算法的特征选择。

4.2 加载数据集

data = load_iris()    
X, y = data.data, data.target

分析：

使用load_iris函数加载鸢尾花数据集。
X 是特征矩阵，y 是目标向量。

4.3 定义适应度函数

def evaluate_fitness(individual):    selected_features = [i for i, bit in enumerate(individual) if bit]    X_selected = X[:, selected_features]    model = DecisionTreeClassifier()    score = np.mean(cross_val_score(model, X_selected, y, cv=5))    return score,

分析：

这个函数用于评估一个特征子集（由individual表示，其中1表示选择该特征，0表示不选择）的性能。

首先使用列表推导式将二进制编码转换为特征索引。

再使用这些特征索引从原始特征矩阵X中选择特征，接着使用选定的特征训练决策树分类器，并使用交叉验证评估其性能。

最后返回交叉验证分数的平均值作为适应度值。

4.4 创建遗传算法所需的数据结构和工具

creator.create("FitnessMax", base.Fitness, weights=(1.0,))    
creator.create("Individual", list, fitness=creator.FitnessMax)    
toolbox = base.Toolbox()    
toolbox.register("attr_bool", random.randint, 0, 1)    
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n=X.shape[1])    
toolbox.register("population", tools.initRepeat, list, toolbox.individual)    
toolbox.register("evaluate", evaluate_fitness)    
toolbox.register("mate", tools.cxTwoPoint)    
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)    
toolbox.register("select", tools.selTournament, tournsize=3)

分析：

使用creator模块创建了两个新的类：FitnessMax（用于存储适应度值）和Individual（表示一个个体，即一个特征子集）。

并创建了一个toolbox对象，用于注册后续遗传算法所需的函数和参数。

4.5 初始化种群和遗传算法参数

pop = toolbox.population(n=50)    
CXPB, MUTPB, NGEN = 0.5, 0.2, 40

分析：

使用toolbox.population函数初始化了一个包含50个个体的种群。
设置了交叉概率（CXPB）、变异概率（MUTPB）和迭代次数（NGEN）。

4.6 运行遗传算法

algorithms.eaSimple(pop, toolbox,CXPB, MUTPB, NGEN, verbose=True)

分析：

使用deap库中的eaSimple函数运行遗传算法。
传入了种群、工具箱、交叉概率、变异概率、迭代次数和verbose=True（表示在运行时输出信息）。

4.7 提取最优解

best_ind = tools.selBest(pop, 1)[0]    
best_features = [i for i, bit in enumerate(best_ind) if bit]
for i, bit in enumerate(best_ind) if bit]
print("最优特征子集:", best_features)

分析：

使用tools.selBest函数从种群中选择适应度最高的个体。

从选出的最佳个体中提取出被选中的特征索引，即值为1的位置。

打印出最优的特征子集。

将上述代码段整合后，整体代码的功能是利用遗传算法来优化鸢尾花数据集的特征选择，通过不断迭代，找到使得决策树分类器性能最好的特征子集。

运行结果：

最优特征子集: [0, 1, 2, 3]

这表示在第0、1、2和3列的特征被选中作为最优特征子集。

这里的数字索引对应于鸢尾花数据集中的特征，这些特征分别是花萼长度、花萼宽度、花瓣长度和花瓣宽度。

要获得确切的输出，您需要在具有所需库的Python环境中运行代码。由于遗传算法的性质，您可能需要多次运行代码以获得一致的结果，因为算法可能陷入局部最优解。

完整代码：

import numpy as np 
import random 
from sklearn.datasets import load_iris  
from sklearn.model_selection import cross_val_score  
from sklearn.tree import DecisionTreeClassifier  
from deap import base, creator, tools, algorithms  # 加载数据集  
data = load_iris()  
X, y = data.data, data.target  # 定义适应度函数  
def evaluate_fitness(individual):  # 将二进制编码转换为特征索引  selected_features = [i for i, bit in enumerate(individual) if bit]  X_selected = X[:, selected_features]  # 使用选定的特征训练模型并评估性能  model = DecisionTreeClassifier()  score = np.mean(cross_val_score(model, X_selected, y, cv=5))  return score,  # 返回性能指标（如准确率）  # 创建遗传算法所需的数据结构和工具  
creator.create("FitnessMax", base.Fitness, weights=(1.0,))  
creator.create("Individual", list, fitness=creator.FitnessMax)  toolbox = base.Toolbox()  
toolbox.register("attr_bool", random.randint, 0, 1)  
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n=X.shape[1])  
toolbox.register("population", tools.initRepeat, list, toolbox.individual)  
toolbox.register("evaluate", evaluate_fitness)  
toolbox.register("mate", tools.cxTwoPoint)  
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)  
toolbox.register("select", tools.selTournament, tournsize=3)  # 初始化种群和遗传算法参数  
pop = toolbox.population(n=50)  
CXPB, MUTPB, NGEN = 0.5, 0.2, 40  # 交叉概率、变异概率和迭代次数  # 运行遗传算法  
algorithms.eaSimple(pop, toolbox, CXPB, MUTPB, NGEN, verbose=True)  # 提取最优解  
best_ind = tools.selBest(pop, 1)[0]  
best_features = [i for i, bit in enumerate(best_ind) if bit]  
print("最优特征子集:", best_features)

总结

通过本文的探讨，我们深入了解了基于遗传算法的特征选择方法。

该方法通过模拟自然进化过程，实现了对特征子集的智能优化，为机器学习模型的构建提供了有效的特征选择手段。

其优点包括全局搜索能力强、易于实现并行化、能够处理大规模数据集等；然而，也存在计算复杂度较高、参数调整困难等缺点。在实际应用中，我们需要根据具体的数据集和问题特点，权衡其优缺点，选择最合适的特征选择方法。

通过代码示例的分析，我们进一步理解了基于遗传算法的特征选择方法在实际操作中的应用。

在实际使用中，我们需要结合具体的机器学习任务，调整编码方式、适应度函数、选择操作、交叉操作和变异操作等步骤，以获得最佳的特征子集。

同时，我们还需要注意算法的性能优化和结果的可解释性，以便更好地服务于后续的机器学习模型构建和数据分析工作。

总之，基于遗传算法的特征选择方法是一种强大而灵活的特征选择手段，它能够在复杂的特征空间中寻找到最优的特征子集，提高机器学习模型的性能和可解释性。

通过本文的介绍和代码示例的展示，相信读者已经对该方法有了更深入的理解和掌握，期待在未来的机器学习任务中能够灵活运用这一方法，取得更好的效果。

这篇文章到这里就结束了

谢谢大家的阅读！

如果觉得这篇博客对你有用的话，别忘记三连哦。

我是豌豆射手^，让我们我们下次再见