
欢迎来到Cefler的博客😁
🕌博客主页:折纸花满衣
🏠个人专栏:题目解析
🌎推荐文章:【LeetCode】winter vacation training

目录
- 👉🏻完全背包
👉🏻完全背包
原题链接:完全背包
mycode1(超出时间限制):
#include <iostream>
#include<vector>
using namespace std;int main() {int n, V;cin >> n >> V;vector<int> w(n + 1), v(n + 1);// vector<vector<int>> goods(n,vector<int>(2));for (int k = 1; k <= n; k++) cin >> v[k] >> w[k];//创建dp表vector<vector<int>> dp1(n + 1, vector<int>(V + 1)), dp2(n + 1, vector<int>(V + 1));//dp表初始化for (int k = 1; k < V + 1; k++){dp2[0][k] = -1;}//开始填表for (int i = 1; i < n + 1; i++){for (int j = 1; j < V + 1; j++){// dp1[i][j]特征方程dp1[i][j] = dp1[i - 1][j];int num = 1;if (j - v[i] >= 0){dp1[i][j] = max(dp1[i][j], w[i] * num + dp1[i - 1][j - v[i] * num]);//一定要在这个位置先放一个,可能第一个就是最大(调试出来的血泪)for (; j - v[i] * num >= 0; num++){dp1[i][j] = max(dp1[i][j], w[i] * num + dp1[i - 1][j - v[i] * num]);}//--num;//因为此时j - v[i] * num已经<0所以此时要--num恢复j - v[i] * num >= 0的num状态//dp1[i][j] = max(dp1[i][j], w[i] * num + dp1[i - 1][j - v[i] * num]);}//dp2[i][j]特征方程num = 1;//num重新初始化为1dp2[i][j] = dp2[i - 1][j];if (j - v[i] >= 0 && dp2[i ][j - v[i]] != -1){dp2[i][j] = max(dp2[i][j], w[i] * num + dp2[i][j - v[i] * num]);//一定要在这个位置先放一个,可能第一个就是最大(调试出来的血泪)for (; j - v[i] * num >= 0 && dp2[i][j - v[i] * num] != -1; num++){dp2[i][j] = max(dp2[i][j], w[i] * num + dp2[i][j - v[i] * num]);}//--num;//因为此时j - v[i] * num已经<0所以此时要--num恢复j - v[i] * num >= 0的num状态//dp2[i][j] = max(dp2[i][j], w[i] * num + dp2[i][j - v[i] * num]);}}}cout << dp1[n][V] << endl;cout << (dp2[n][V] == -1 ? 0 : dp2[n][V]) << endl;
}
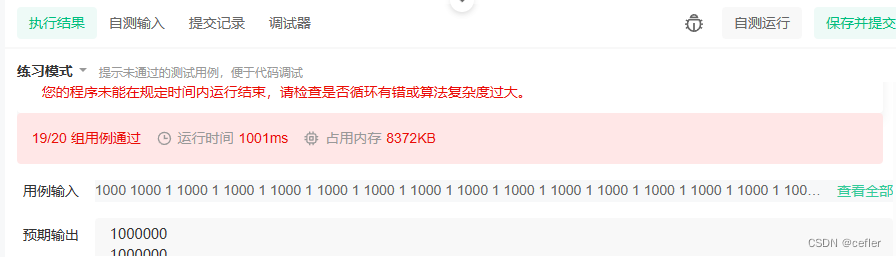
我好不容易心动一次,你却让我输得这么彻底~呵呵
优化代码:

这里主要优化了状态转移方程
mycode2:
#include <iostream>
#include<vector>
using namespace std;
int main() {int n, V;cin >> n >> V;vector<int> w(n + 1), v(n + 1);// vector<vector<int>> goods(n,vector<int>(2));for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];//创建dp表vector<vector<int>> dp1(n + 1, vector<int>(V + 1)), dp2(n + 1, vector<int>(V + 1));//dp表初始化for (int i = 1; i < V + 1; i++){dp2[0][i] = -1;}//开始填表for (int i = 1; i < n + 1; i++){for (int j = 0; j < V + 1; j++){//dp1[i][j]特征方程dp1[i][j] = dp1[i - 1][j];if (j - v[i] >= 0)dp1[i][j] = max(dp1[i][j], w[i] + dp1[i ][j - v[i]]);//dp2[i][j]特征方程dp2[i][j] = dp2[i - 1][j];if (j - v[i] >= 0 && dp2[i][j - v[i]] != -1)dp2[i][j] = max(dp2[i][j], w[i] + dp2[i][j - v[i]]);}}cout << dp1[n][V] << endl;cout << (dp2[n][V] == -1 ? 0 : dp2[n][V]) << endl;
}
—— 最大汇聚运算)
修改用户头像与昵称)


)










![【洛谷 P8707】[蓝桥杯 2020 省 AB1] 走方格 题解(动态规划)](http://pic.xiahunao.cn/【洛谷 P8707】[蓝桥杯 2020 省 AB1] 走方格 题解(动态规划))
:如何使用eBPF绘制网络拓扑图)

)
