目录

例1

例2

例3

例4

例5

例6

---

例1

62. 不同路径

 

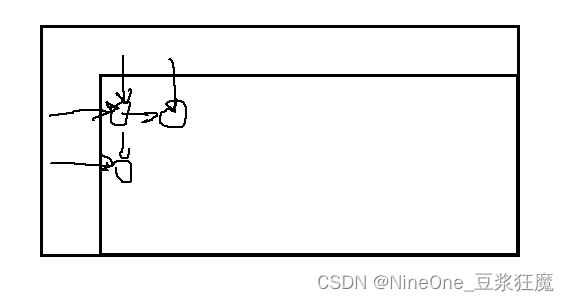
1.初始化

2.当前位置的条数，就是上面位置的条数 ，加上其左边位置的条数，dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

参考代码

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1;for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];return dp[m][n];}
};

例2

63. 不同路径 II

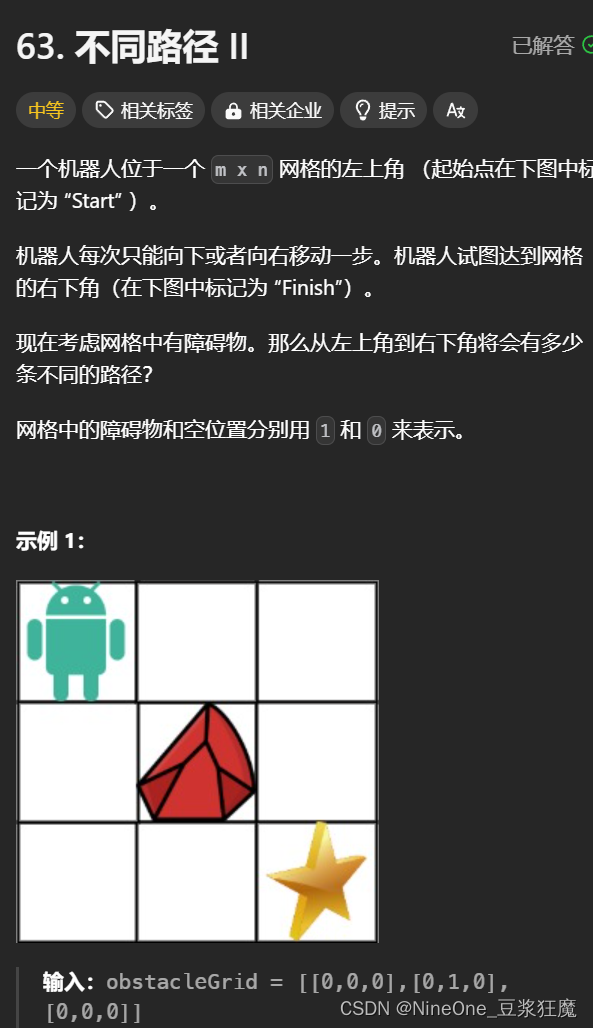
1.初始化dp

2.将obstacleGrid中为0 的值映射到dp表中为0即可

参考代码

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size(), n = obstacleGrid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1;for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)if(obstacleGrid[i - 1][j - 1] == 0)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];return dp[m][n]; }
};

例3

LCR 166. 珠宝的最高价值

初始化默认为0，且题目中说了，价值都是大于0

因为是求右下角的值，那么dp就是从左上往右下

参考代码

class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m = frame.size(), n = frame[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];return dp[m][n];}
};

例4

931. 下降路径最小和

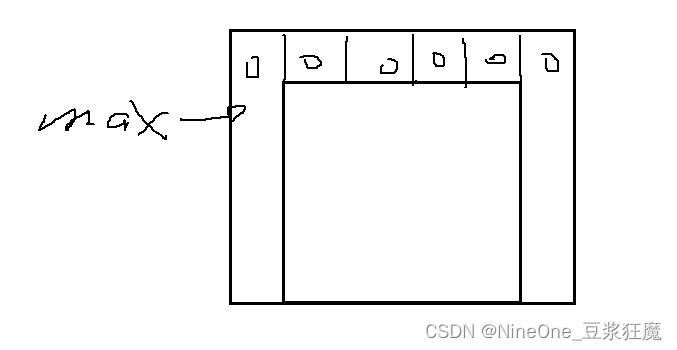
注意：如果没有这一行for(int i = 0; i < n + 2; i++) dp[0][i] = 0;会溢出，如果改成longlong的vector，那么这时候min会出现没有匹配的模版，因为类型不同，并不是min写错了，官方文档

参考代码

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));for(int i = 0; i < n + 2; i++) dp[0][i] = 0;for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];int ret = INT_MAX;for(int i = 1; i <= n; i++)ret = min(ret, dp[n][i]);//没有int和long long 的比较return ret;}
};

例5

64. 最小路径和

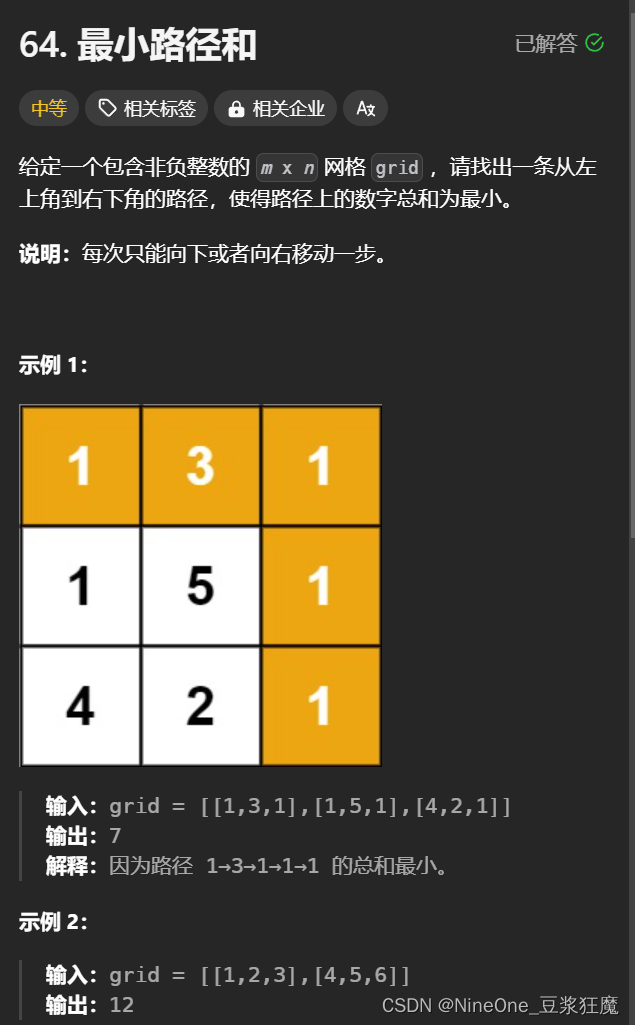
 最小：：：初始化为INT_MAX；

dp[0][1] = 0方便dp[1][1]

映射

参考代码

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[0][1] = 0;for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];return dp[m][n];}
};

例6

174. 地下城游戏

 求的是dp[0][0]，那么就是从左下往右上填写dp表

这里不用映射

dp表里的值代表的是+-之后的血量，dp[m][n - 1] = dp[m - 1][n] = 1;这一步代表走到这俩位置还能保持一格血，这俩位置不会+-血，也就是 +- 完dp[m - 1][n - 1]后还剩下1滴血

 dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];等价于：当前需要的血量 = 下一步较小的血量 - 需要+-的血量，如果所需是0，则改成1

参考代码

class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m = dungeon.size(), n = dungeon[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[m][n - 1] = dp[m - 1][n] = 1;for(int i = m - 1; i >= 0; i--)for(int j = n - 1; j >= 0; j--){dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];dp[i][j] = max(1, dp[i][j]);}return dp[0][0];}
};