适用平台：Matlab+Yalmip+Cplex

程序在建立电厂与碳捕集装置协同调度模型的基础上，引入信息间隙决策理论(information gap decision theory, IGDT)以同时满足系统的鲁棒性和经济性要求，通过风险追求和风险规避２种决策角度得到不同的调度方案。程序算例丰富、注释清晰、干货满满，可扩展性和创新性很高！码超所值！下面对文章和程序做简要介绍！

程序创新点：

1）将该系统在不确定性下的调度分为机会模型( opportuneness model, OM )和鲁棒模型(robustness model, RM)２种，前者偏投机，后者偏向保守。

2）在进行调度优化时，研究者需考虑负荷的不确定性并对调度方案进行决策指导。这里采用IGDT方法优化负荷的不确定性。

主要工作：

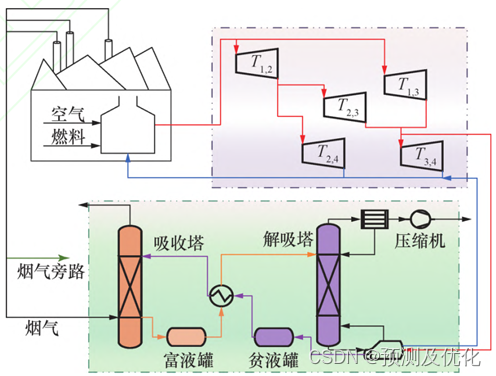
作为目前最有潜力的大规模商业化减碳手段之一，基于化学溶剂吸收的燃烧后碳捕集技术有望实现化石能源的清洁使用。在燃煤火电厂动态运行的基础上耦合碳捕集系统对于推动“碳中和”进程具有重要意义。但是，大多数研究没有考虑诸如用电价格波动和用电量的变化等因素对耦合碳捕集系统的电厂的影响。为此，该文在建立电厂与碳捕集装置协同调度模型的 基础上，引入信息间隙决策理论(information gap decision theory，IGDT)以同时满足系统的鲁棒性和经济性要求，通过风险追求和风险规避２种决策角度得到不同的调度方案，为系统的动态运行提供指导性意见。该文首先构建了确定性电厂与碳捕集装置耦合调度模型；其次，针对实时市场中负荷需求的不确定性，通过引入信息间隙决策理论，得到不同风险态度下的不确定性电厂与碳捕集装置耦合调度模型，优化确定系统调度的决策方案。

主要框架：

1. 信息间隙理论-IGDT

IGDT是处理非概率不确定性的决策方法。常用的随机规划方法难以优化此类无法用概率或场景表示的不确定性。同时，因模型设置了预期成本或利润指标，在优化中可同时保证系统鲁棒性和基本经济性，优于传统的鲁棒优化方法。不同于鲁棒优化精确的上下限范围集合，

IGDT的不确定因素输入为一个不精确的集合，并通过一些非概率模型的不确定集描述不确定性如包络模型、分数不确定性模型和椭球模型等。

2. 基于风险追求的机会IGDT调度模型

机会IGDT模型认为实时市场电力负荷的不确定性可使调度朝经济有利的方向发展。在风险追求调度决策下，不确定性调度模型的目标是最小化不确定度，即要保证在负荷波动幅度内的系统日利润要大于期望利润，且尽可能降低追求不确定性带来的风险，从而获得更大的收益。因此，建立了基于风险追求的机会IGDT碳捕集电厂调度模型，表示如下：

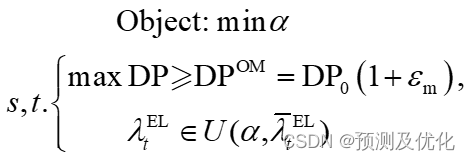
上式为双层规划模型，下层的目标函数通过风险追求调度决策优化使利润最大化，在该模型中实时负荷需求限制在不确定集内；上层的目标函数为最小化负荷的不确定度。其中：εm为机会偏差因子，DPOM为机会收益阈值，DP0为确定性碳捕集电厂调度模型(或称为风险中性模型，neutral model，NM)的最优值，该确定性模型是基于不确定性的预测值构建的。决策方案的机会性使得下层模型的目标利润大于DP0，因此εm的取值为[0,1），且与决策对风险追求的程度呈正比。对于碳捕集电厂而言，考虑负荷的调度方案与以电价为导向的调度方案相比，其日利润有所下降。此时，风险追求调度决策下负荷需求约束越小，越能获得收益。对于上式来说，当实时负荷需求取值为不确定集的下限λELt＝λELt(1－α)时，下层模型的日利润能达到最大值, 因而可将双层规划模型转化为下述单层优化模型：

3. 基于风险规避的鲁棒IGDT调度模型

鲁棒IGDT模型认为负荷的不确定性会影响系统调度结果。在风险规避调度决策下，碳捕集电厂希望在保证基本的经济性的前提下实现鲁棒性最优，即求得不确定参数波动的极限值使得碳捕集电厂的日利润能够满足期望值，因此建立的基于风险规避的鲁棒IGDT碳捕集电厂调度模型为：

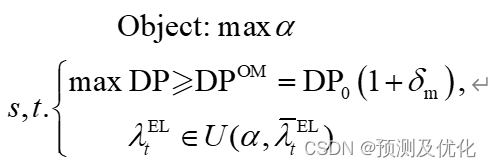
其中：δm为鲁棒偏差因子，DPRM为鲁棒收益阈值.同理，δm的取值范围为[0,1)，且与决策对风险的规避程度呈正比。同时，对于上式来说，当实时负荷需求为λELt＝λELt(1+α)时，即为不确定集的上界时。下层模型能取得最小值。同理。可将上式转化为：

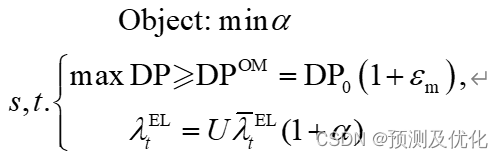
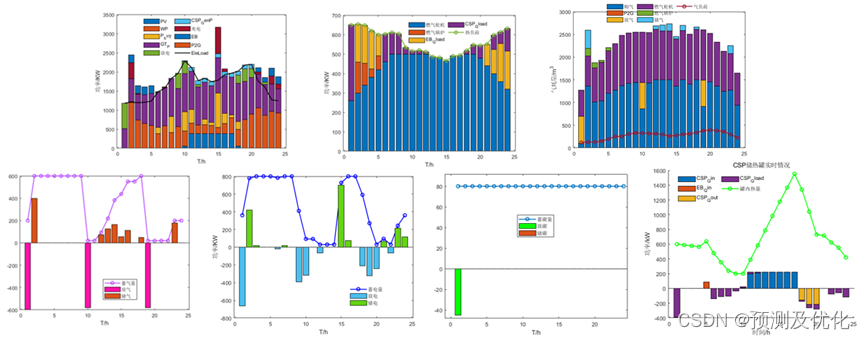
程序结果：

1. 基于风险追求的机会IGDT 调度模型

2. 基于风险规避的鲁棒IGDT 调度模型

---

部分程序：

%%  定义信息间隙决策理论增加变量
HeatLoad=sdpvar(1,24);%实际热负荷​EleLoad=sdpvar(1,24);%实际电负荷
P_v_pre=sdpvar(1,24);%实际光伏​P_w_pre=sdpvar(1,24);%实际风电
gasLoad=sdpvar(1,24);%实际气负荷​C_CO2=sdpvar(1,1);%碳交易成本
% 购电
state=binvar(1,24,'full'); % 判断是否售电，1购电，0不购电
​P_buy = sdpvar(1,24,'full'); % 购电功率
% 燃气轮机​
GT_Q = sdpvar(1,24,'full'); % 燃气轮机的产热量
C_GT= sdpvar(1,24,'full'); % 燃气轮机碳排放
% 燃气锅炉
GB_G = sdpvar(1,24,'full'); % 燃气锅炉气耗量
GB_Q = sdpvar(1,24,'full'); % 燃气轮机的产热量
% 电锅炉
EB= sdpvar(1,24,'full');​EB_Q= sdpvar(1,24,'full');
EB_Qin=sdpvar(1,24,'full'); % 电锅炉供给CSP的热量
EB_Qload= sdpvar(1,24,'full');
% 储气装置
GS_S = sdpvar(1,24,'full'); %储气罐的储热量​GS_Qout = sdpvar(1,24,'full'); %储气罐的放热功率
% 电储能储装置
PS_S = sdpvar(1,24,'full'); ​PS_Qout = sdpvar(1,24,'full');
% 购气
Gas = sdpvar(1,24,'full'); % 购买的天然气量​P2G= sdpvar(1,24,'full'); % 电转气
G_P2G= sdpvar(1,24,'full'); % 电转气
% 光热​
CSP_S=sdpvar(1,24,'full'); % CSP中的储热罐的储热量​CSP_Qin=sdpvar(1,24,'full'); % CSP中的储热罐充热功率
CSP_Qout=sdpvar(1,24,'full'); % CSP的储热罐放热功率CSP_SU=sdpvar(1,24,'full'); % CSP用于启动汽轮机的热量​
% 碳捕集
CCS=sdpvar(1,24,'full'); %  碳捕集量​P_CCS=sdpvar(1,24,'full'); % 碳捕集能耗
CCS_P2G=sdpvar(1,24,'full'); % 供给P2G​CCS_S_in=sdpvar(1,24,'full'); % 储碳
CCS_S_out=sdpvar(1,24,'full'); % 放碳​
%% 碳捕集​​CCS(t)<=0.98*C_GT(t),P_CCS(t)==0.26*CCS(t)+3,CCS(t)==CCS_P2G(t)+CCS_S_in(t),​G_P2G(t)==2*(CCS_P2G(t)+CCS_S_out(t)),20<=CCS_S(t)<=150,CCS_S_lamda(t)*150*0.3>=CCS_S_out(t)>=0,​
%% 光热电站​%热量传递约束
Qsf(t)==CSP_Qin(t)-CSP_Qout(t)+CSP_SU(t)+CSP_Gen(t),​%% IGDT新增约束​
​HeatLoad(t)==(1-0.2*alfa)*HeatLoads(t),%热负荷鲁棒区间约束
​EleLoad(t)==(1-0.3*alfa)*EleLoads(t),%电负荷鲁棒区间约束
​P_v_pre(t)==(1+0.1)*P_v_pres(t),%光伏鲁棒区间约束
​P_w_pre(t)==(1+0.1)*P_w_pres(t),%风电鲁棒区间约束
​​gasLoad(t)==(1-0.3*alfa)*gasLoads(t),%气负荷鲁棒区间约];
%% 不确定性系数加权，各取0.2（此概率可自行设置，加一起等于1即可）​P_yun==sum(gamma_gas.*Gas)+sum(0.1*PV_P)+sum(0.1*WP_P)+sum(0.1*GT_P)+sum(0.1*GB_Q)+sum(gamma_buy.*(P_buy+P2G))+sum(0.1*CSP_GenP),C_CO2==0.5*(0.35*sum(GB_Q)+sum(C_GT)+1.08*sum(P_buy)-sum(G_P2G)),​cost<=29898.4065*(1-0.13),%设置目标函数约束，0.3为偏差系数，不过取的过小，否则容易无解；​   

部分内容源自网络，侵权联系删除！

欢迎感兴趣的小伙伴点关注并私信获取完整版代码，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！