Problem: 1143. 最长公共子序列

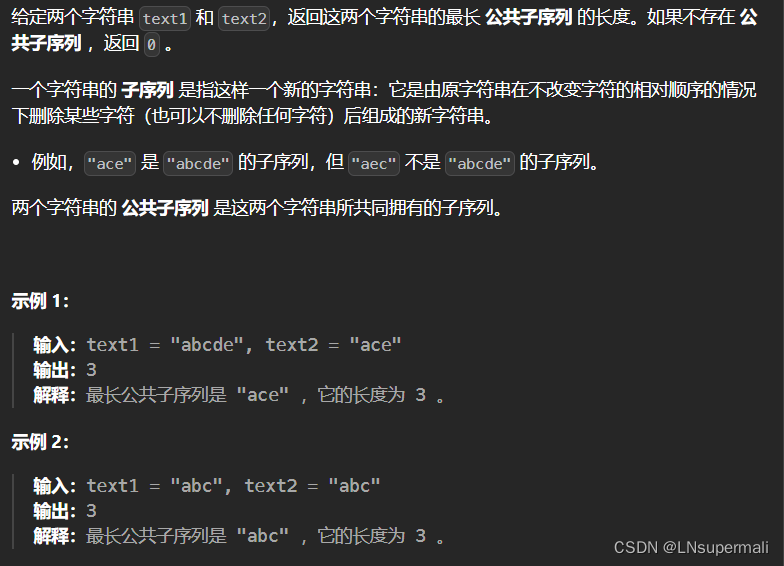
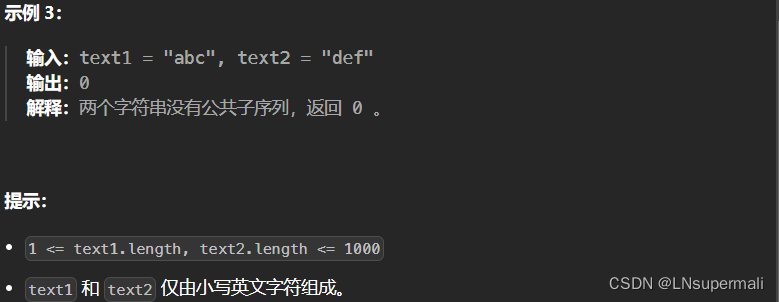
题目描述

思路

我们统一标记：str1[i]代表text1表示的字符数组，str2[j]代表text2表示的字符数组；LCS代表最长的公共子序列；（我们易得只有str1[i]和str2[j]均在LCS中时才能说明str1[i]和str2[j]是LCS的一部分）

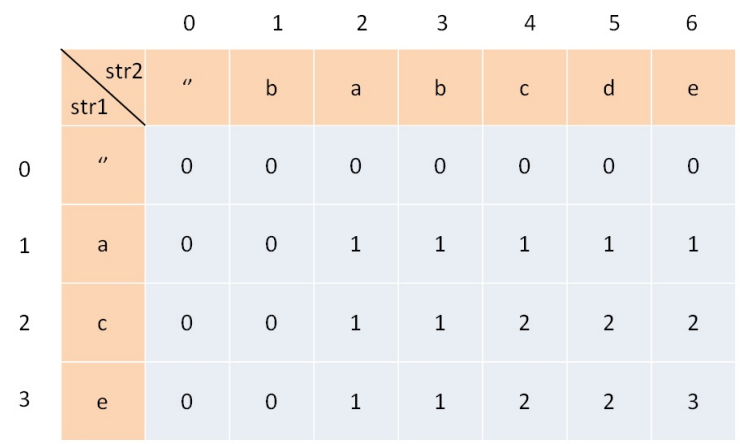
1.状态定义：dp[i][j]代表str1[1~i]和str2[1 ~ j]的最长公共子序列（我们暂时认为索引是从 1 开始的，例如：d[2][4] 的含义就是：对于 “ac” 和 “babc” ，它们的LCS ⻓度是 2）

2.状态转移：

2.1:初始状态初始化：我们初始化dp[0][j] = 0; dp[i][0] = 0,逻辑上说明，当str1或者str2其中为空时则LCS为0；
2.2:状态转移：若*str1[i] == str2[j]则dp[i][j] = dp[i - 1][j - 1] + 1;若str1[i] != str2[j]*则dp[i][j] == max(dp[i-1][j],dp[i][j-1])

补充：

当*str1[i] != str2[j]*实则有三种状态：str1[i] != LCS[i];str2[j] != LCS[j]; str1[i] != str2[i] != LCS[i];但是我们在状态转移方程中dp[i][j] == max(dp[i-1][j],dp[i][j-1]);
实际上dp[i][j] == max(dp[i-1][j],dp[i][j-1]，dp[i - 1][j - 1]),但是回看dp[i][j]的定义我们易知dp[i - 1][j - 1]是一定小于dp[i-1][j]和dp[i][j-1],所以我们则直接求取**max(dp[i-1][j],dp[i][j-1])**即可

复杂度

时间复杂度:

$O(M\times N)$;其中$M$为text1的长度，$N$为text2的长度

空间复杂度:

$O(M\times N)$

Code

class Solution {
public:/*** Find the longest common subsequence* @param text1 Given string* @param text2 Given string* @return int*/int longestCommonSubsequence(string text1, string text2) {int len1 = text1.length();int len2 = text2.length();//DP arrayvector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));//for (int i = 1; i < len1 + 1; ++i) {for (int j = 1; j < len2 + 1; ++j) {if (text1.at(i - 1) == text2.at(j - 1)) {dp[i][j] = 1 + dp[i - 1][j - 1];} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[len1][len2];}
};