如何用Python检查时间序列数据是否平稳？

时间序列数据通常以其时间性质为特征。这种时间性质为数据增加了趋势或季节性，使其与时间序列分析和预测兼容。如果时间序列数据不随时间变化或没有时间结构，则称其为静态数据。因此，检查数据是否平稳是非常必要的。在时间序列预测中，如果数据是平稳的，我们就无法从数据中获得有价值的见解。

静态数据的示例图：

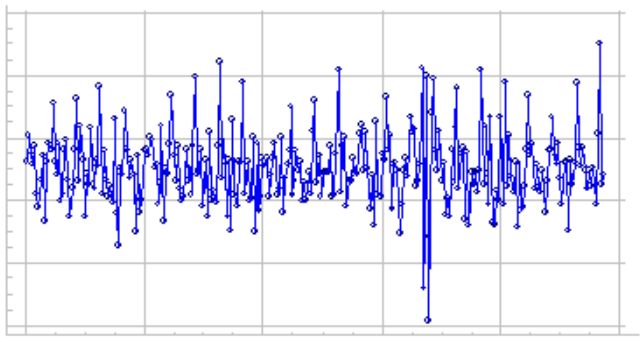
在这里插入图片描述

平稳性的类型

当涉及到识别数据是否是平稳的时，这意味着识别数据中平稳性的细粒度概念。在时间序列数据中观察到的平稳性类型包括：

趋势平稳：不显示趋势的时间序列。
季节性平稳（Seasonal Stationary）：不显示季节性变化的时间序列。
严格平稳：观测值的联合分布不随时间变化。

实现方法及步骤

下面的步骤将让用户容易地理解检查给定时间序列数据是否平稳的方法。

步骤1：绘制时间序列数据

# import python pandas library
import pandas as pd# import python matplotlib library for plotting
import matplotlib.pyplot as plt# read the dataset using pandas read_csv() 
# function
data = pd.read_csv("daily-total-female-births-IN.csv",header=0, index_col=0)# use simple line plot to see the distribution 
# of the data
plt.plot(data)

输出
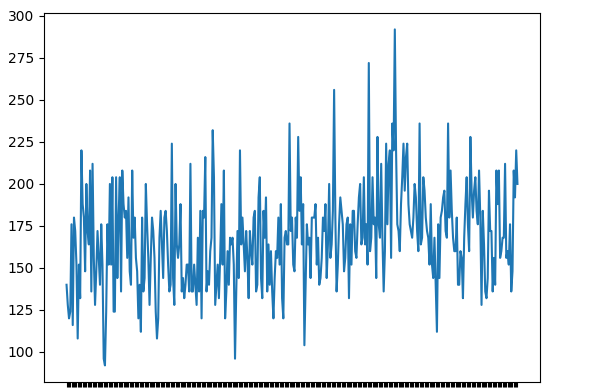
在这里插入图片描述
步骤2：评估描述性统计量

这通常是通过将数据分成两个或多个分区并计算每组的均值和方差来完成的。如果这些一阶矩在这些分区之间是一致的，那么我们可以假设数据是平稳的。让我们使用1949 - 1960年之间的航空公司乘客计数数据集。

# import python pandas library
import pandas as pd# import python matplotlib library for
# plotting
import matplotlib.pyplot as plt# read the dataset using pandas read_csv() 
# function
data = pd.read_csv("AirPassengers.csv",header=0, index_col=0)# print the first 6 rows of data
print(data.head(10))# use simple line plot to understand the 
# data distribution
plt.plot(data)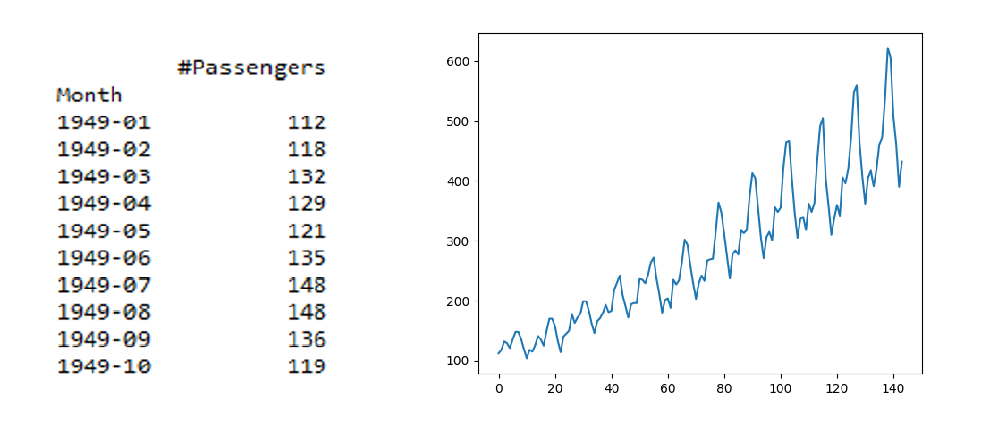

在这里插入图片描述
现在，让我们将这些数据划分为不同的组，计算不同组的均值和方差，并检查一致性。

# import the python pandas library
import pandas as pd# use pandas read_csv() function to read the dataset.
data = pd.read_csv("AirPassengers.csv", header=0, index_col=0)# extracting only the air passengers count from
# the dataset using values function
values = data.values# getting the count to split the dataset into 3
parts = int(len(values)/3)# splitting the data into three parts
part_1, part_2, part_3 = values[0:parts], values[parts:(parts*2)], values[(parts*2):(parts*3)]# calculating the mean of the separated three 
# parts of data individually.
mean_1, mean_2, mean_3 = part_1.mean(), part_2.mean(), part_3.mean()# calculating the variance of the separated 
# three parts of data individually.
var_1, var_2, var_3 = part_1.var(), part_2.var(), part_3.var()# printing the mean of three groups
print('mean1=%f, mean2=%f, mean2=%f' % (mean_1, mean_2, mean_3))# printing the variance of three groups
print('variance1=%f, variance2=%f, variance2=%f' % (var_1, var_2, var_3))

输出
在这里插入图片描述
输出清楚地表明，三组的平均值和方差彼此差异很大，说明数据是非平稳的。例如，如果平均值mean_1 = 150，mean_2 = 160，mean_3 = 155和variance_1 = 33，variance_2 = 35，variance_3 = 37，那么我们可以得出结论，数据是平稳的。有时这种方法可能会对某些分布失败，如对数范数分布。

让我们尝试与上面相同的示例，但使用NumPy的log（）函数获取乘客计数的日志并检查结果。

# import python pandas library
import pandas as pd# import python matplotlib library for plotting
import matplotlib.pyplot as plt# import python numpy library
import numpy as np# read the dataset using pandas read_csv()
# function
data = pd.read_csv("AirPassengers.csv", header=0, index_col=0)# extracting only the air passengers count 
# from the dataset using values function
values = log(data.values)# printing the first 15 passenger count values
print(values[0:15])# using simple line plot to understand the 
# data distribution
plt.plot(values)

输出
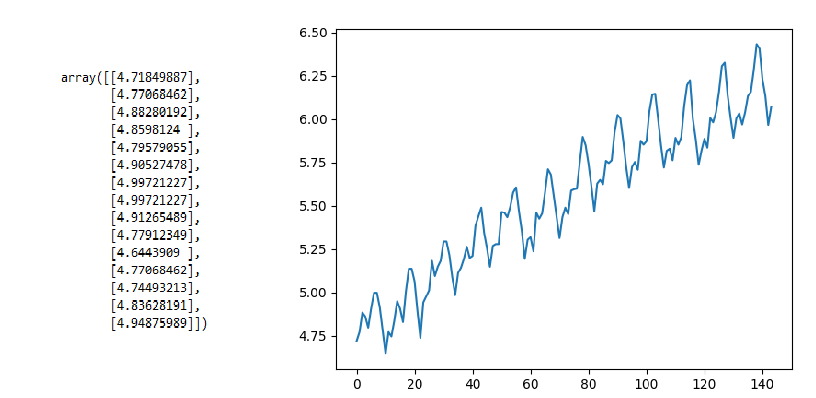
在这里插入图片描述
输出表示有一些趋势，但不像前面的情况那样非常陡峭，现在让我们计算分区均值和方差。

# getting the count to split the dataset
# into 3 parts
parts = int(len(values)/3)# splitting the data into three parts.
part_1, part_2, part_3 = values[0:parts], values[parts:(parts*2)], values[(parts*2):(parts*3)]# calculating the mean of the separated three 
# parts of data individually.
mean_1, mean_2, mean_3 = part_1.mean(), part_2.mean(), part_3.mean()# calculating the variance of the separated three 
# parts of data individually.
var_1, var_2, var_3 = part_1.var(), part_2.var(), part_3.var()# printing the mean of three groups
print('mean1=%f, mean2=%f, mean2=%f' % (mean_1, mean_2, mean_3))# printing the variance of three groups
print('variance1=%f, variance2=%f, variance2=%f' % (var_1, var_2, var_3))

输出
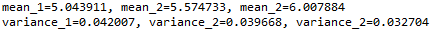
在这里插入图片描述
理想情况下，我们会期望均值和方差非常不同，但它们是相同的，在这种情况下，这种方法可能会非常失败。为了避免这种情况，我们有另一个统计测试，下面讨论。

步骤3：增强的Dickey-Fuller检验

这是一个统计测试，专门用于测试单变量时间序列数据是否平稳。这个测试是基于一个假设，可以告诉我们它可以被接受的概率程度。它通常被归类为单位根检验之一，它决定了一个单变量时间序列数据遵循趋势的强度。我们来定义零假设和替代假设，

Ho（假设）：时间序列数据是非平稳的
H1（替代假设）：时间序列数据是平稳的

假设α = 0.05，表示（95%置信度）。如果p > 0.05不能拒绝零假设，则用p值解释检验结果，否则如果p <= 0.05则拒绝零假设。现在，让我们使用相同的航空乘客数据集，并使用stats model包提供的adfuller（）统计函数对其进行测试，以检查数据是否稳定。

# import python pandas package
import pandas as pd# import the adfuller function from statsmodel 
# package to perform ADF test
from statsmodels.tsa.stattools import adfuller# read the dataset using pandas read_csv() function
data = pd.read_csv("AirPassengers.csv", header=0, index_col=0)# extracting only the passengers count using values function
values = data.values# passing the extracted passengers count to adfuller function.
# result of adfuller function is stored in a res variable
res = adfuller(values)# Printing the statistical result of the adfuller test
print('Augmneted Dickey_fuller Statistic: %f' % res[0])
print('p-value: %f' % res[1])# printing the critical values at different alpha levels.
print('critical values at different levels:')
for k, v in res[4].items():print('\t%s: %.3f' % (k, v))

输出
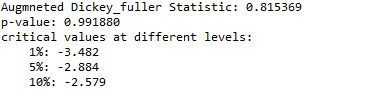
在这里插入图片描述
根据我们的假设，ADF统计量远远大于不同水平的临界值，并且p值也大于0.05，这意味着我们无法在90%，95%和99%的置信度下拒绝零假设，这意味着时间序列数据是强非平稳的。

现在，让我们尝试对log normed值运行ADF测试，并交叉检查我们的结果。

# import python pandas package
import pandas as pd# import the adfuller function from statsmodel
# package to perform ADF test
from statsmodels.tsa.stattools import adfuller# import python numpy package
import numpy as np# read the dataset using pandas read_csv() function
data = pd.read_csv("AirPassengers.csv", header=0, index_col=0)# extracting only the passengers count using 
# values function and applying log transform on it.
values = log(data.values)# passing the extracted passengers count to adfuller function.
# result of adfuller function is stored in a res variable
res = adfuller(values)# Printing the statistical result of the adfuller test
print('Augmneted Dickey_fuller Statistic: %f' % res[0])
print('p-value: %f' % res[1])# printing the critical values at different alpha levels.
print('critical values at different levels:')
for k, v in res[4].items():print('\t%s: %.3f' % (k, v))