文章目录
- 0. Contents
- 1. Multi-Agent Path Finding (MAPF)
- 1.1 HCA*
- 1.2 Single-Agent A*
- 1.3 ID
- 1.4 M*
- 1.5 Conflict-Based Search(CBS)
- 1.6 ECBS
- 1.6.1 heuristics
- 1.6.2 Focal Search
- 2. Velocity Obstacle (VO,速度障碍物)
- 2.1 VO
- 2.2. RVO
- 2.3 ORCA
- 3. Flocking model(群落模型)
- 4. Trajectory Planning for Swarms(集群轨迹规划)
- 4.1 Background
- 4.2 Methods
- 4.2.1 Search/Sampling Based
- 4.2.2 Optimization Based
- 4.2.2.1 Formulation
- 4.2.2.2 Solving
- 5. Formation(编队)
- 5.1 Preliminary
- 5.2 Consensus-based Control(基于共识的控制)
- 5.3 Potential Field
- 5.4 Shape Vector
- 5.5 Formation Rearrangement
- 5.6 Similarity Metric(相似性度量)
- 6. Summary
- X. Reference
0. Contents

1. Multi-Agent Path Finding (MAPF)
本节主要讲解多智能体路径规划,转化为图搜索问题进行求解。

主要是考虑固定节点和图上的路径规划问题。
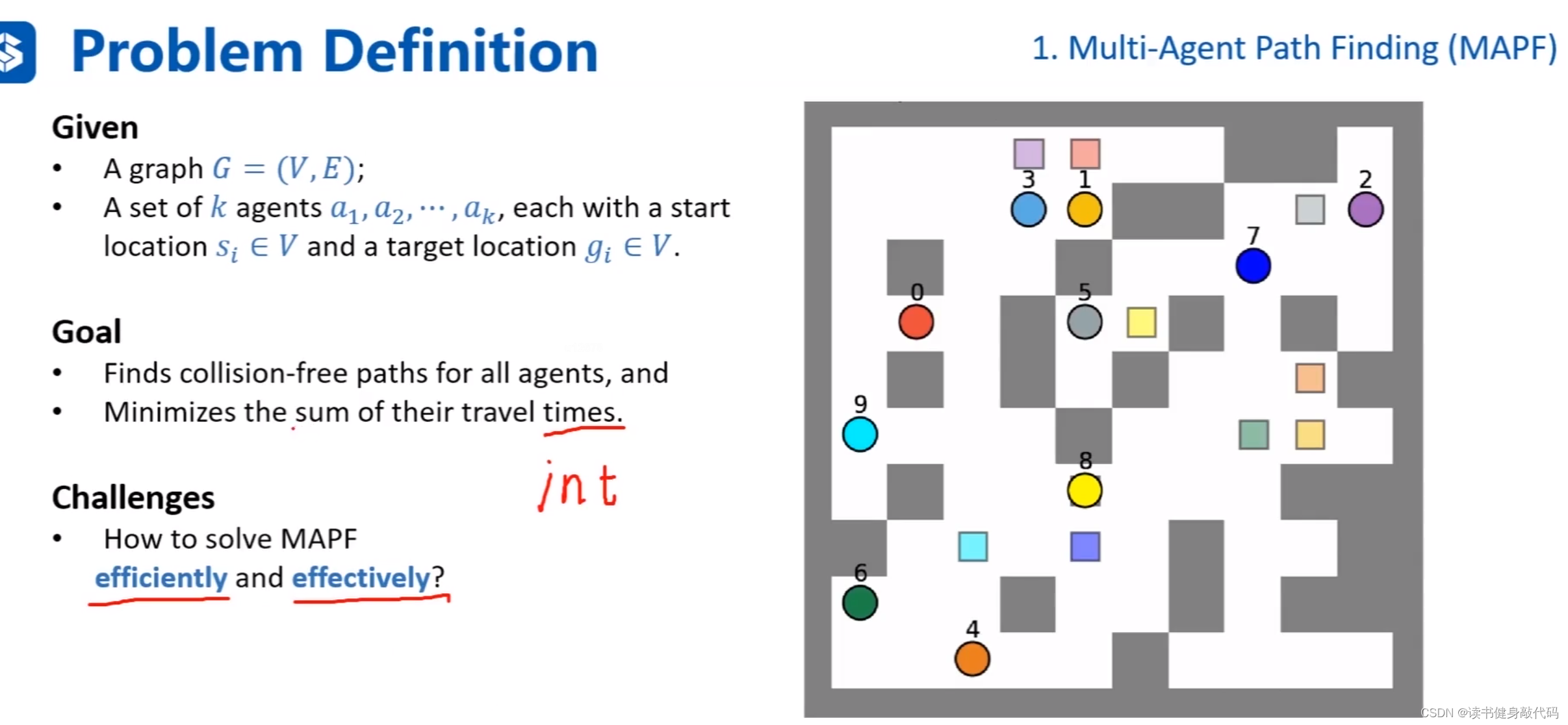
课程中的agents和robotics所指相同。
Givens:一张地图和图上的节点。
Goal:寻找到所有agents的路径,并且最小化cost
times指的就是cost,如果是one-unit grid map,则这种times一般是整数,如果类似于或者时刻表规划,则可能是double。
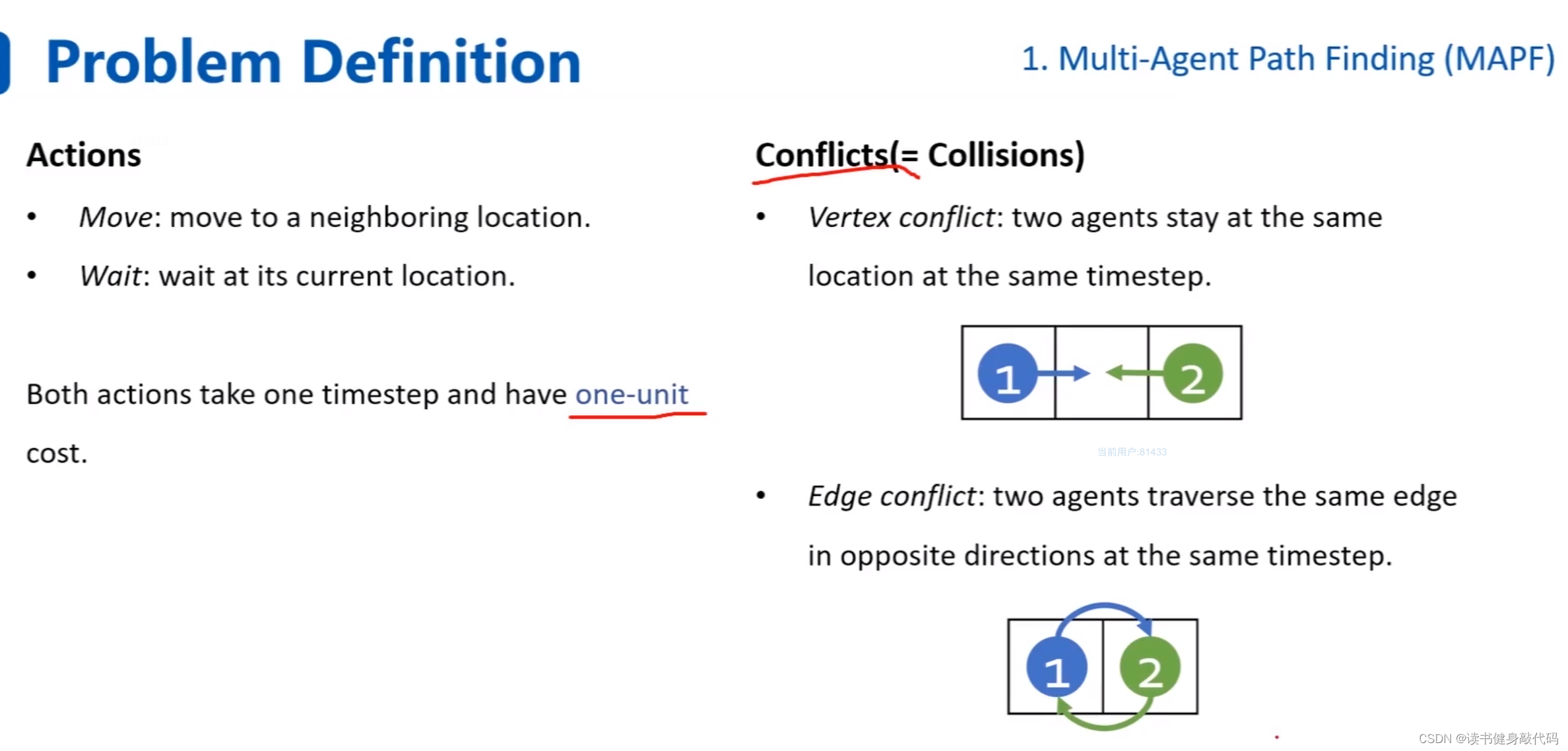
定义动作:移动,等待。
冲突:1. 顶点冲突同时想进入同一个grid,2. 边冲突:两个agents同时以相反的方向通过同一条边。(即想交换位置)。
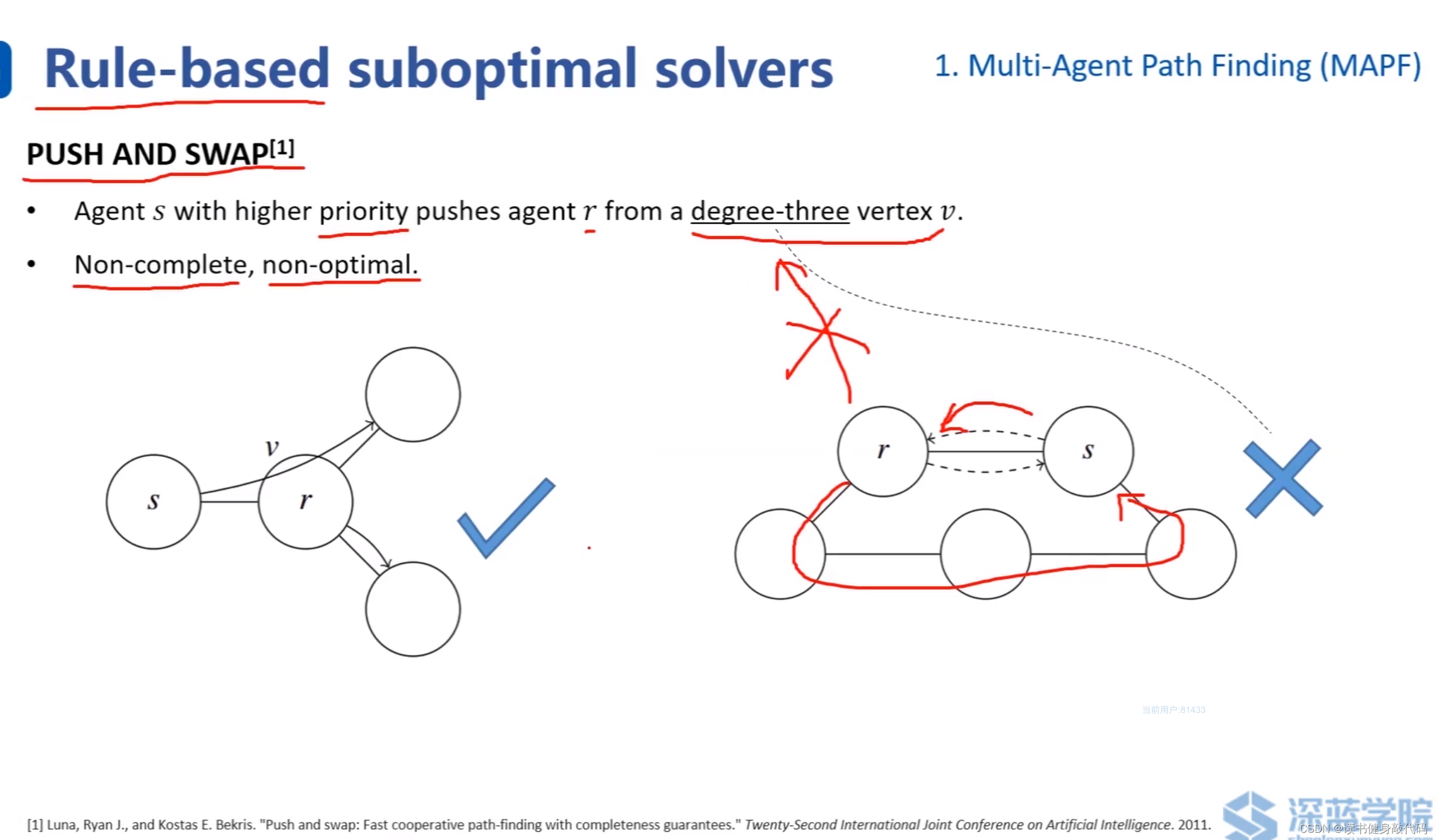
一些人工定义的规则:
最著名的是:push and swap, ref[1]
push:优先级高的可以推开优先级低的节点,低的节点度必须 ≥ 3 \geq 3 ≥3(即连接低优先级的边不少于3条)。上左 s s s优先级高于 r r r,要去右上角的节点,可以把r往右下推开,然后经过 r r r的原有位置,到达右上。
人工定义的规则较难适应真实的复杂场景,会出现non-complete(找不到解)和non-optimal(解不是最优)的情况。
complete:如果解存在,那么一定可以找到一个解。
optimal:如果有多个解存在,可以找到全局cost最低的那个。
1.1 HCA*
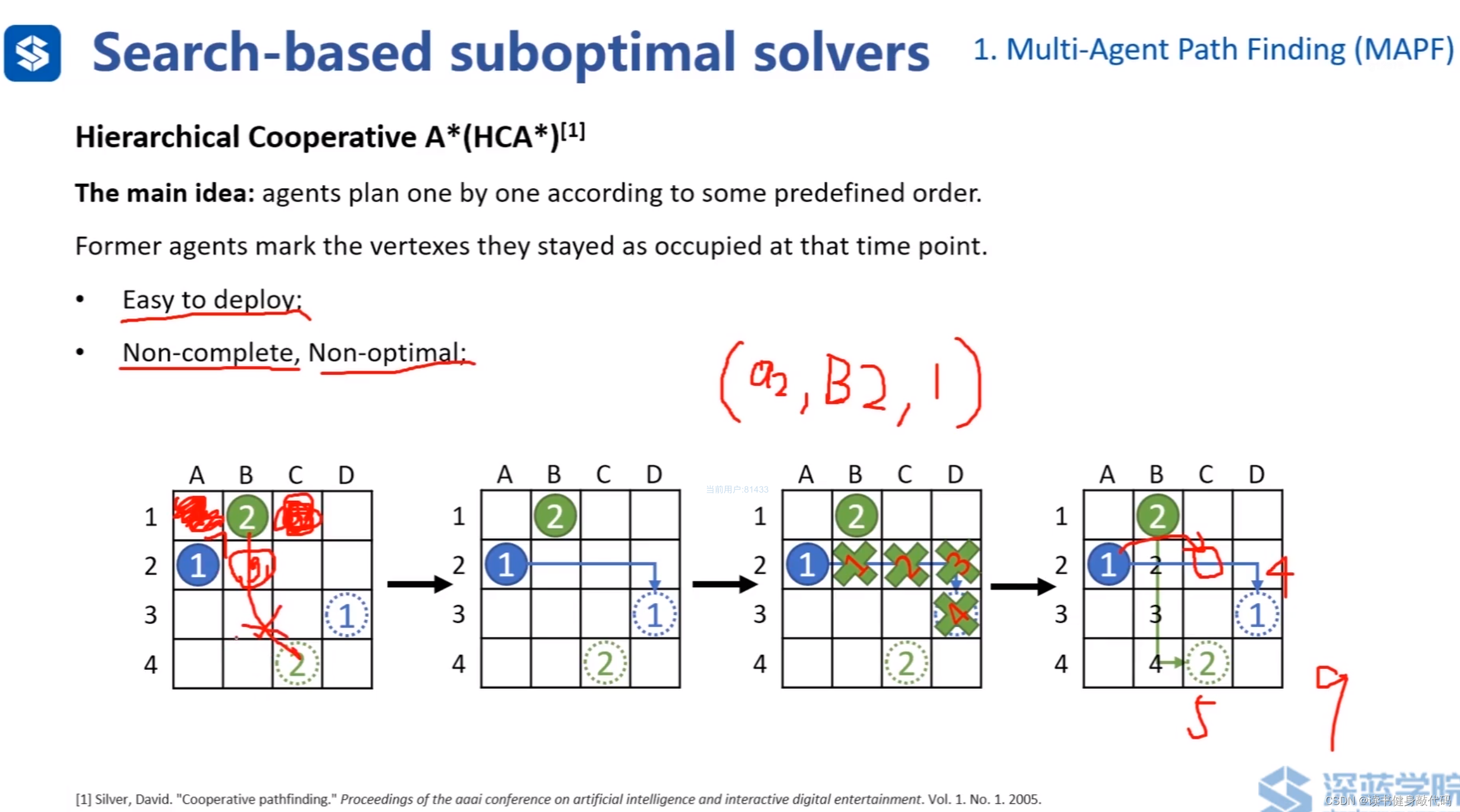
基于搜索的suboptimal solvers:HCA*(层次化合作A*),ref[2]。
高优先级agent在规划时无需考虑低优先级的agent,反之,低优先级在规划时需要考虑高优先级agent的存在。
上图①比②优先级高,①先规划出路径,为了避免碰撞,①的路径在②在规划时对②产生了如第3个图所示的约束,分别表示②在第1,2,3,4时刻不能在该处,以第1时刻的约束为例: ( a 2 , B 2 , 1 ) (a_2,B_2,1) (a2,B2,1)代表是对 a g e n t 2 agent_2 agent2的,在 B _ 2 B\_2 B_2格子的,在1时刻的约束。该表示法后面会用到。
上例最终时间cost:①4单位+②5单位=9单位
HCA* pros:容易实施,在传统A*的collision check中添加对其他agent的判断即可。
cons:Non-complete, Non-optimal。如上第1个图所示,若②左右均为障碍物,在第1时刻,①位于 B _ 2 B\_2 B_2格子,此时②找不到解,所以non-complete。
1.2 Single-Agent A*
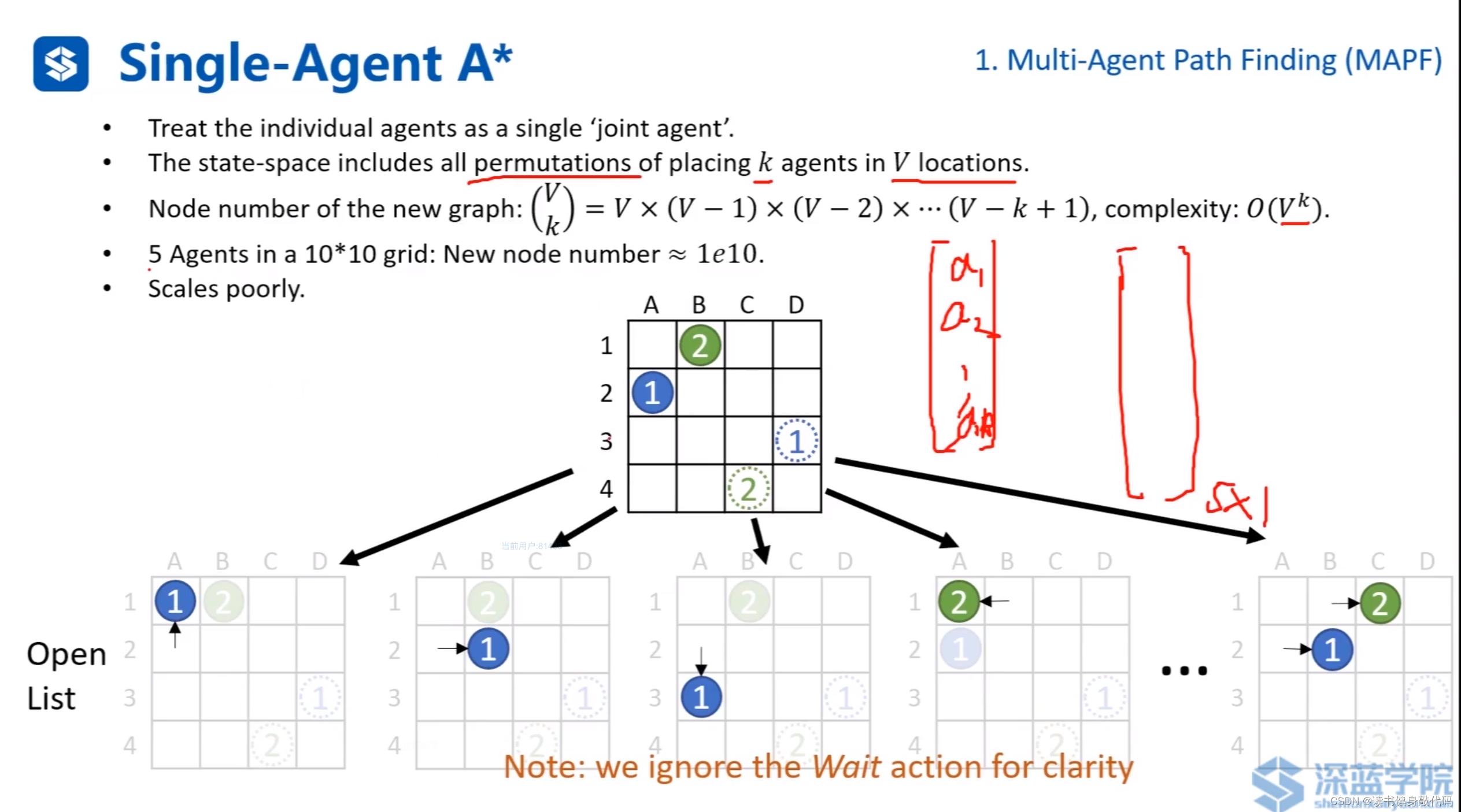
基于A* 的更加完备和最优的算法:Single-Agent A*。
把每个agent看做一个联合agent,构造k个agents的V个位置的状态空间的排列组合,复杂度为 O ( V k ) O(V^k) O(Vk),比如:①往任一可行方向单独移动一格为一个状态,②也是,①②同时往任一方向移动一格也是一个状态…对所有agent都使用这样的排列组合,最终构成大向量。
显然这种方法复杂度非常高,大规模问题无法使用。
1.3 ID

ref[3] 每个agent当做一个单独的group,各自找自己的最优路径,如果发生碰撞,尝试找相同cost的不碰撞的path,如果找不到,则将发生碰撞的两个agents则合并为一个group,然后使用Single-Agent A*。
ID算法的思想和之前PRM的lazy collision checking有些类似,先搜出一条path,然后对path进行collision checking。
Independence Detection (ID)仍然是完备且最优的。
1.4 M*
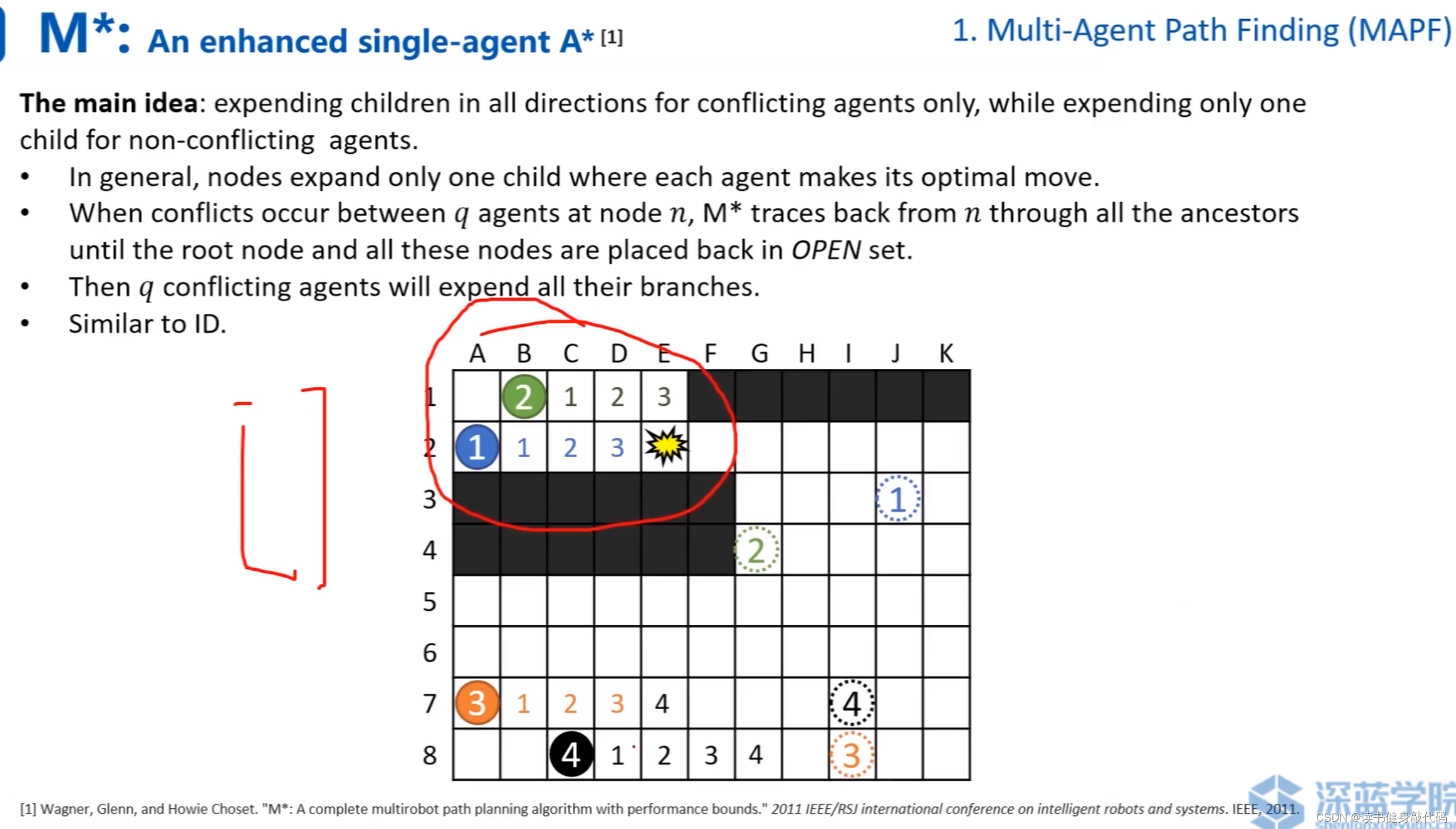
M*(ref [4])相对于ID的改进:在每个group单独进行搜索时,边搜边进行collision checking,发现collision时,将group进行合并。
1.5 Conflict-Based Search(CBS)
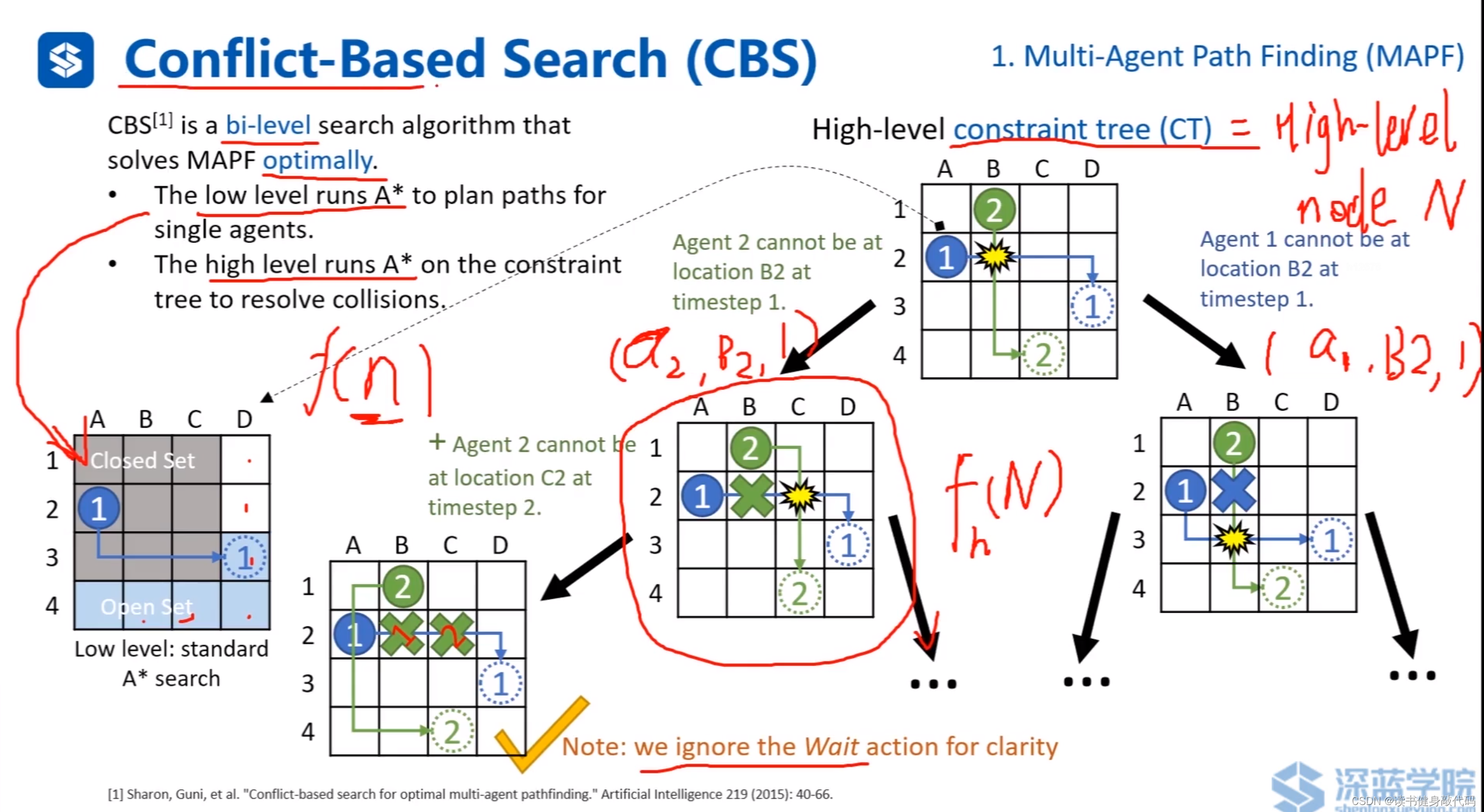
CBS是双层次的A*(ref [5]),low level A*对每个agent进行搜索,遇到conflict时,进行high level的搜索,让碰撞的两个agent分别通过碰撞点,衍生出两个case,在两个case中继续进行拓展,重复此步骤,如此产生的树结构称为constaint tree(CT)。
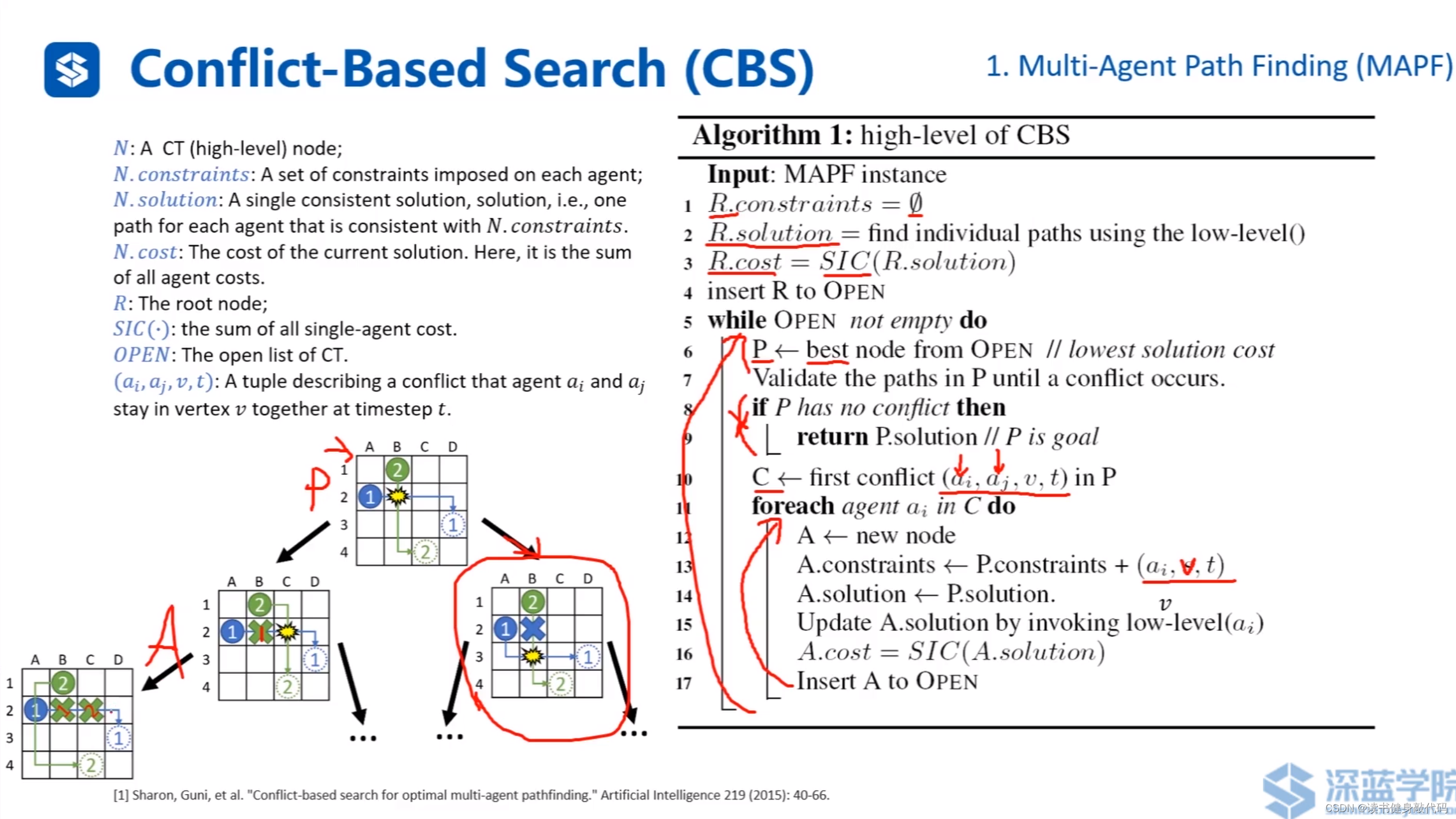
CBS的具体算法流程。
R R R:根节点,开始时约束为空。
对所有agent进行low-level的A*
算出当前的cost
把 R R R insert 到open-set中
while open-set非空:
在open-set中找cost最低的node
如果发生碰撞且所有agent均到达自己的目标节点,
返回 目标节点。
如果在P中是首次碰撞,则加入到碰撞集中
遍历碰撞集每个agnet:
分别对另一个agent施加约束,并对其进行low-level A*,更新cost,并加入到open-set中
1.6 ECBS

上面讲的方法均可以归类到optimal solvers或suboptimal solvers中,在二者中间还存在一种bounded suboptimal solvers,它的cost不是最优的 C ∗ C^* C∗,但是小于其上界 ω C ∗ ( ω > 1 ) \omega C^*(\omega>1) ωC∗(ω>1)。接下来讲解一种方法:ECBS。而BCBS更多的意义是为了推导ECBS。
1.6.1 heuristics
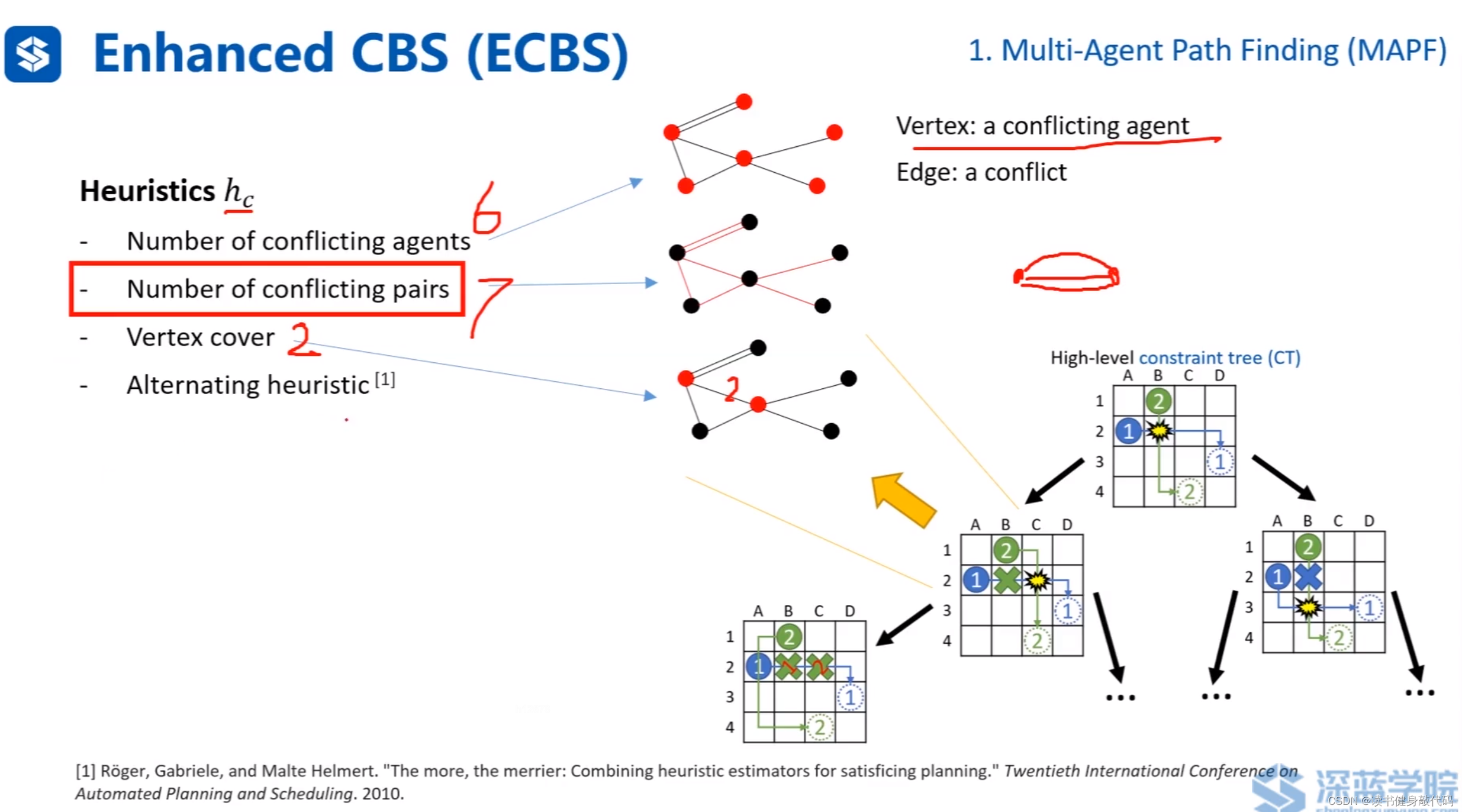
与A* 中构造heuristic的构造方式不同,这里引入碰撞图的概念,
碰撞图中,每个节点代表发生碰撞的agent,每条边代表这两个agent发生了一次碰撞。
有几种heuristics(ref[6]):
- 发生碰撞的agents的数量(上例为6)
- 碰撞的次数(边的条数,上例为7)
- vertex cover:碰撞图中的每个节点都至少与选择的节点有连接边(上例为2个)
- 上面几种heuristics交替使用
1.6.2 Focal Search
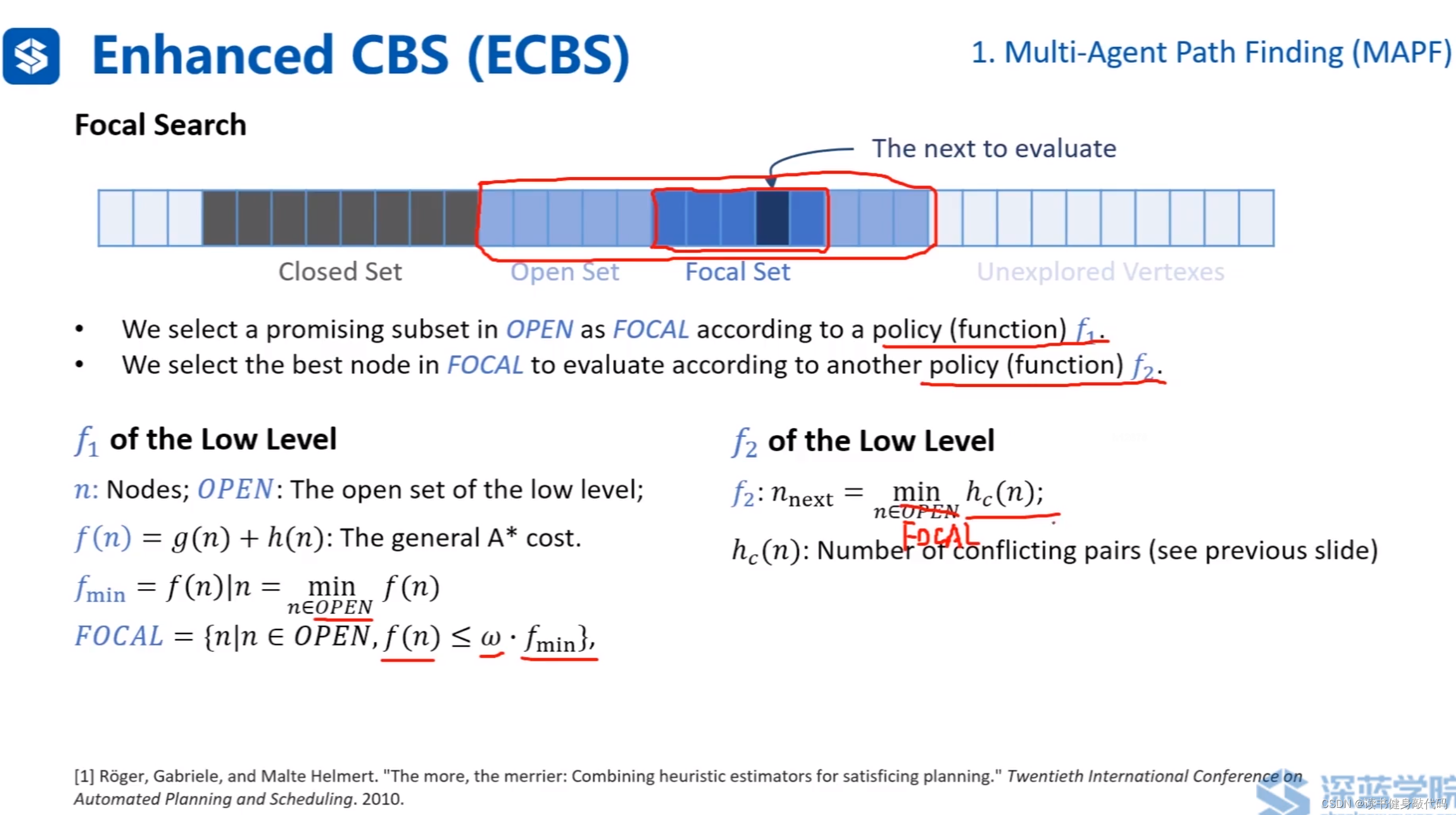

在open set中利用policy function f 1 f_1 f1(一个规则)选择一个子集Focal set,再使用policy function f 2 f_2 f2(另一个规则)选择一个node进行下一次evaluate。(对应到A*中,在open set中直接选择cost最小的进行evaluate,这里定义了两个选择规则)。
分low-level和high-level讲解:
- low-level的选取:
f 1 \bm{f_1} f1:按照A*算法 f = g + h f=g+h f=g+h计算 f f f,在open set中取 f f f最小的node对应的cost f m i n f_{min} fmin,将open set中cost小于 ω f m i n \omega f_{min} ωfmin的node取出来,作为FOCAL集。
f 2 \bm{f_2} f2:在FOCAL集内,按照1.6.1节选取的heuristics方法计算heuristics h c ( n ) h_c(n) hc(n)
- high-level选取:
high-level就是针对发生碰撞的nodes组成的group。
f 1 \bm{f_1} f1:由于high-level每个node对应很多agent,每个node都有自己的 f m i n f_{min} fmin。
对每个node内的所有agent的 f m i n f_{min} fmin求和, L B LB LB指和最小的high-level的node, L B ( N ) LB(N) LB(N)是对应的最小和。
high-level的FOCAL就是open-set中满足 N . c o s t ≤ ω L B N.cost\leq \omega \bm{LB} N.cost≤ωLB的所有high-level node。
f 2 \bm{f_2} f2:在high-level的FOCAL中取heuristics最小的high-level node。
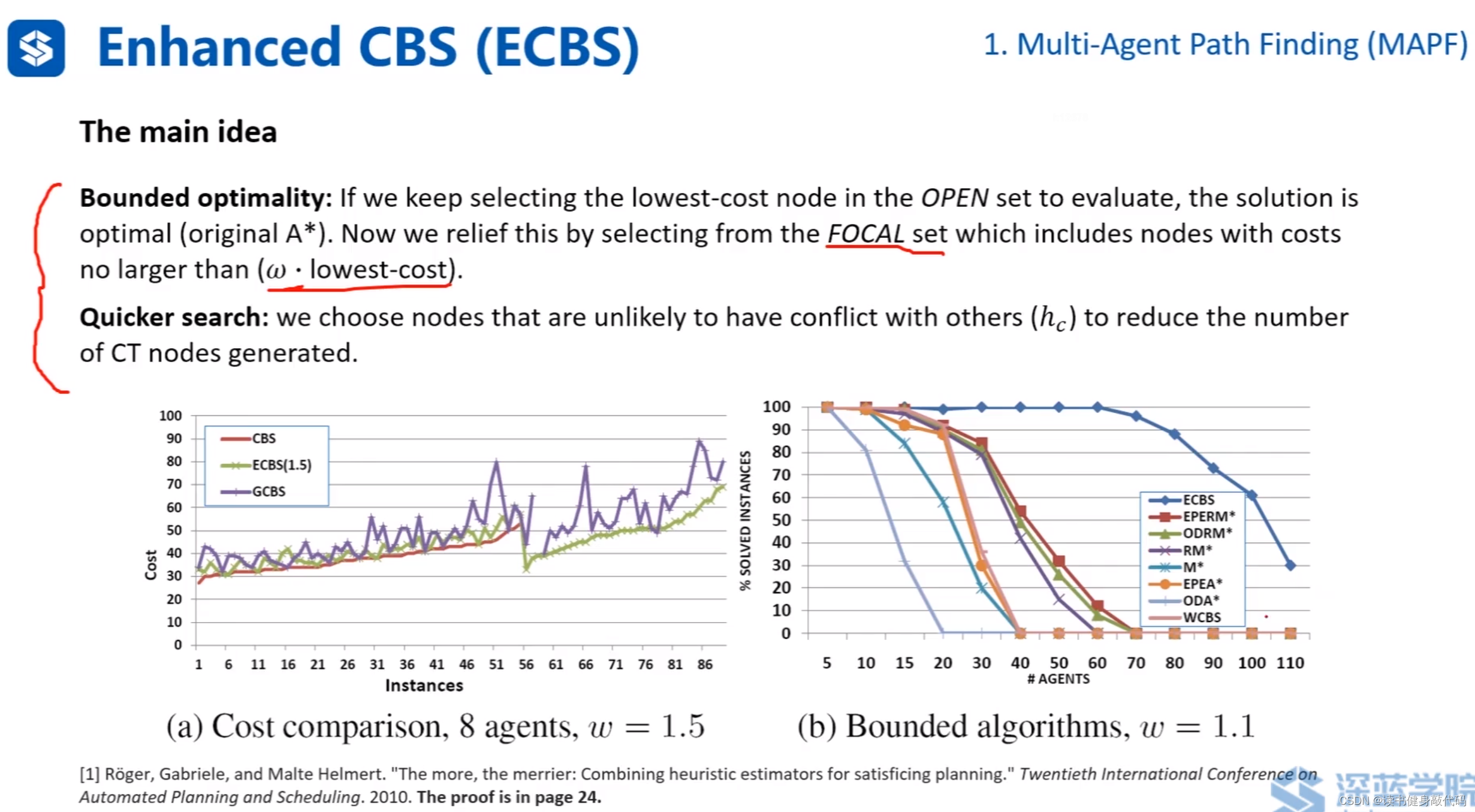
ECBS的main idea:
- relief搜索的条件,不仅仅找 f m i n f_{min} fmin的node,而是以 f m i n f_{min} fmin框定一个范围,在该范围内搜索能保证bounded optimality.
- 在FOCAL中进行扩展,由于选择的是碰撞较少的节点进行扩展,缩小了扩展节点所带来的新的碰撞节点的产生,降低了潜在扩展次数,加快了搜索。
实验表明ECBS的cost和CBS(最优)的cost较为接近,且搜索较快。
2. Velocity Obstacle (VO,速度障碍物)
2.1 VO
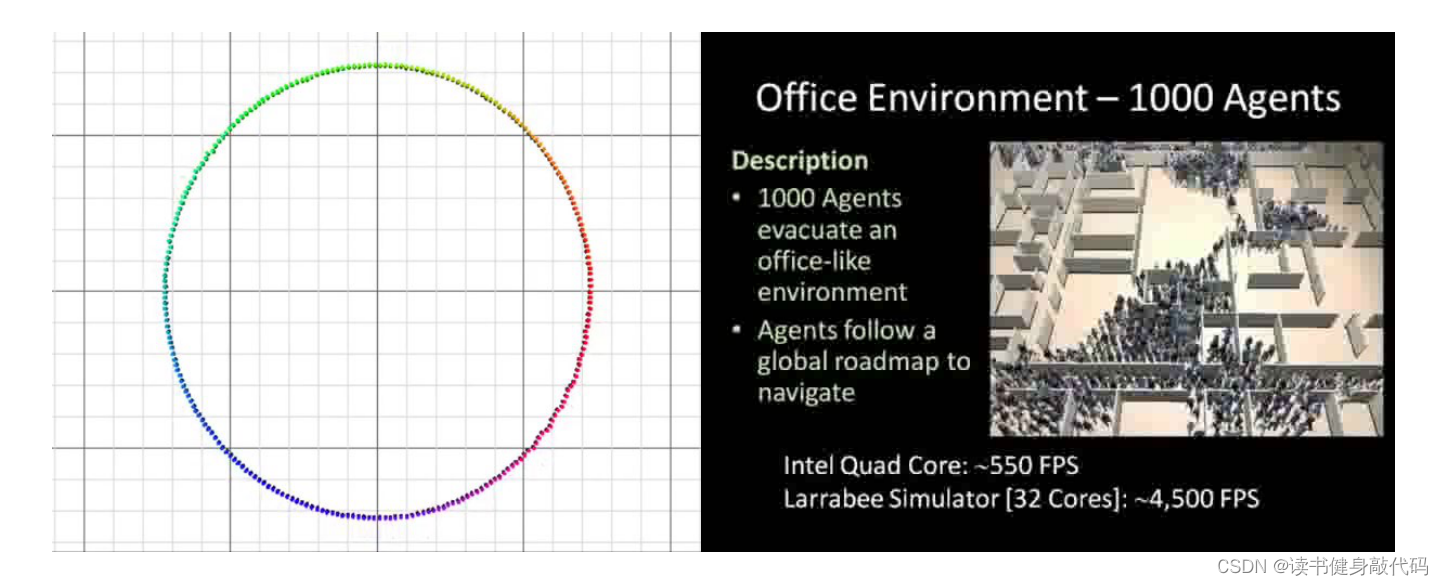
VO的仿真实验:智能体排成圆和1000个智能体从办公室场景撤退。

上个世纪提出VO(ref[7]),后来RVO(ref[8]),ORCA(ref[9])对VO进行了改进。
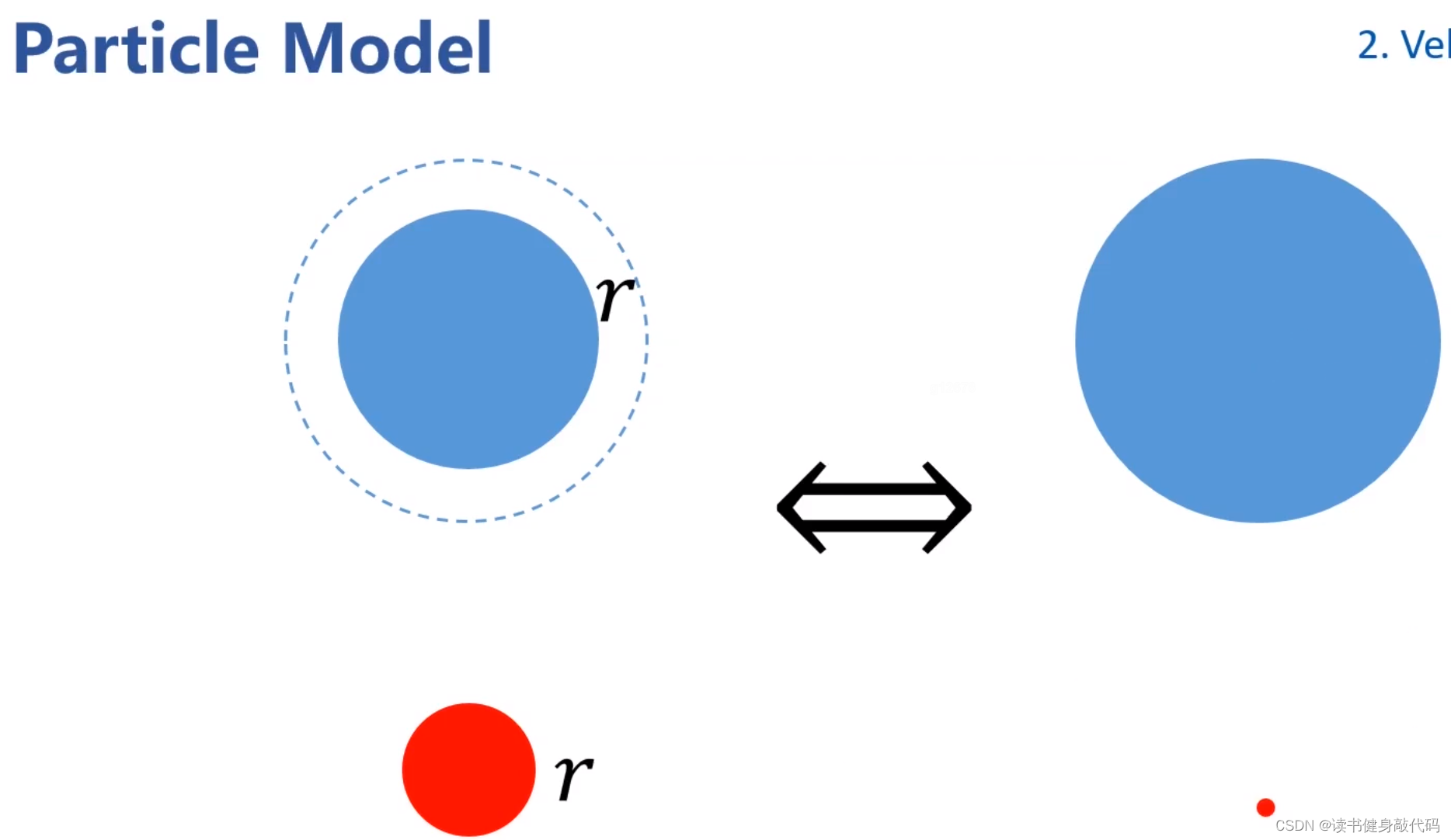
将机器人质点化,对障碍物进行膨胀。
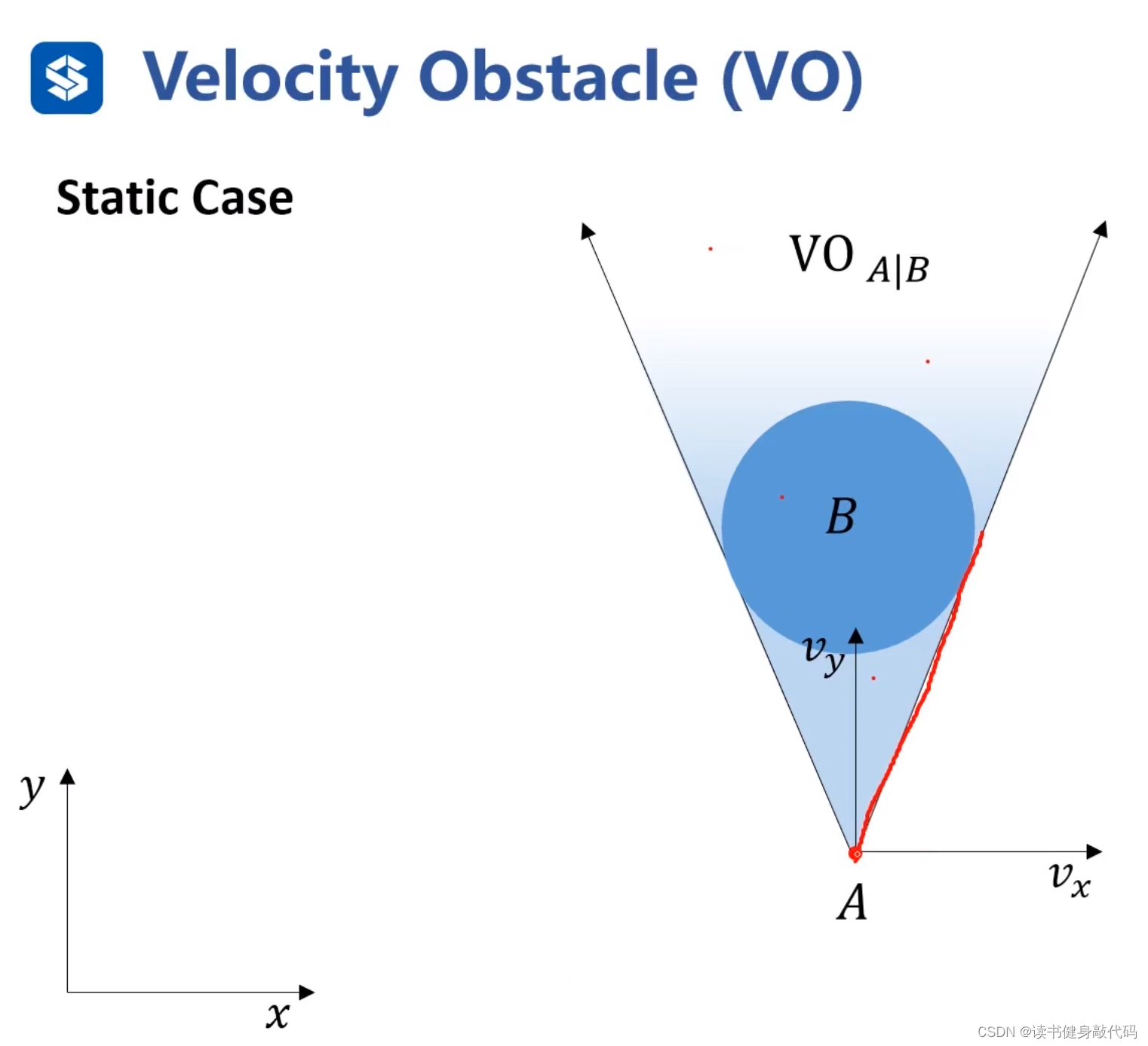
静态情况(障碍物不动):
速度取在扇形区域内时会撞到障碍物,所以扇形区域就是VO。 V O A ∣ B VO_{A|B} VOA∣B是 B B B相对于 A A A的速度障碍物。VO区域是定义在速度空间内的区域,在该区域内的速度会撞到障碍物。速度空间的障碍物,所以叫速度障碍物。速度坐标系和位置坐标系是画在同一个平面的,速度坐标系的原点是agent所处的位置,而位置坐标系原点不一定与速度坐标系相同。
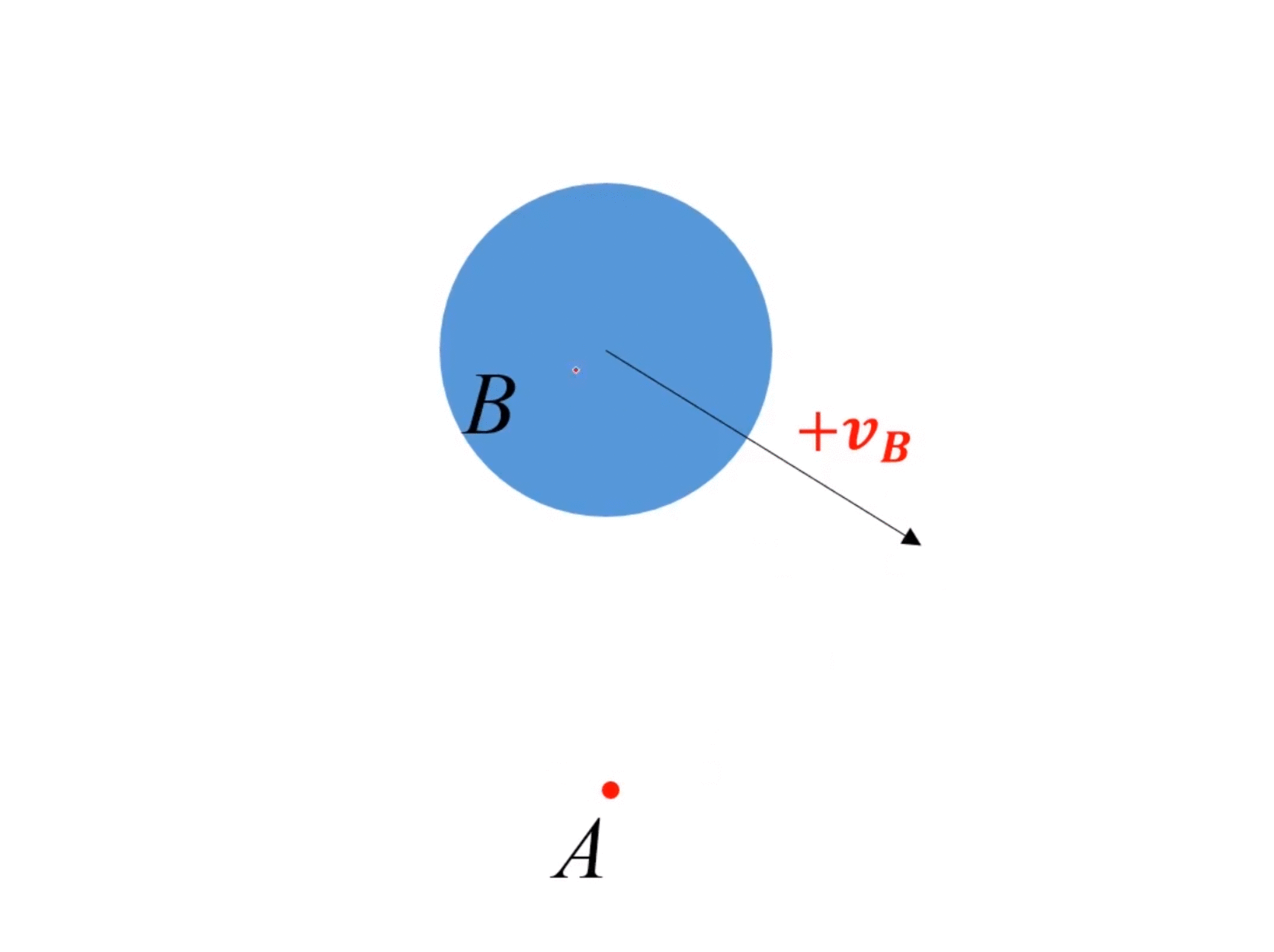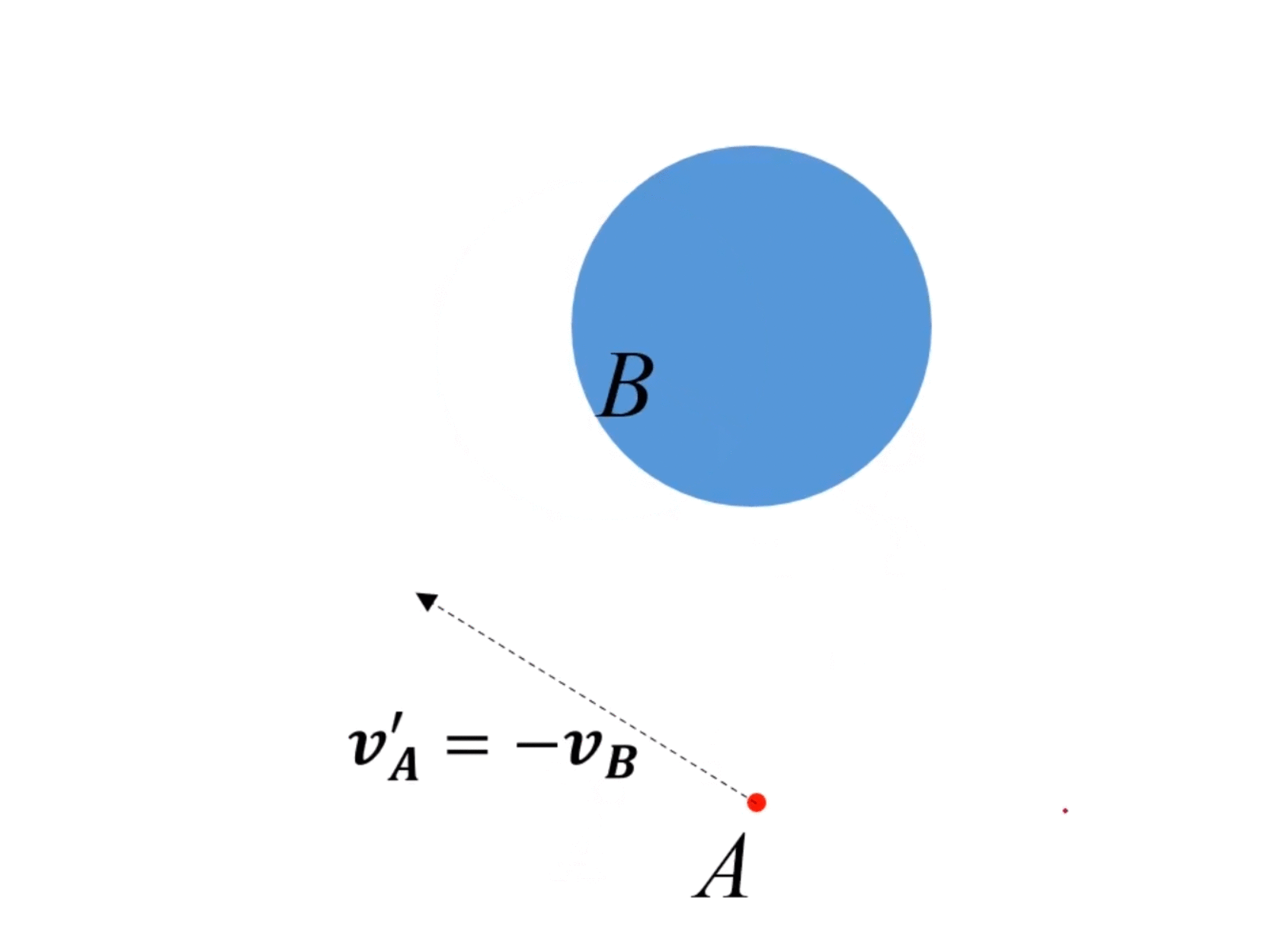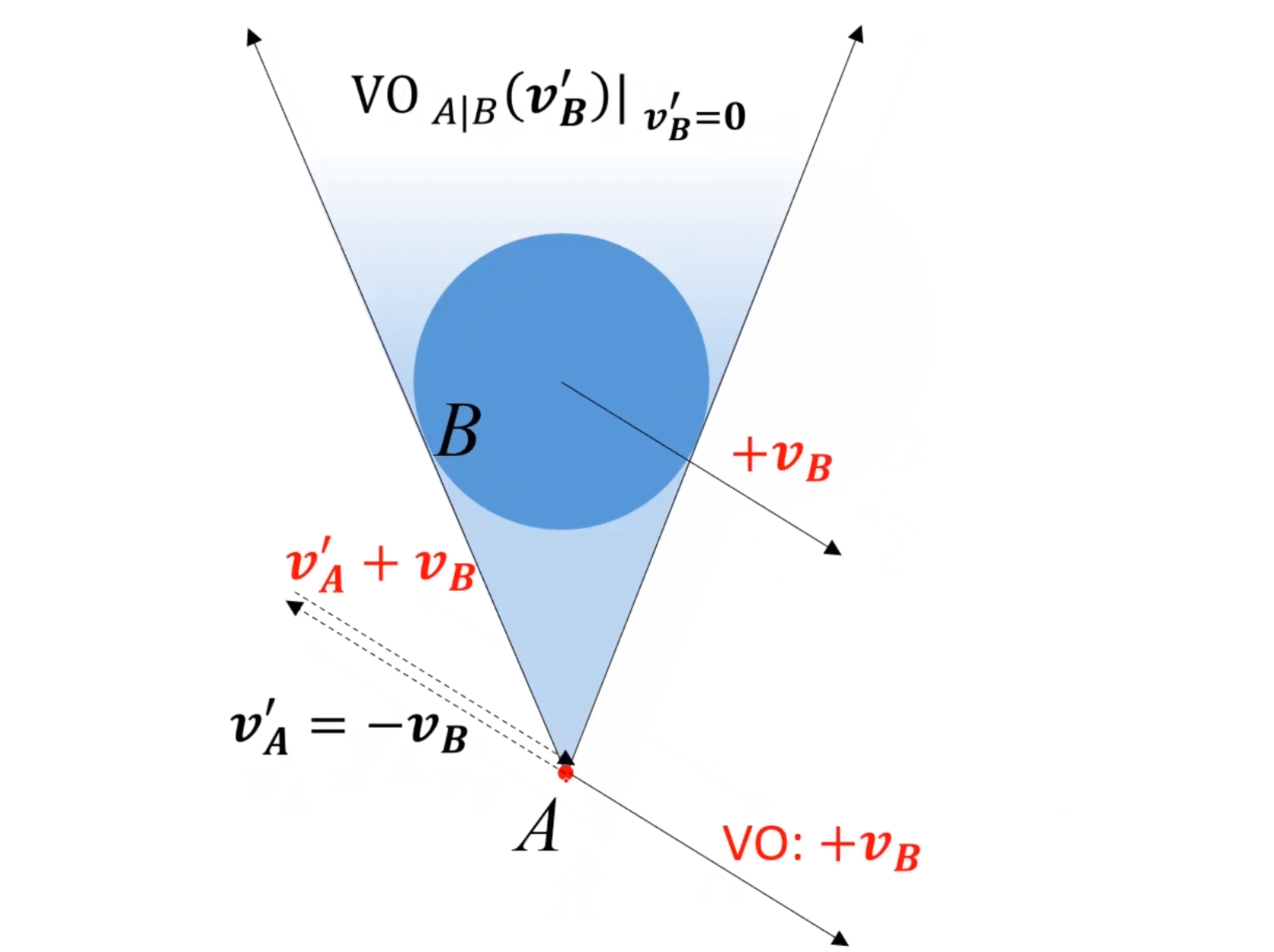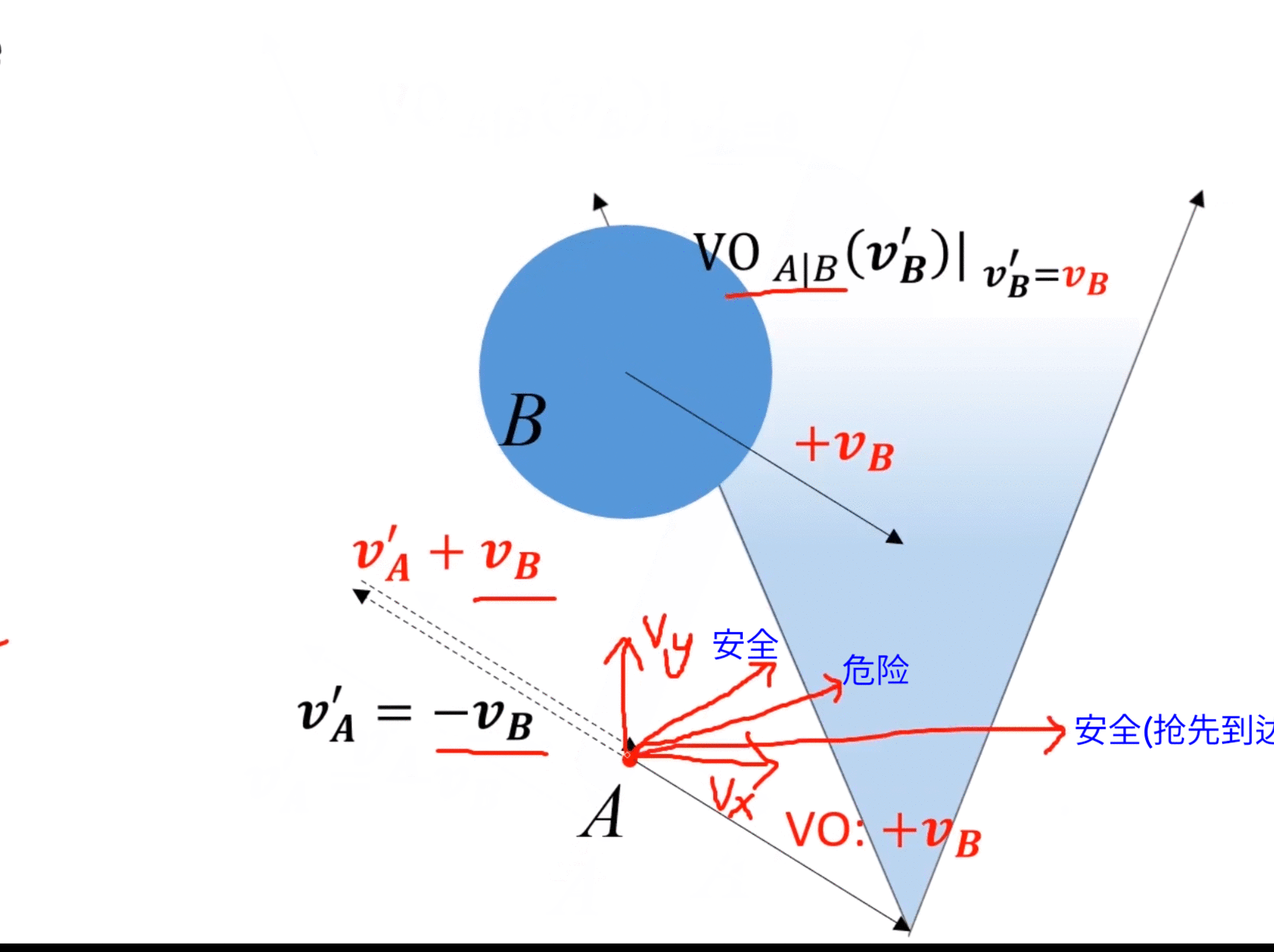
动态情况(障碍物运动):
- 假设障碍物 B B B速度为 v B v_B vB,那么等价于速度系内所有其他对象的速度都是 − v B -v_B −vB。
- 因为速度是相对的,所以在速度系内,对所有对象速度都加 v B v_B vB,所有对象速度不变。
- 但是在速度系内,VO的位置发生改变,变到 v B v_B vB的速度终点。
- 对于新的VO,如果A的速度终点在VO内,则会发生碰撞,否则是安全。
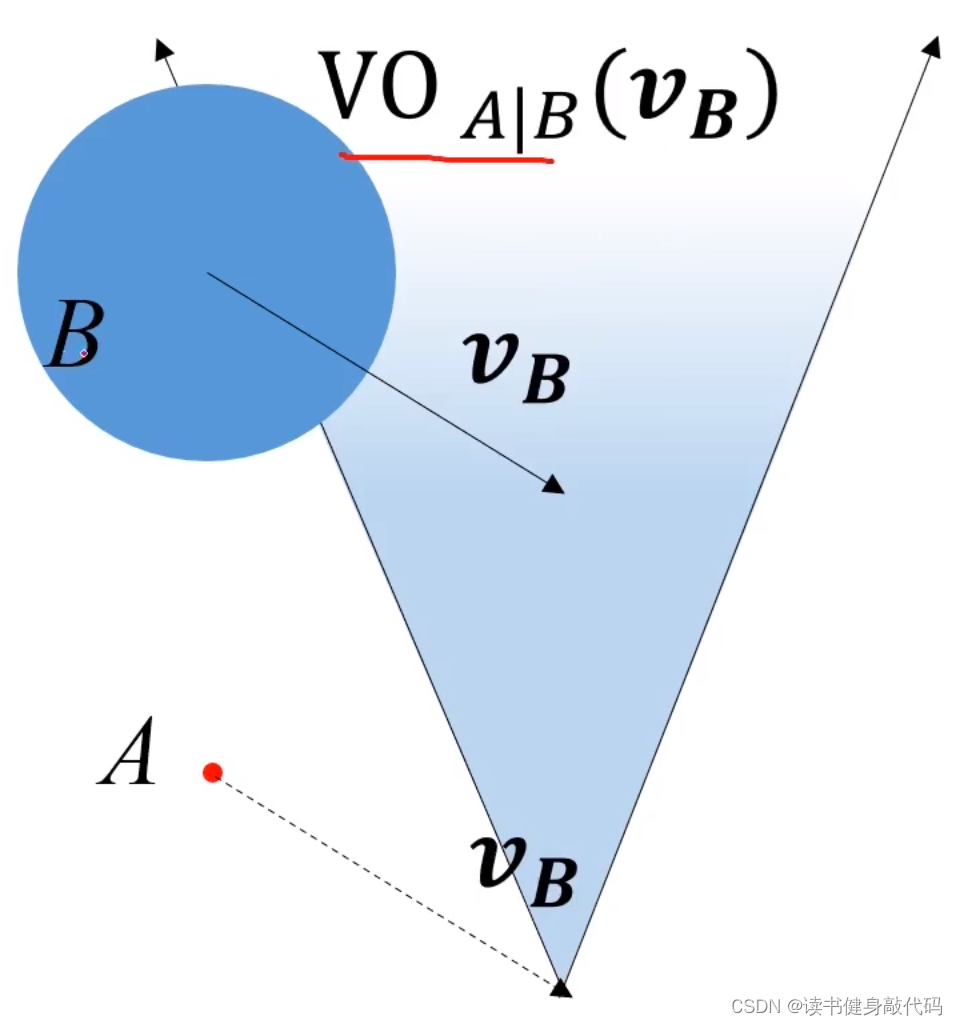
实际情况中可直接将 v B v_B vB平移至A,然后做VO区域 V O A ∣ B ( v B ) VO_{A|B}(\bm{v_B}) VOA∣B(vB),即B相对于A的,与 v B \bm{v_B} vB相关的VO区域。
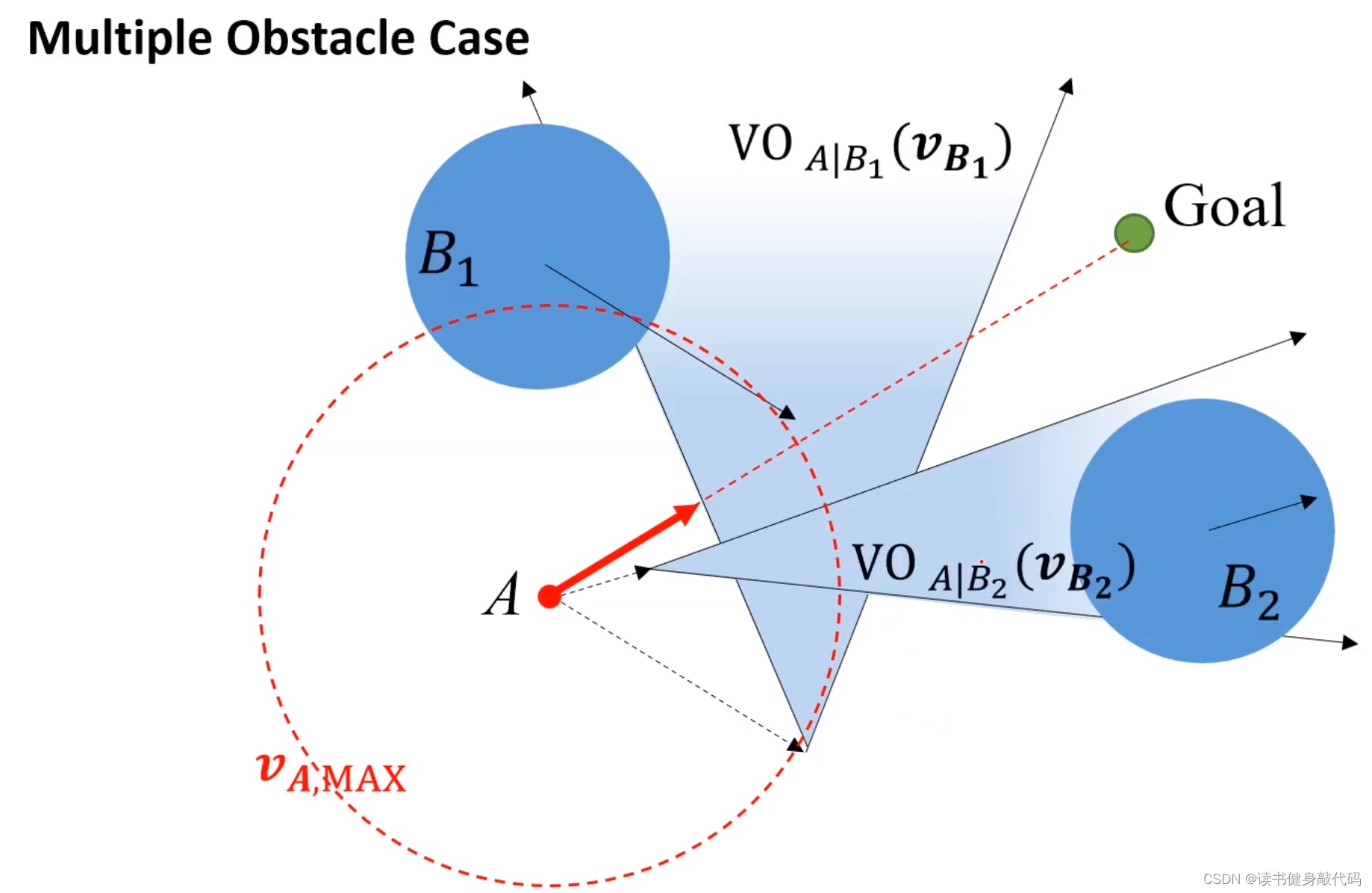
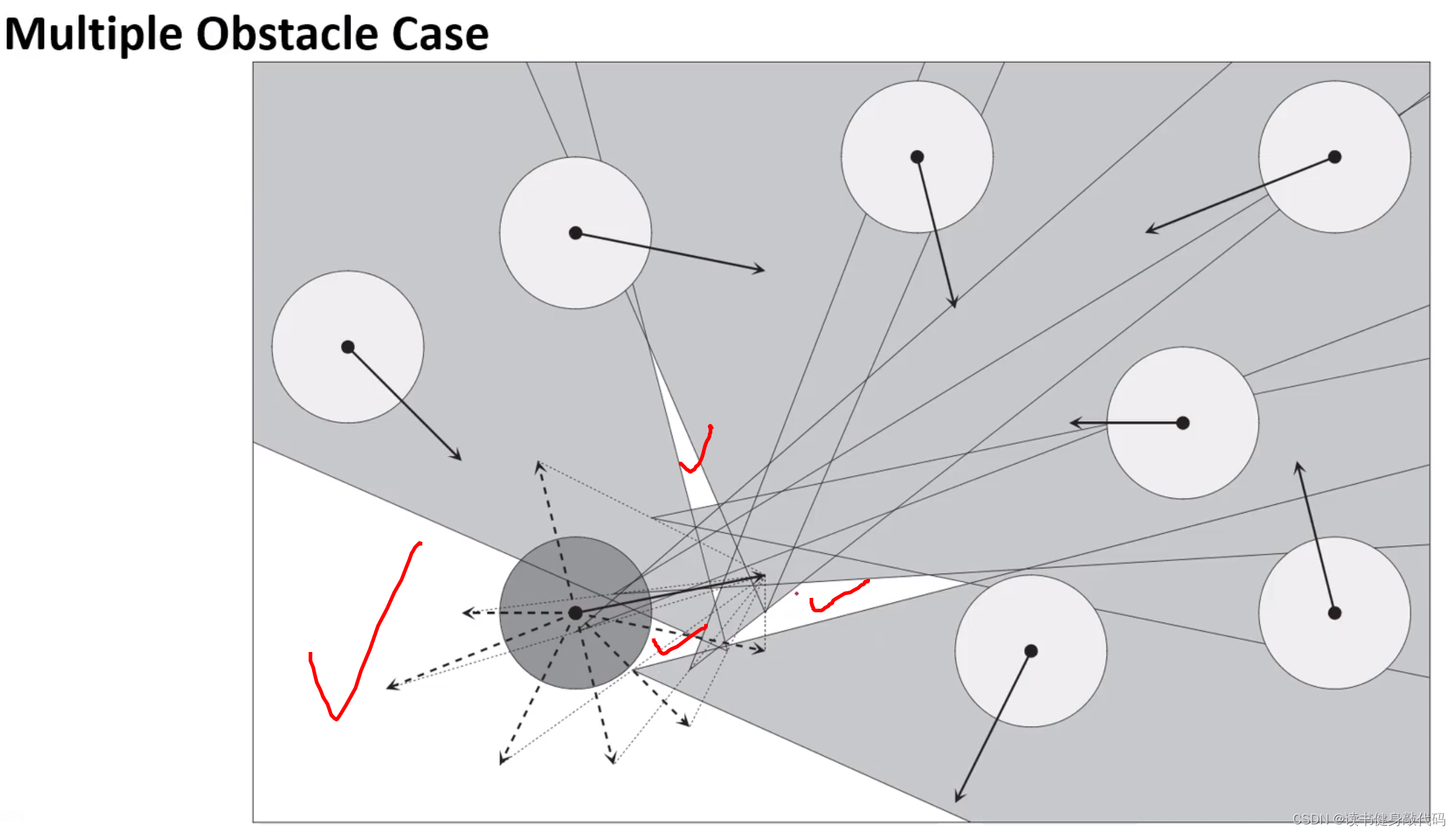
多障碍物情况:
对多个障碍物的速度做平移和各自的VO区域,只要A的速度终点不落在这些VO区域的并集内则为安全,如果考虑上图所示的A的最大速度范围,为了到达Goal,选择红色实线箭头的速度最佳。
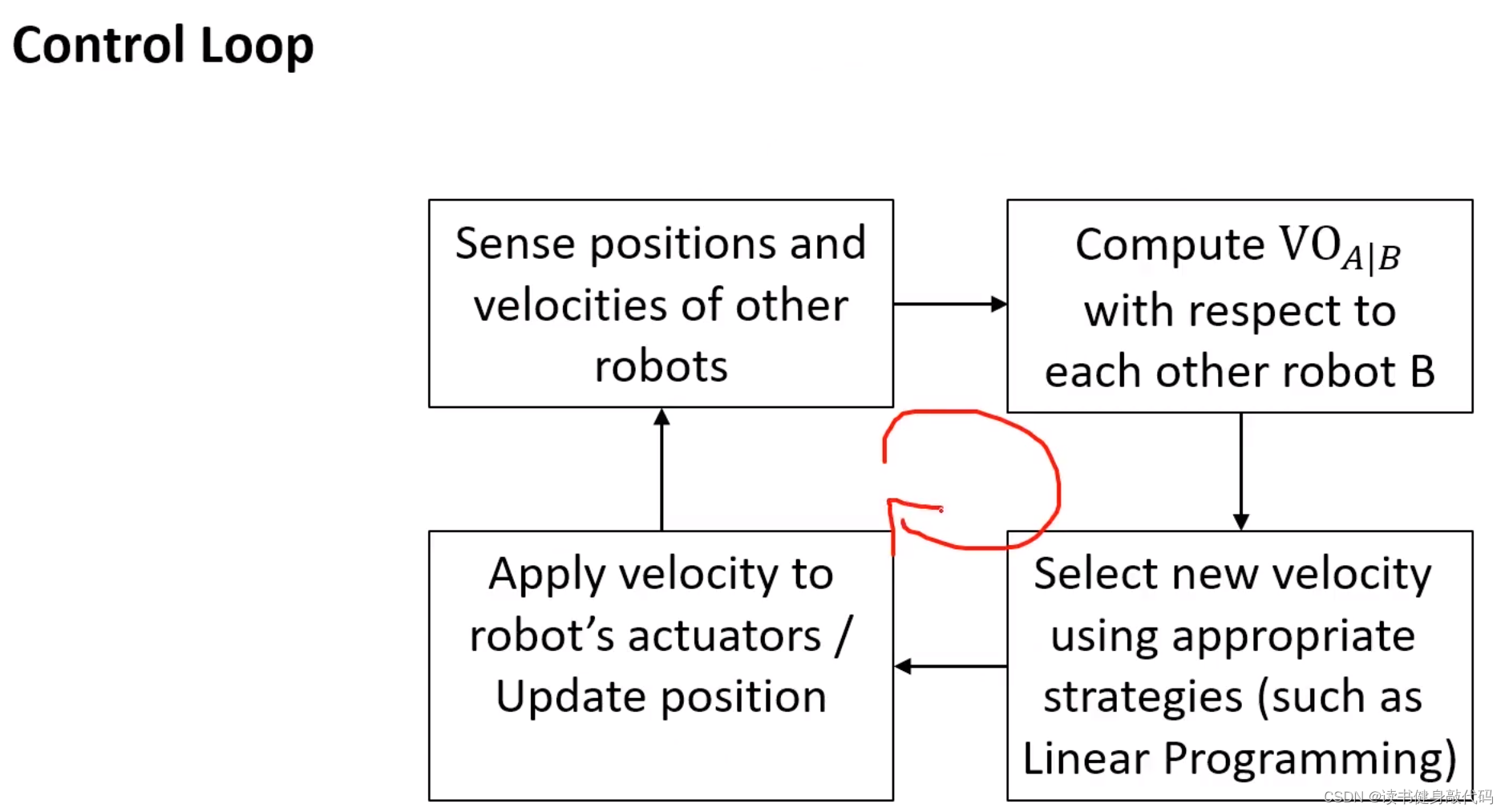
VO实际使用时的控制回路:
- agents广播各自的速度和位置
- 各个VO计算其他agents相对于自己的 V O A ∣ B VO_{A|B} VOA∣B(对于自己来说,其他的agents都是障碍物)
- 使用合适的策略选择速度
- 自己执行该速度,更新状态
2.2. RVO

“Reciprocal” 这个词可以根据不同的语境有多种意思。
- 在数学和工程学中,它通常指的是倒数,即一个数与它的乘积等于1的另一个数。
- 在人际交往或社会科学中,“reciprocal” 描述的是互相交换的、相互的行为或关系,比如说,“reciprocal agreement”(相互协议)指的是两方都有给予和接受的协议。
在“Reciprocal Avoidance”这个词组可以翻译为“相互避让”或“互避”。“reciprocal” 通常指的是双向的或者相互的行动,意味着每个个体都在考虑对方的动作来调整自己的行为,以此实现共同的目标,比如避免碰撞。
VO会存在轨迹zigzag的现象,因为轨迹在下个不考虑其他agents的速度,为了解决这个问题,提出了RVO
(ref[8])
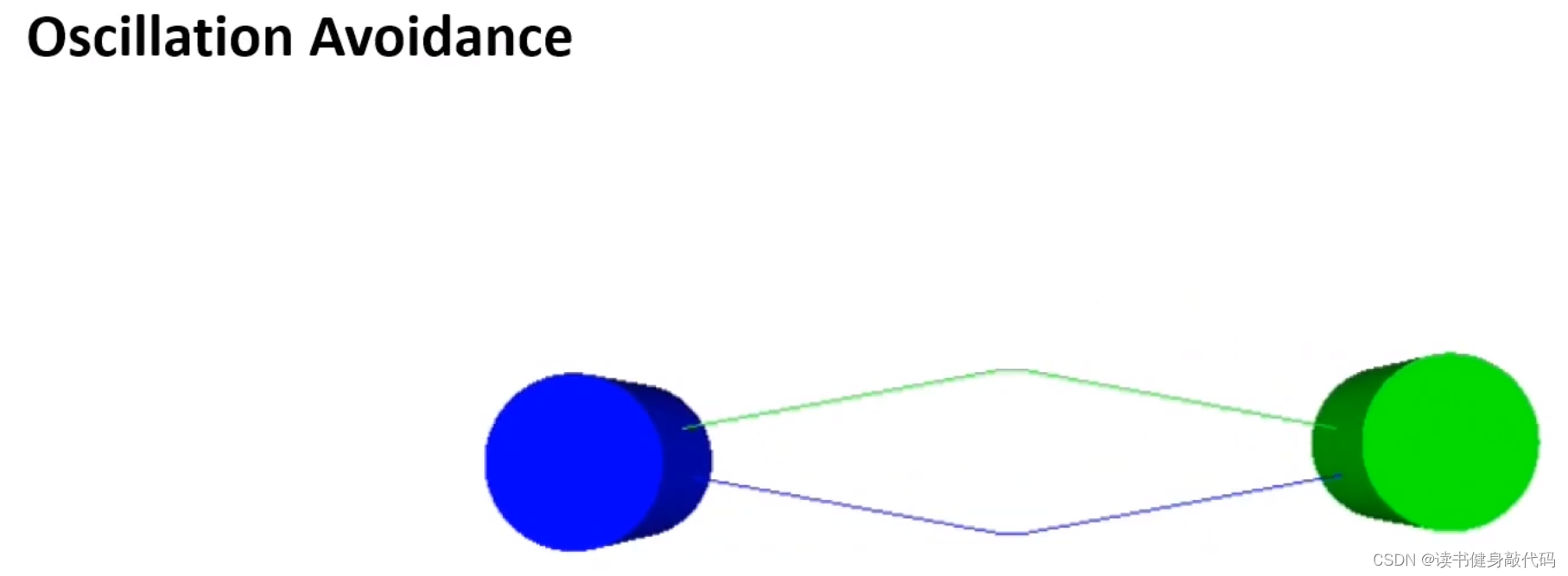
RVO比VO顺滑很多。
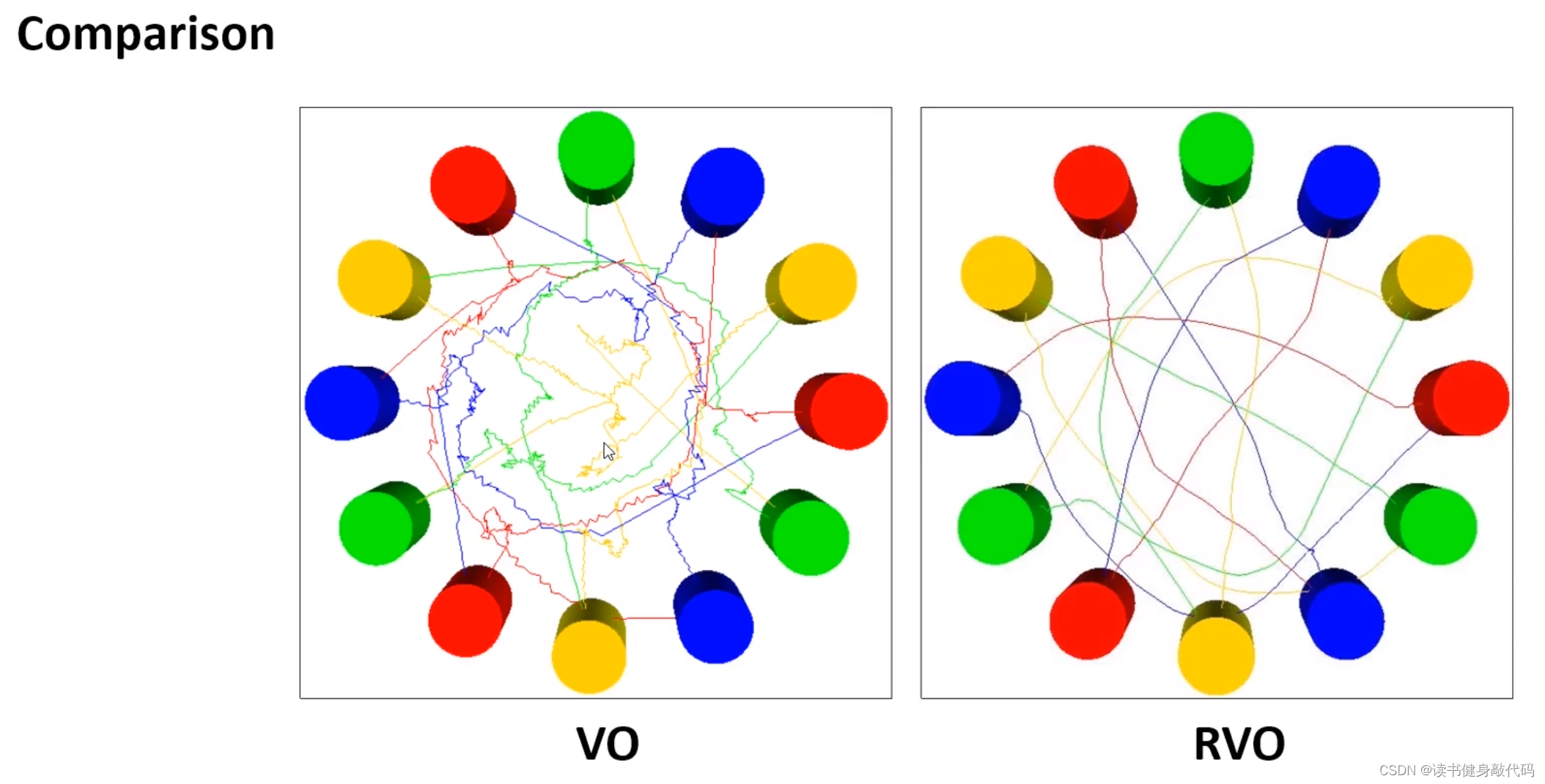
更加直观的例子。

main idea:两个agents都运动,都相互避让,本来避让一个身位即可完成避障,但是由于对方也在避障,所以总共避障了2个身位,相对了调整2个身位,调整较大,造成了zigzag。如果每个agents只调整半个身位(或者不严格一半,但二者加起来为一个身位),则也可完成避障,于是就有了下图所示的“共同承担避障责任”的RVO。
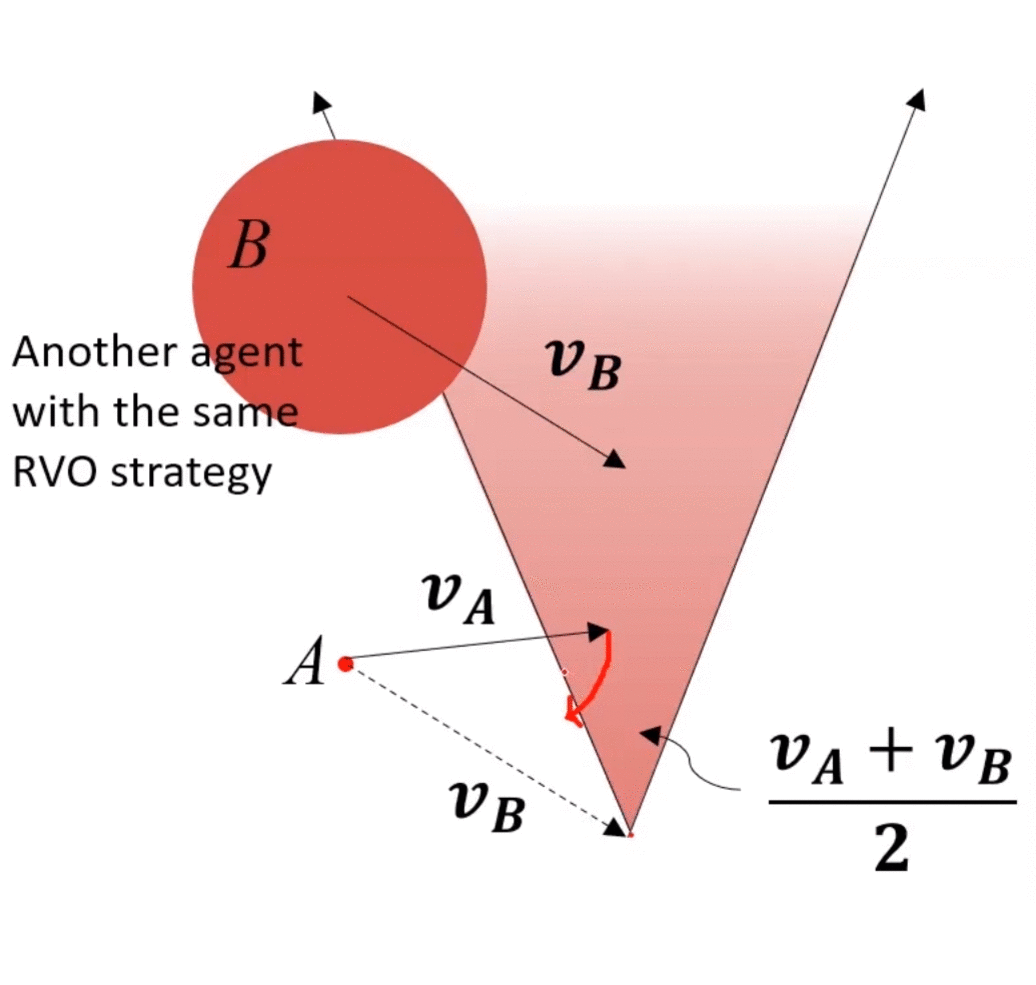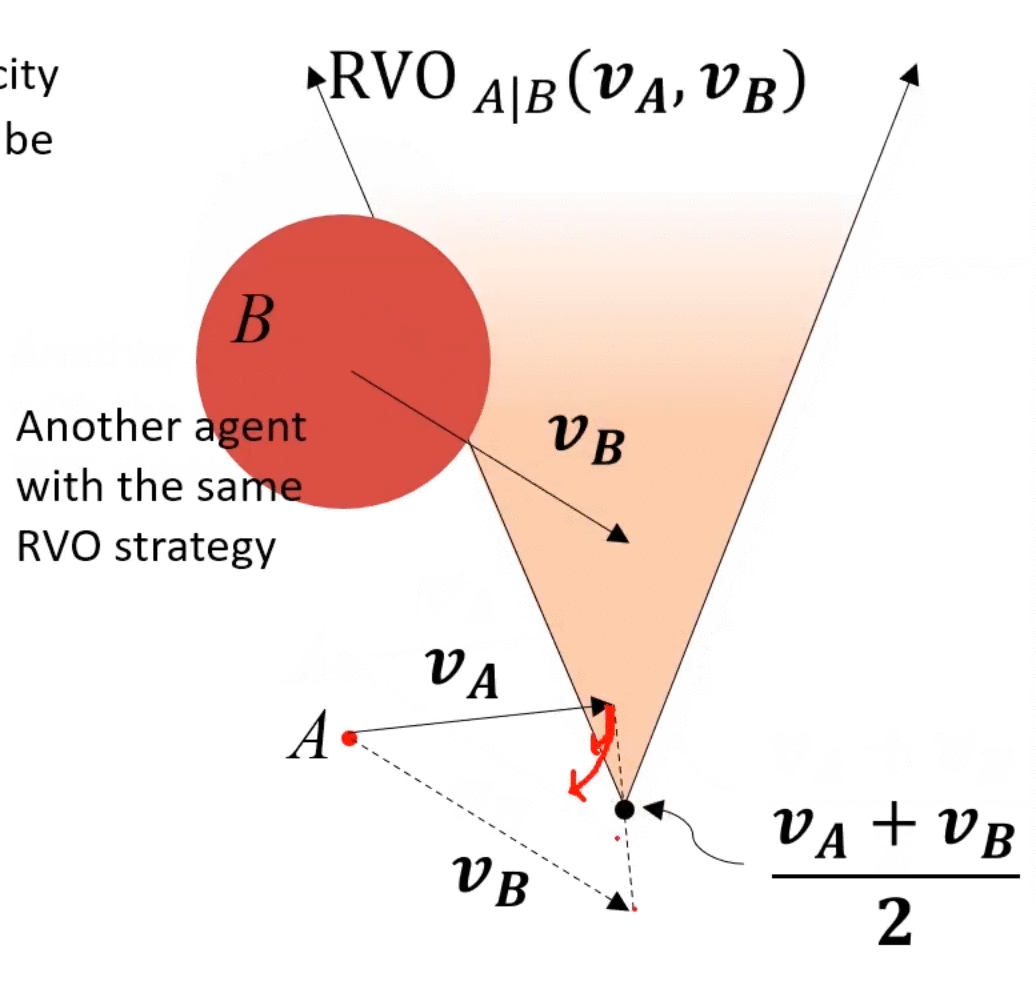
如上图,A的VO上移前,为了保证安全,A需要调整一个较大角度才能避免碰撞,而将A的VO上移之后,A仅需调整一个较小角度即可保证安全。
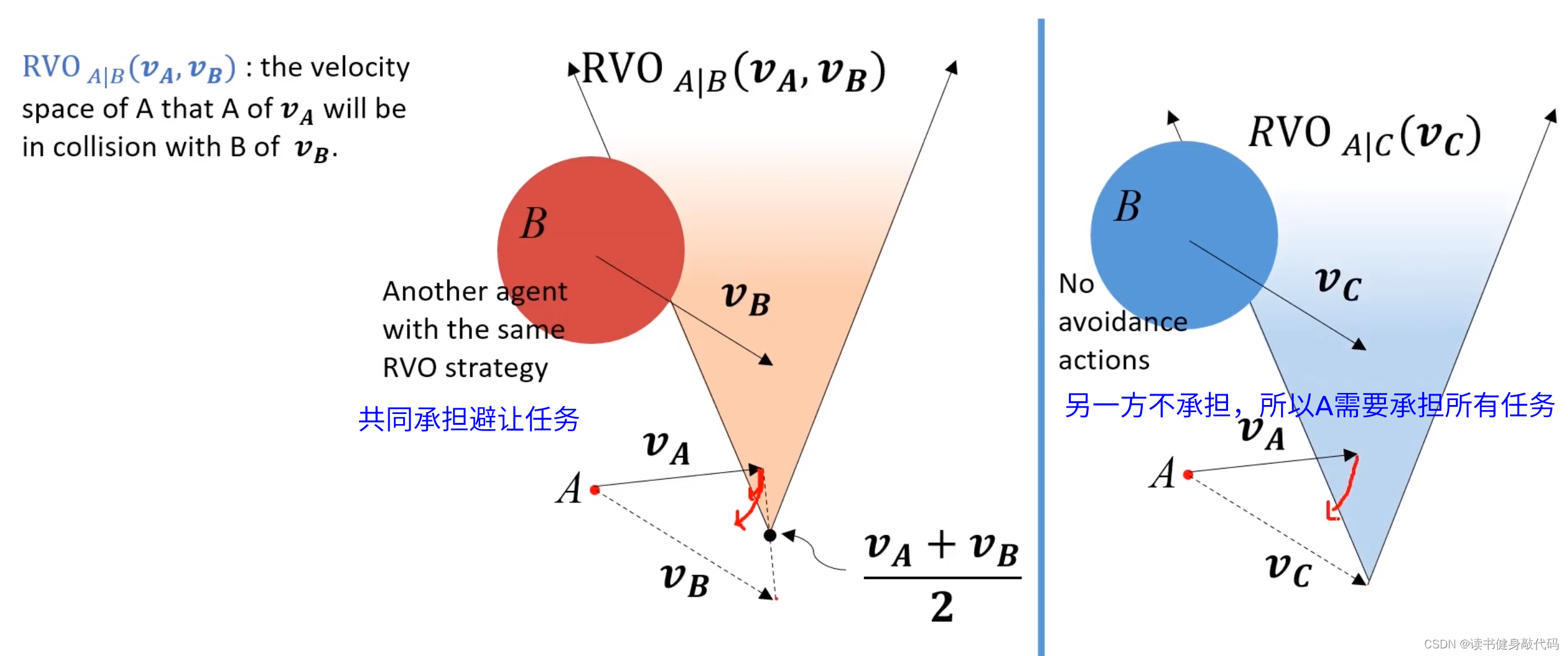
另一方不承担任务时,对于该agent,还与VO一样承担所有任务。
若双方均承担避让任务,可减小zigzag的情况。
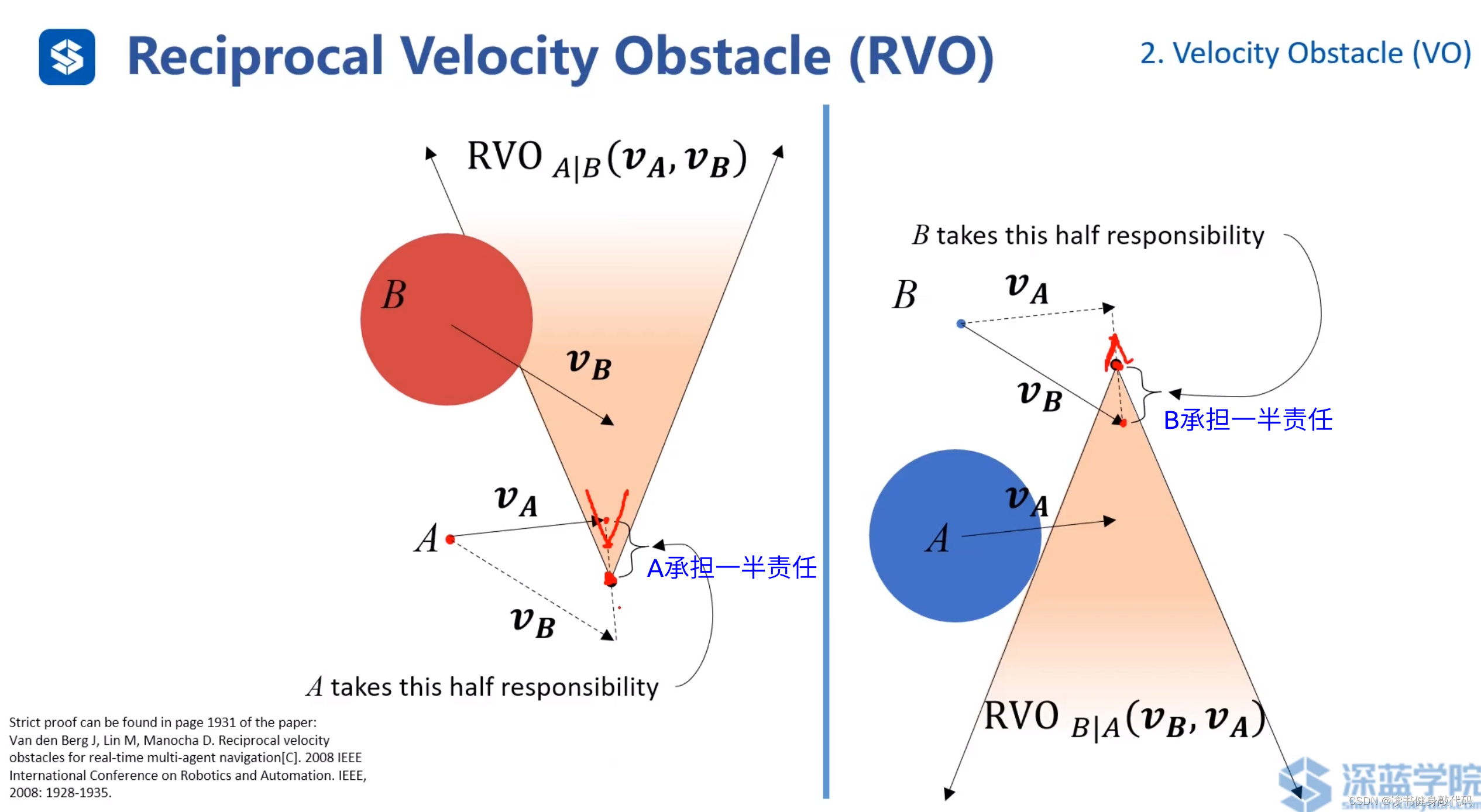
上图为了说明速度,对原问题的位置进行了旋转。
如上图,在白色区域内选择速度则不会与任何agents发生碰撞。
2.3 ORCA
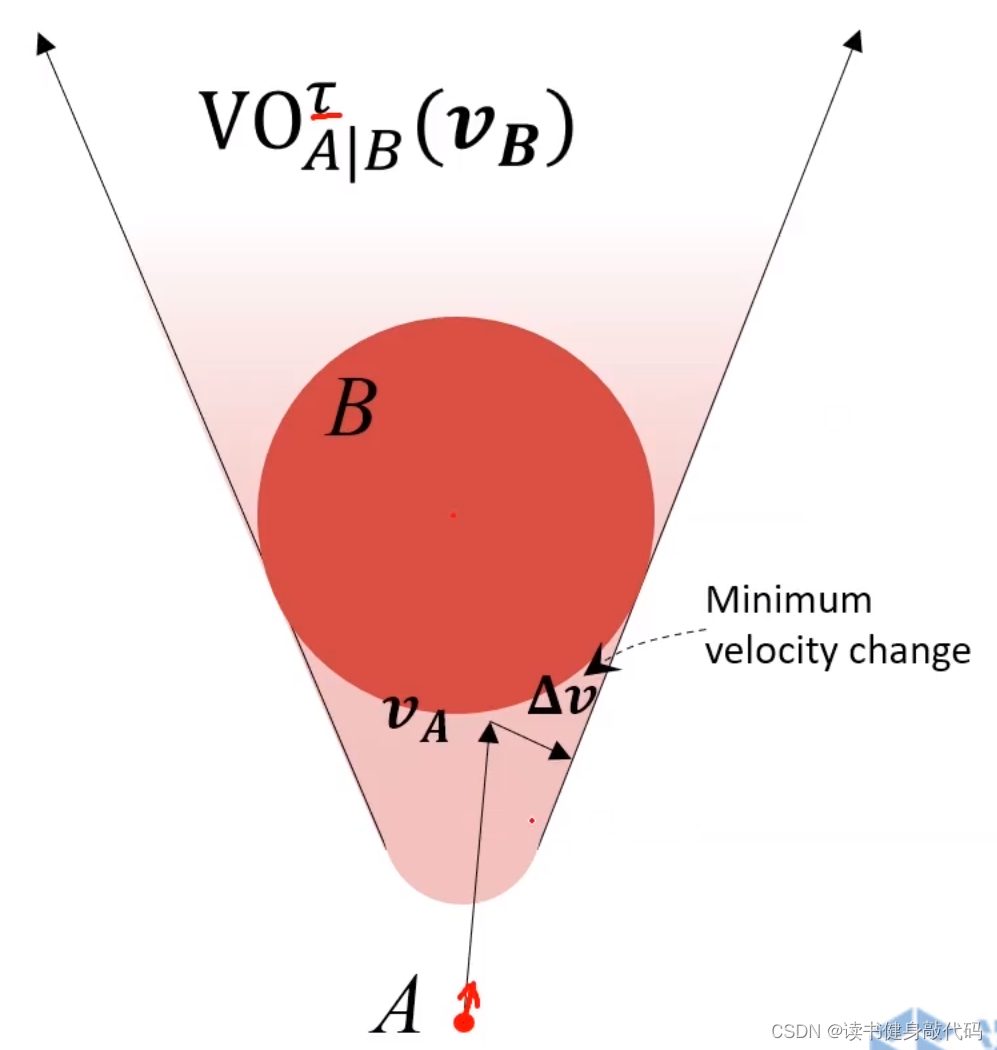
考虑上述情况,A为了避免碰撞,需要对速度 v A \bm{v_A} vA进行 Δ v \bm{\Delta v} Δv的改变才能保证安全,那么取 Δ v \bm{\Delta v} Δv的中垂线,取靠近free space侧的半平面,记作 O R C A A ∣ B τ ORCA^{\tau}_{A|B} ORCAA∣Bτ,如下图所示,其中 τ \tau τ是避障有效时间,只关心在 τ \tau τ时间内不会碰撞,所以VO是圆头的,具体细节此处不深究,可参考ref[9](Optimality definition and proof can be found in pages 6-9 of the paper)。

上图即为ORCA半平面
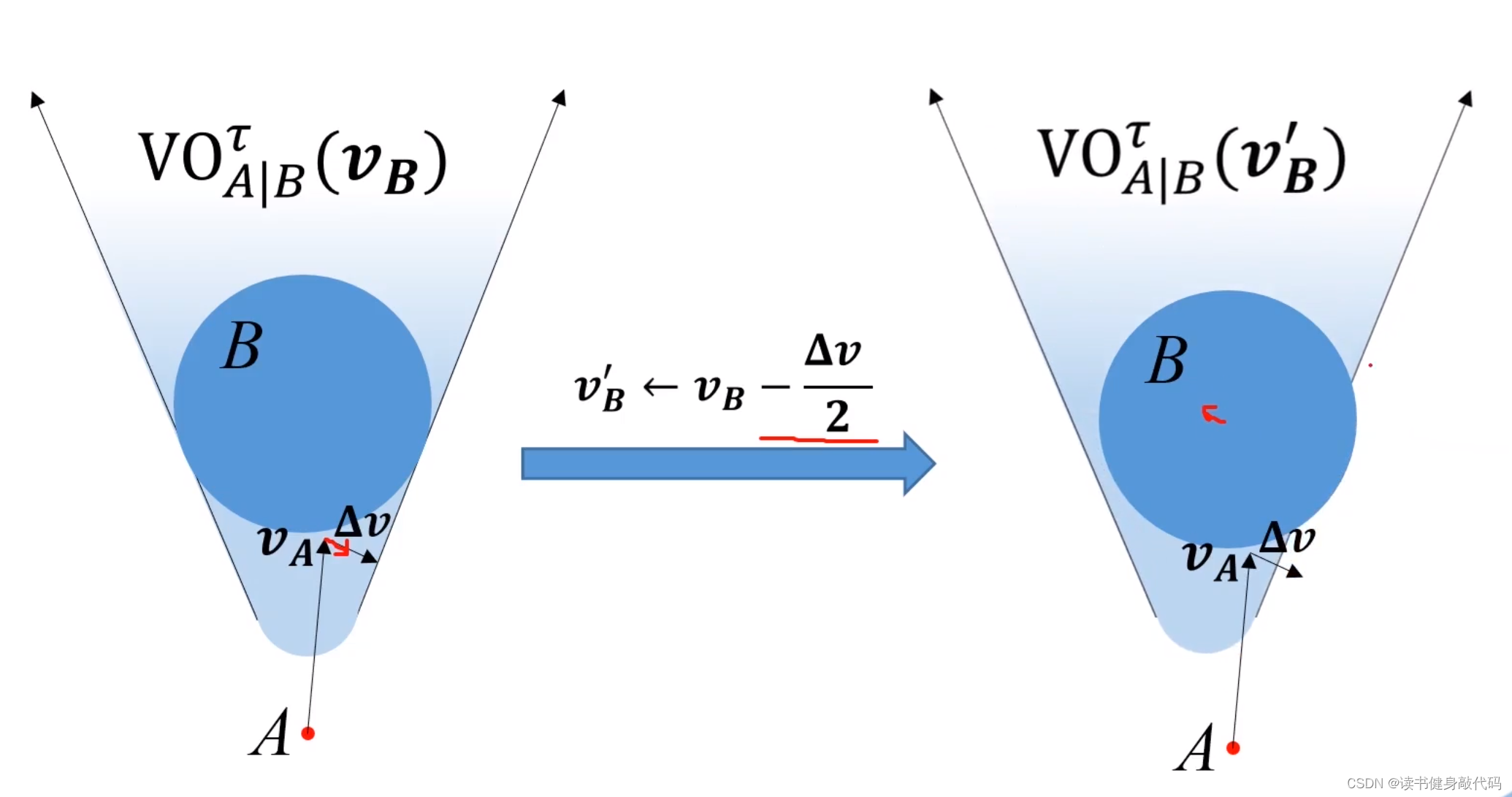
上图中,总该变量为 Δ v \bm{\Delta v} Δv,A往右下改变 1 2 Δ v \frac{1}{2}\bm{\Delta v} 21Δv,B往左上改变 1 2 Δ v \frac{1}{2}\bm{\Delta v} 21Δv,动图如下所示:
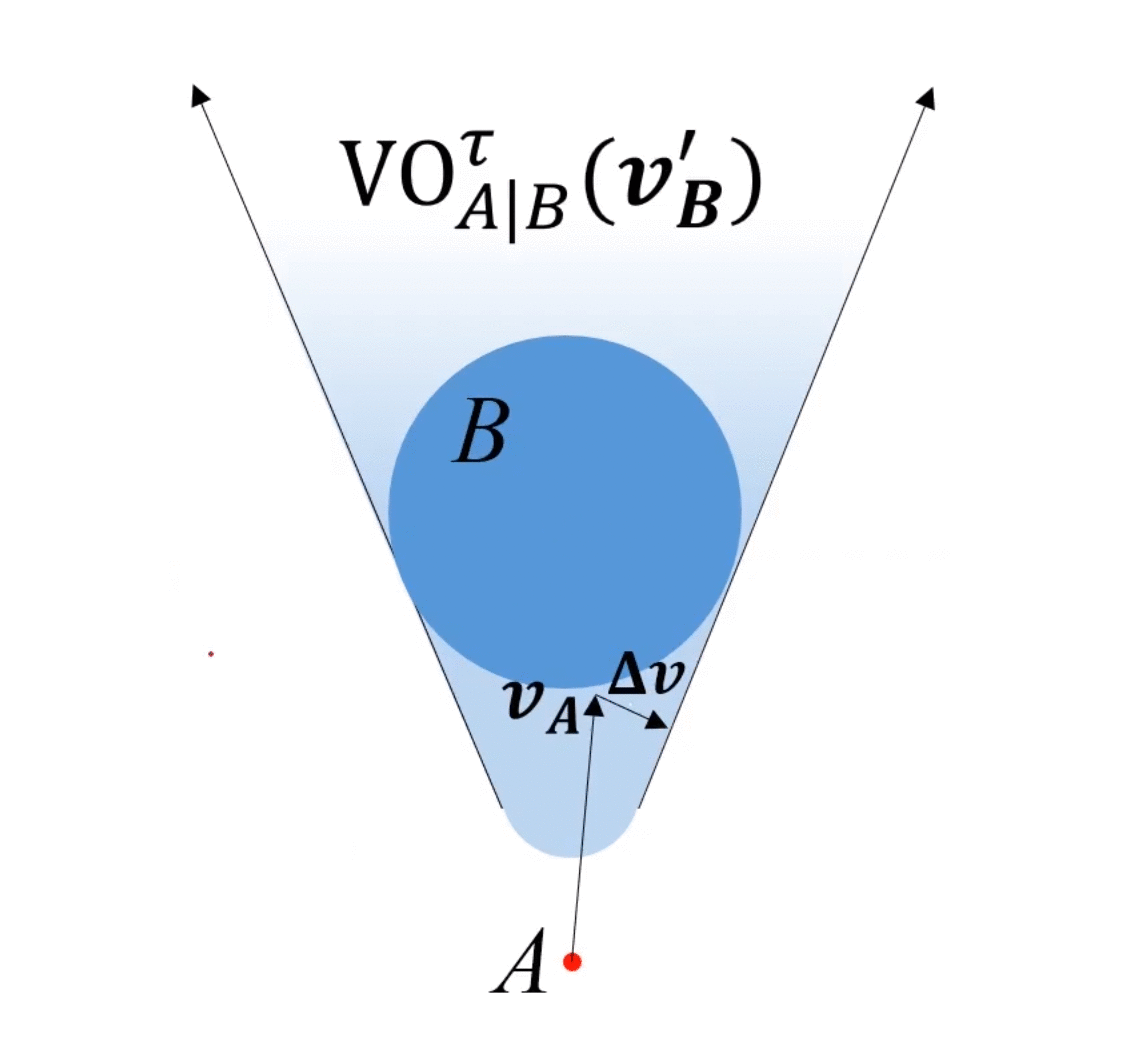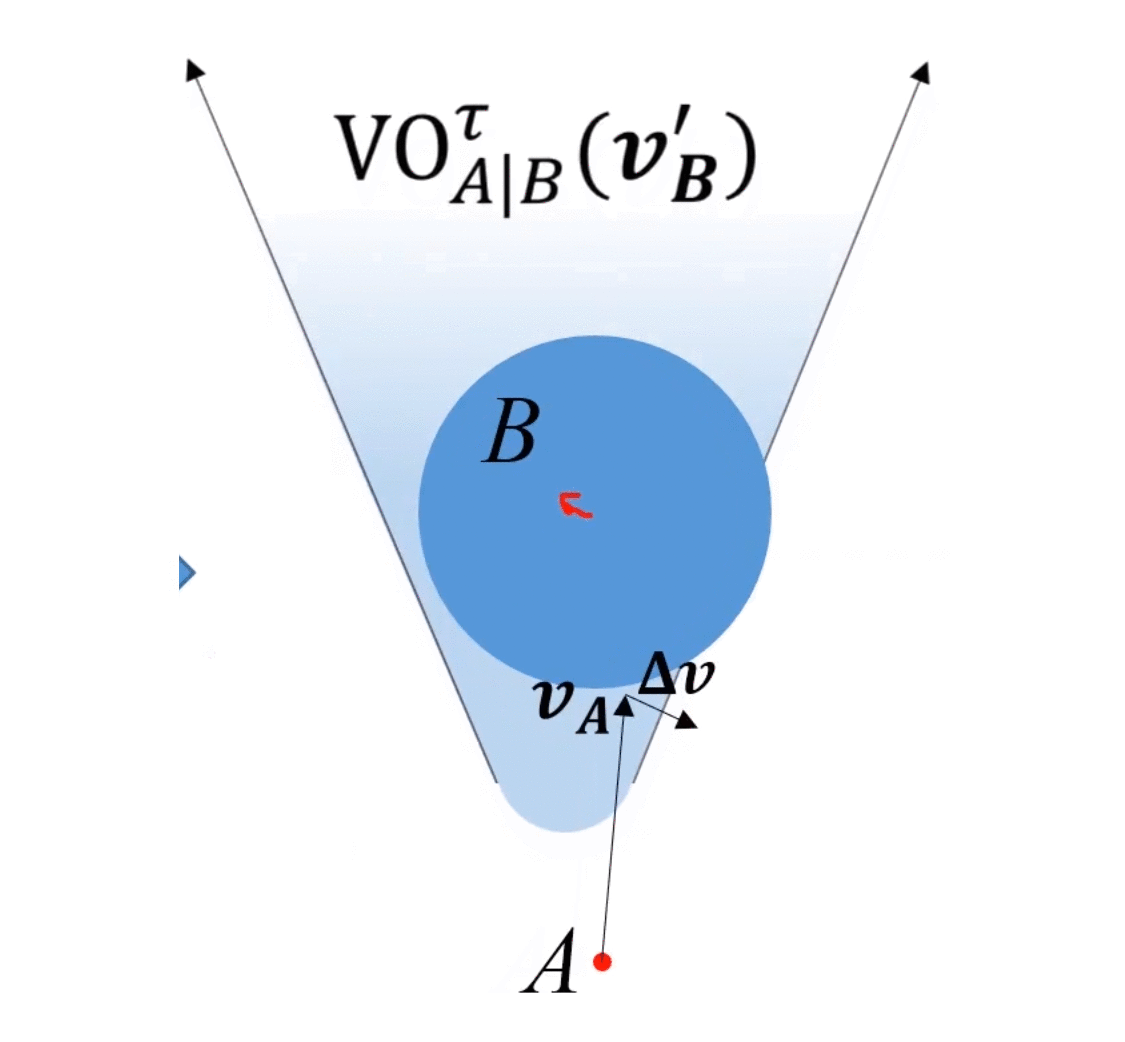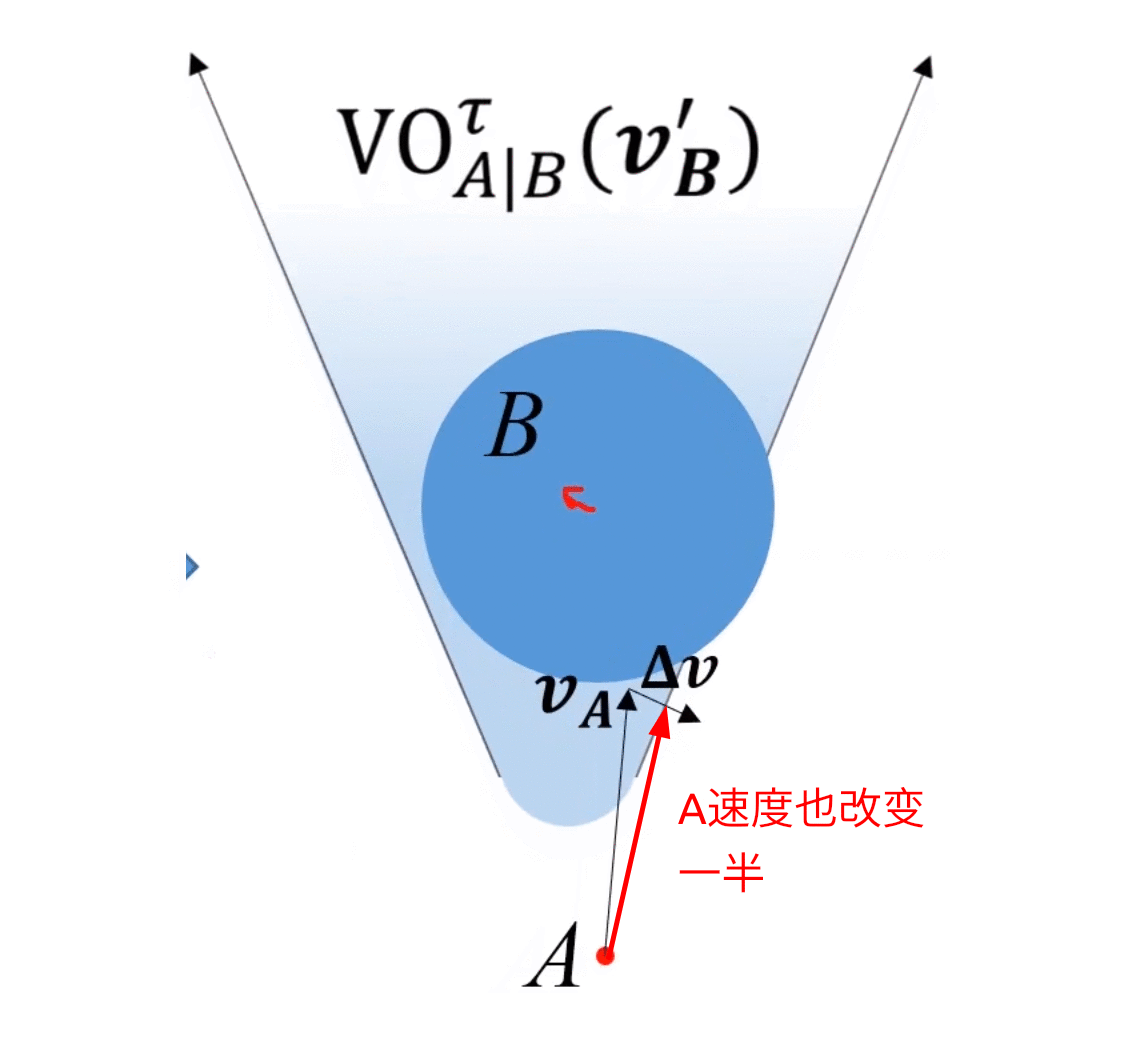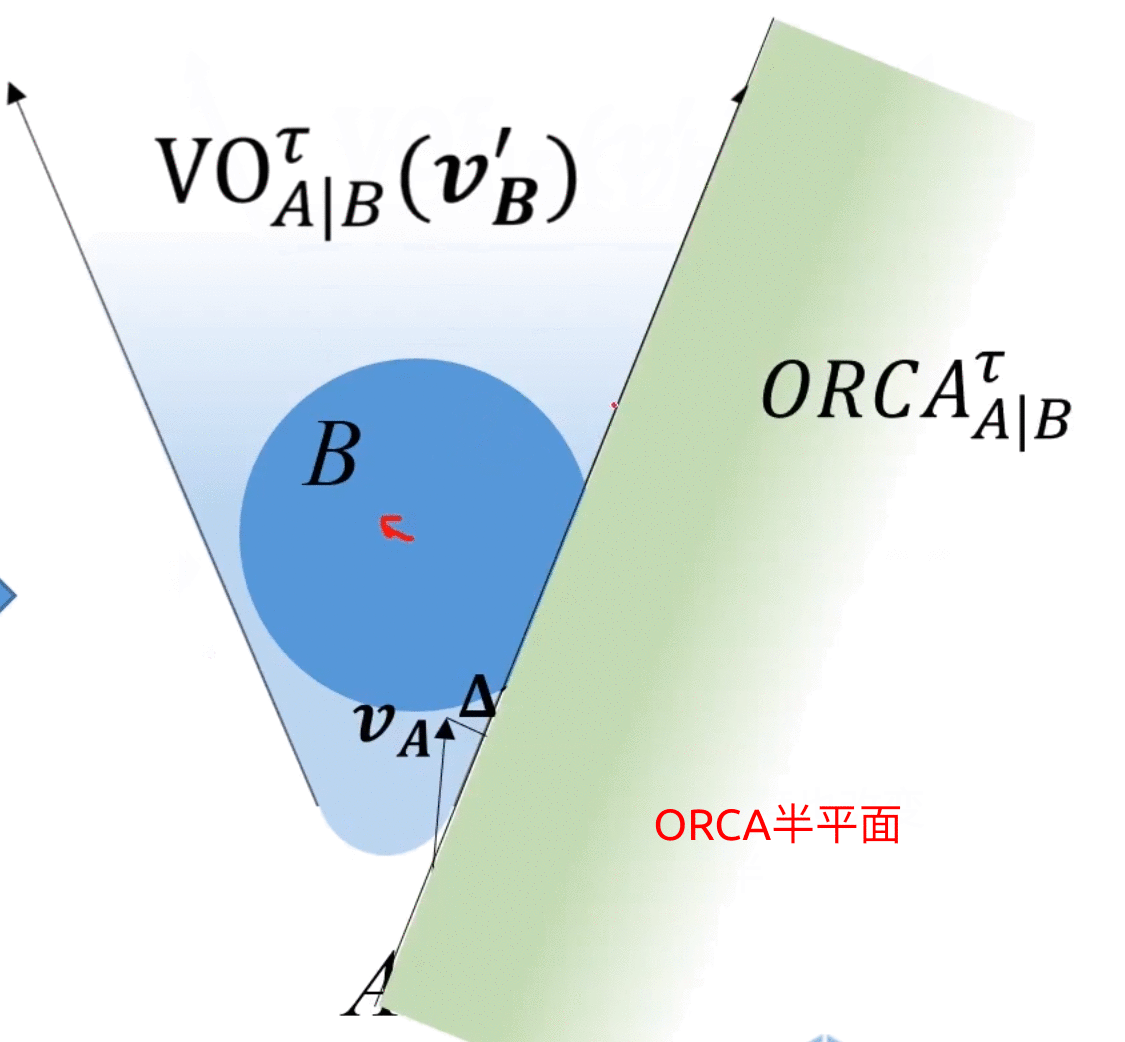
ORCA的精髓:二者以最小速度该变量为基准,分别承担 1 2 \frac{1}{2} 21的改变量。
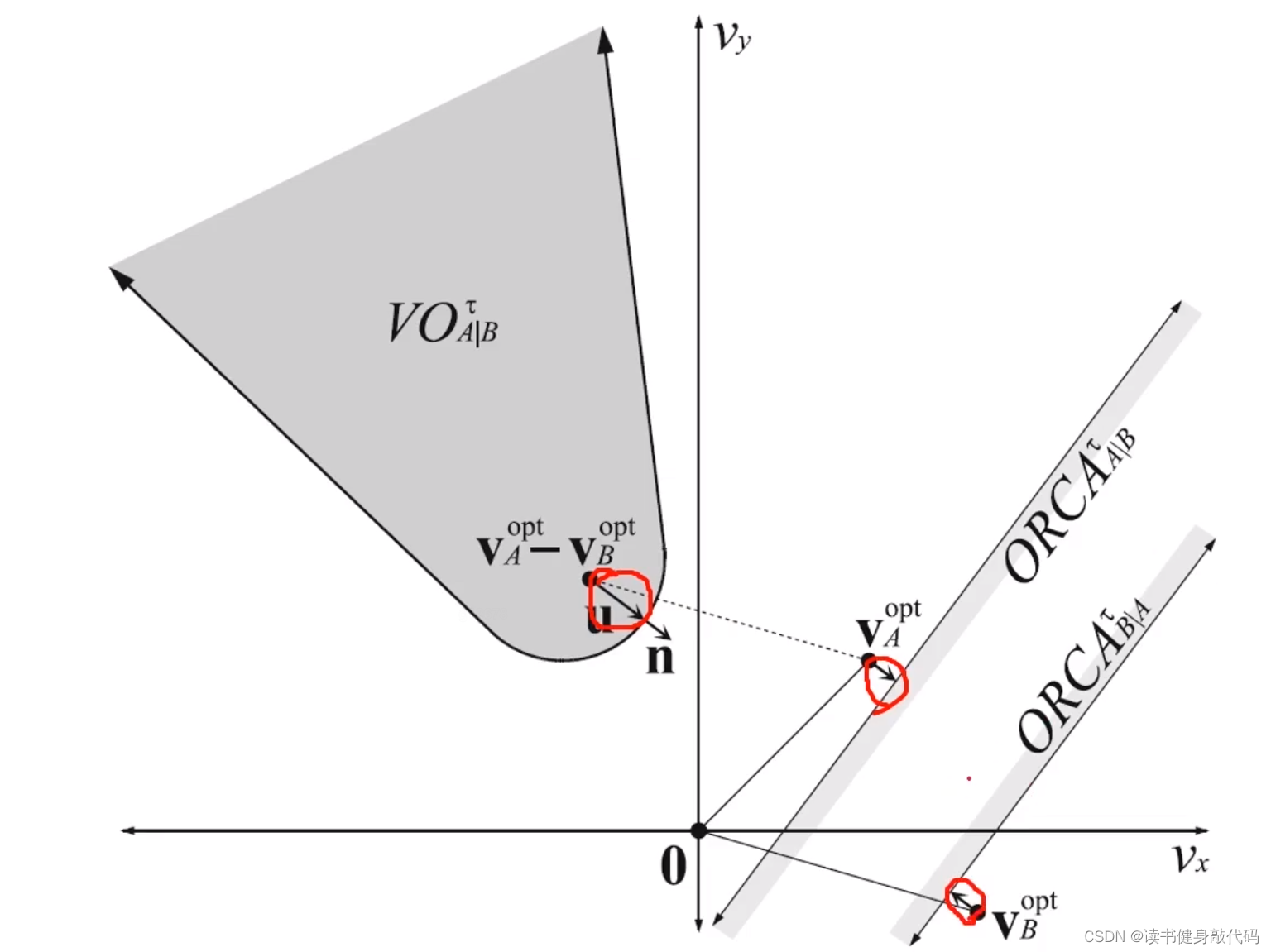
论文中例子, O R C A A ∣ B τ ORCA^{\tau}_{A|B} ORCAA∣Bτ和 O R C A B ∣ A τ ORCA^{\tau}_{B|A} ORCAB∣Aτ的阴影部分是做出改变的部分(按照我的理解)
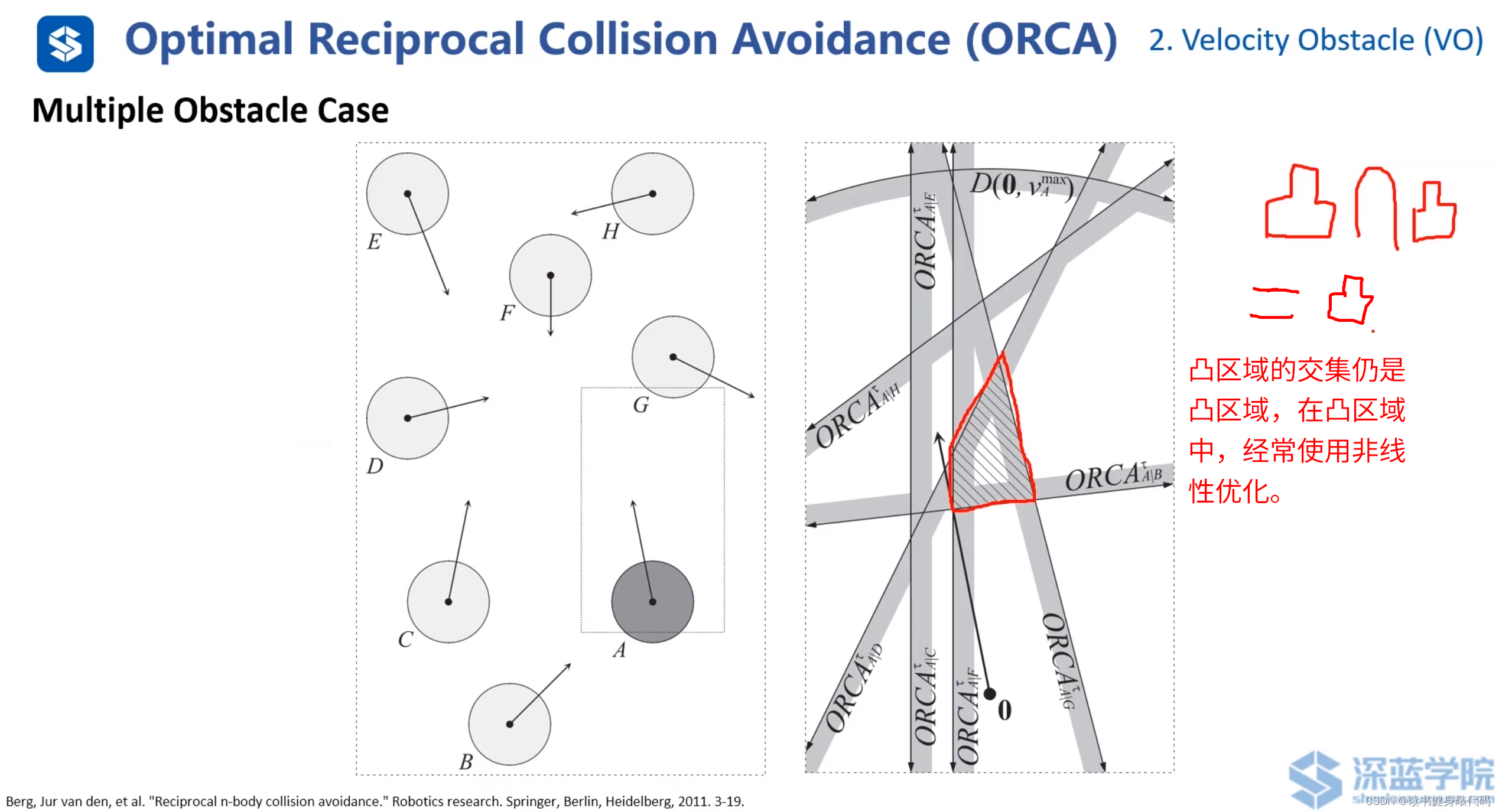
多障碍物避障,取ORCA的交集围成的区域,半平面为凸区域,其交集仍为凸区域。
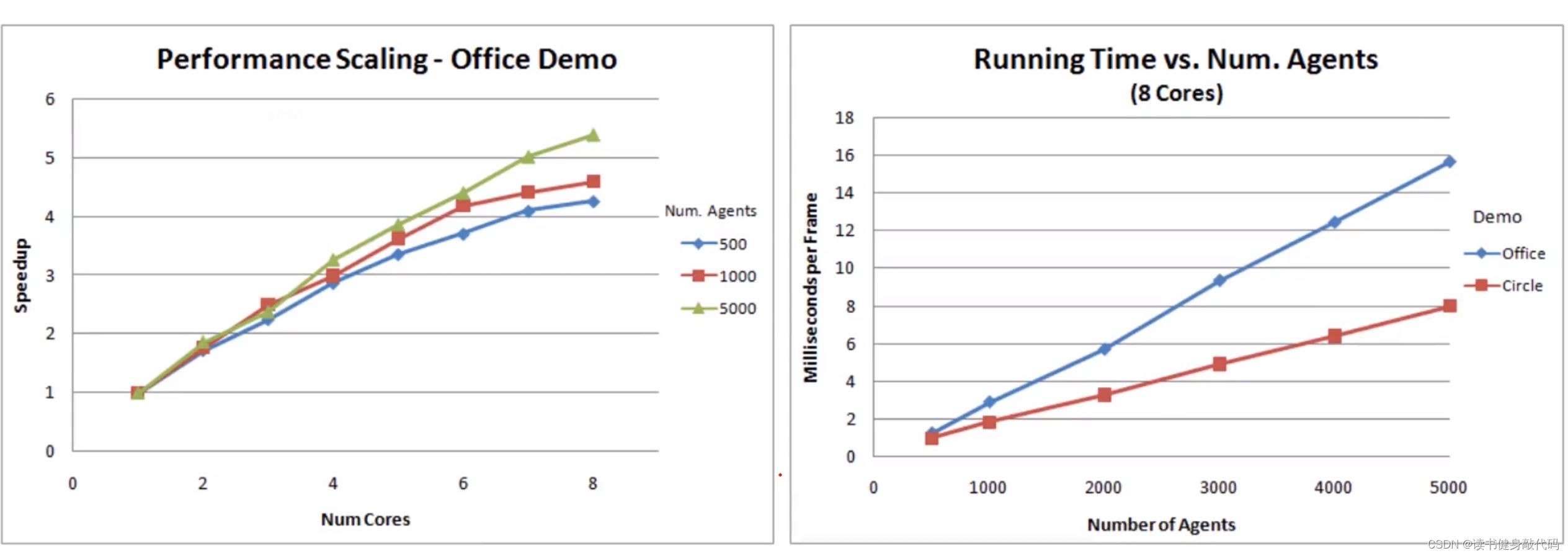
尤其在agents数量多时,ORCA的复杂度和计算消耗较低。
3. Flocking model(群落模型)

ref[10],主要是参考鸟类等种群开发的算法。

main idea:每个agent有短期,中期和长期的速度。
短期: 防止与障碍物和周围其他agent碰撞。(凸如上图的曲线,当距离另外的agent较远的时候,此项为0,较近的时候有速度)
中期:和周围的agents保持大致相同的速度。
长期:整体朝着目标前进。
三个速度(或推力)加权求和,算出总速度(推力)。
优点:模拟自然界的动物群落。
缺点:参数很多,对调参要求高。
解决方法:一些自动调参的策略等。
4. Trajectory Planning for Swarms(集群轨迹规划)
本章主要讲解集群机器人轨迹规划的相关原理和应用(应该和Ch5讲的trajectory generation对应)
4.1 Background
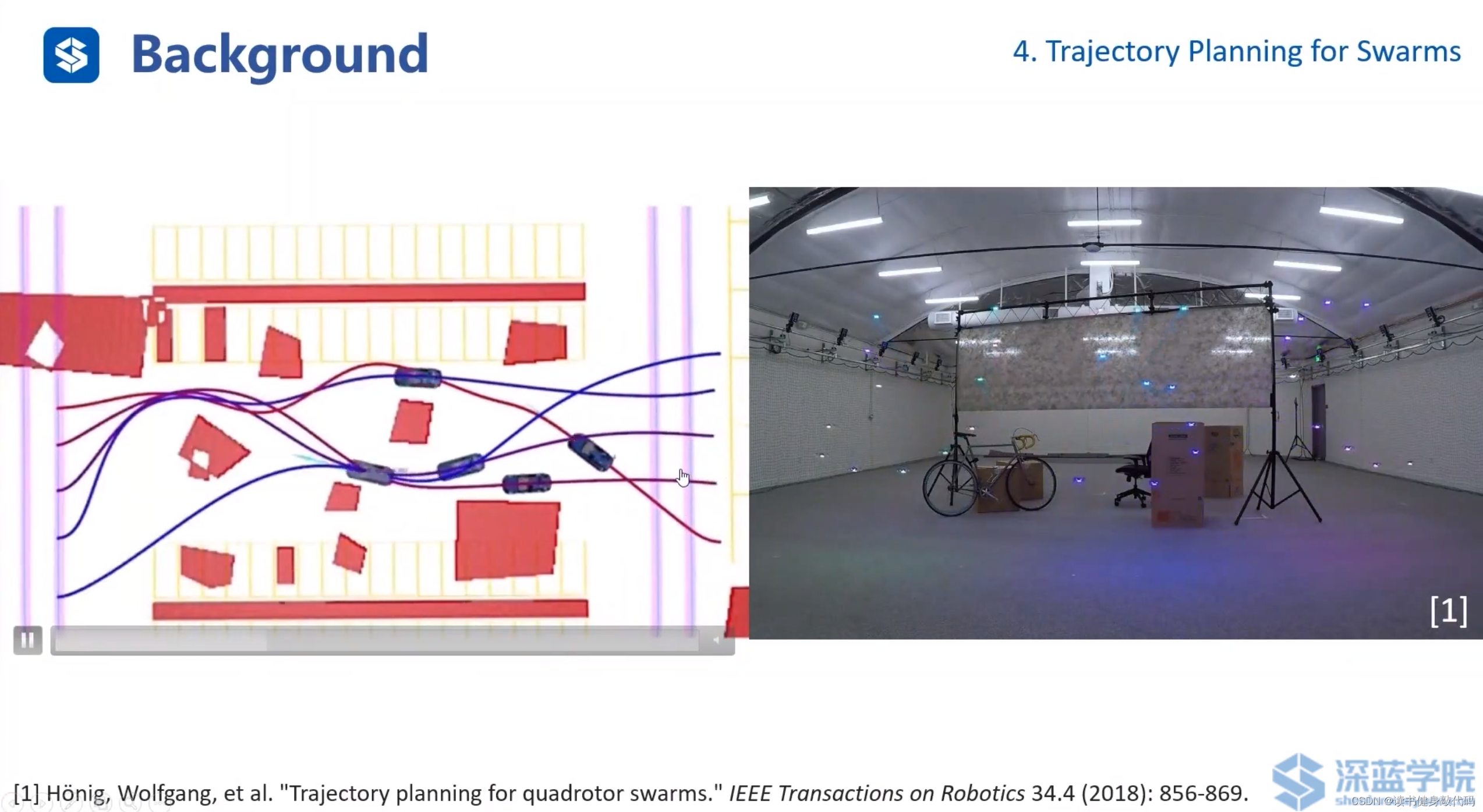
考虑车辆/无人机动力学模型的,多辆车辆的traj生成。ref[11]
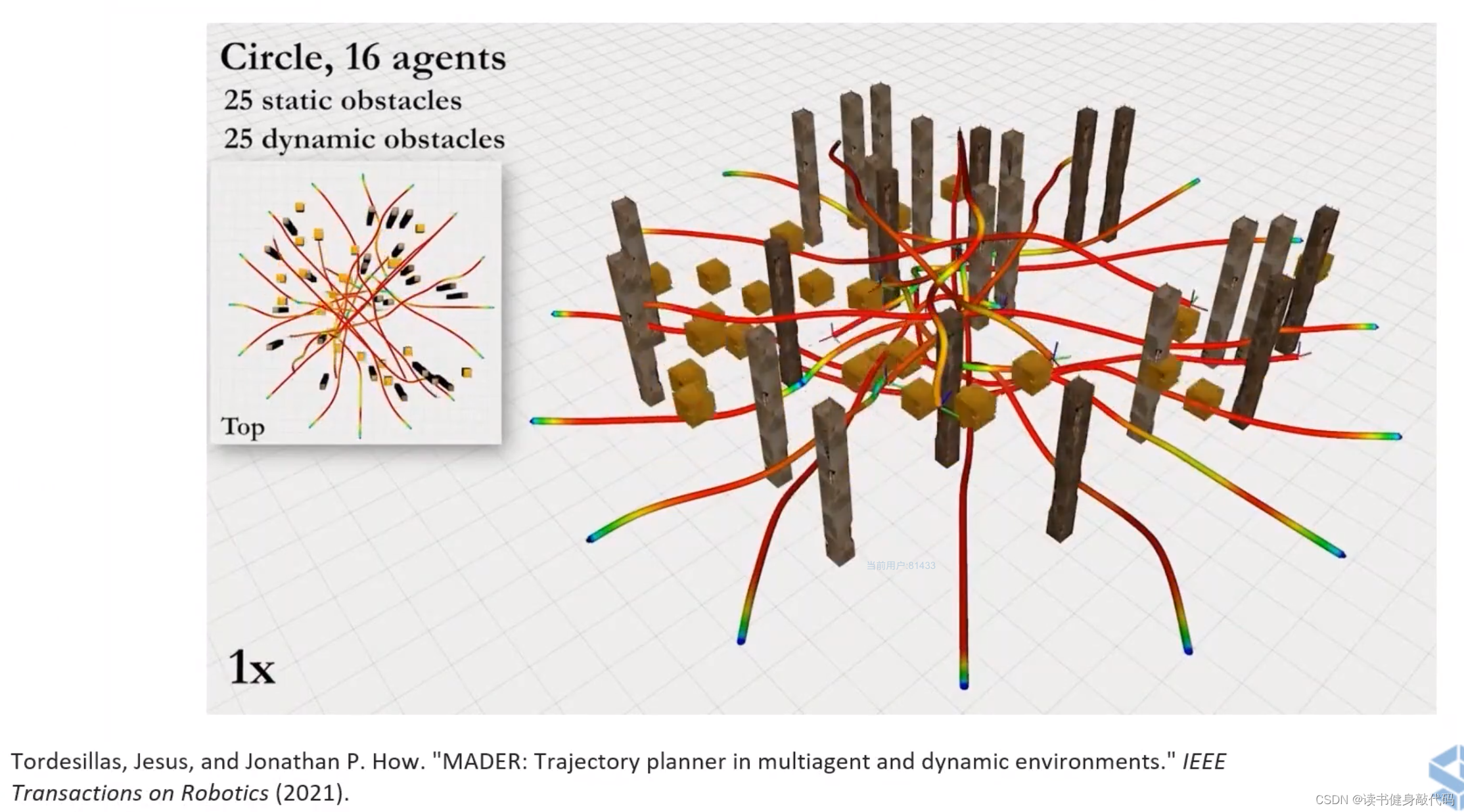
有静态和动态障碍物的轨迹规划控制。

ZJU FAST LAB的工作。
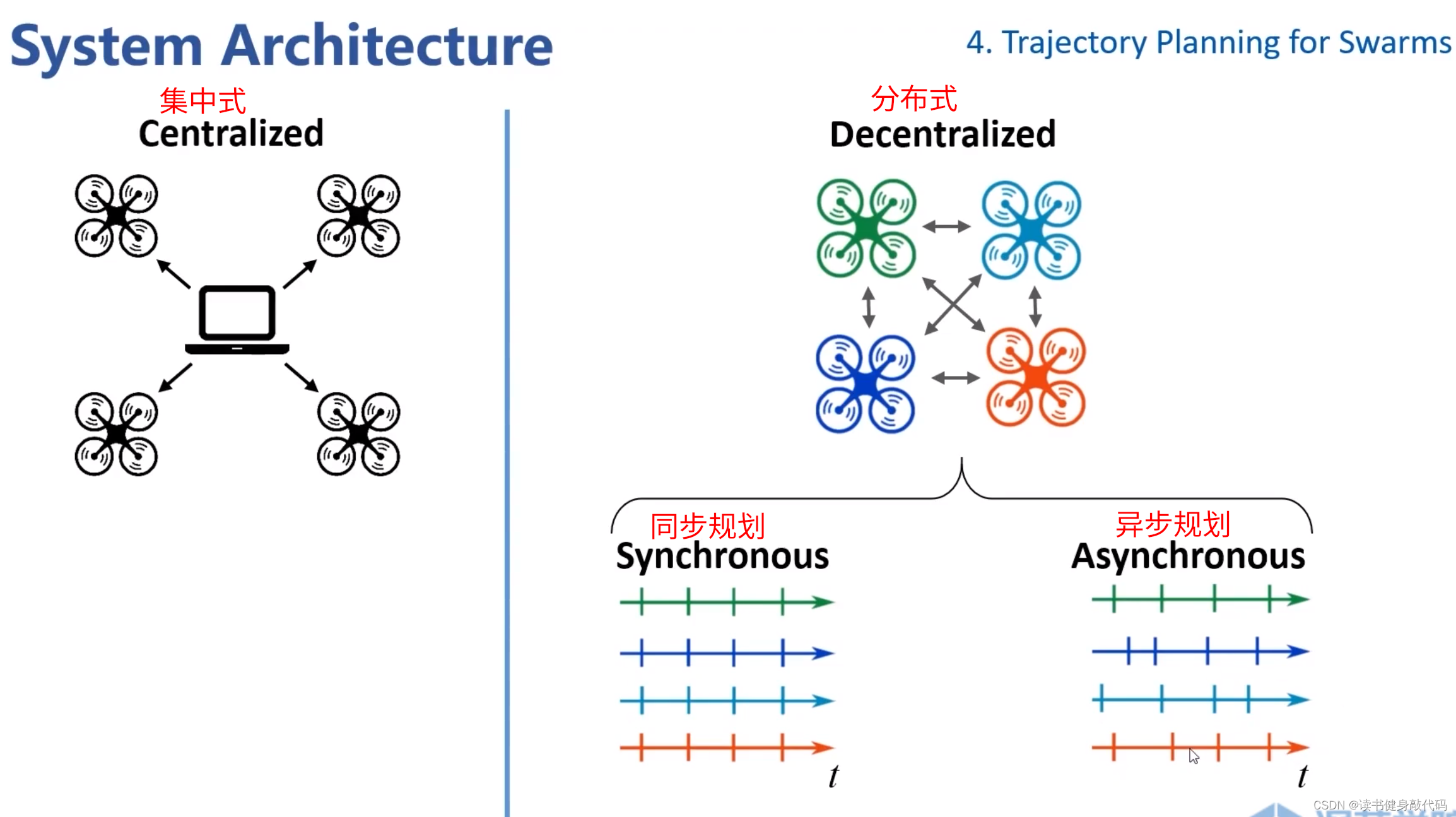
系统结构分为 集中式 和 分布式。
- 集中式:如无人机空中表演,提前算好轨迹发给各个agents执行。
- 分布式:如实时感知并各自进行规划。又分为同步规划和异步规划。
- 同步:按时间触发规划,到时间统一规划。
- 异步:各个agents单独进行感知和规划,同时可以接受各自规划的消息等。(上面ZJU的工作属于这种)
4.2 Methods
4.2.1 Search/Sampling Based
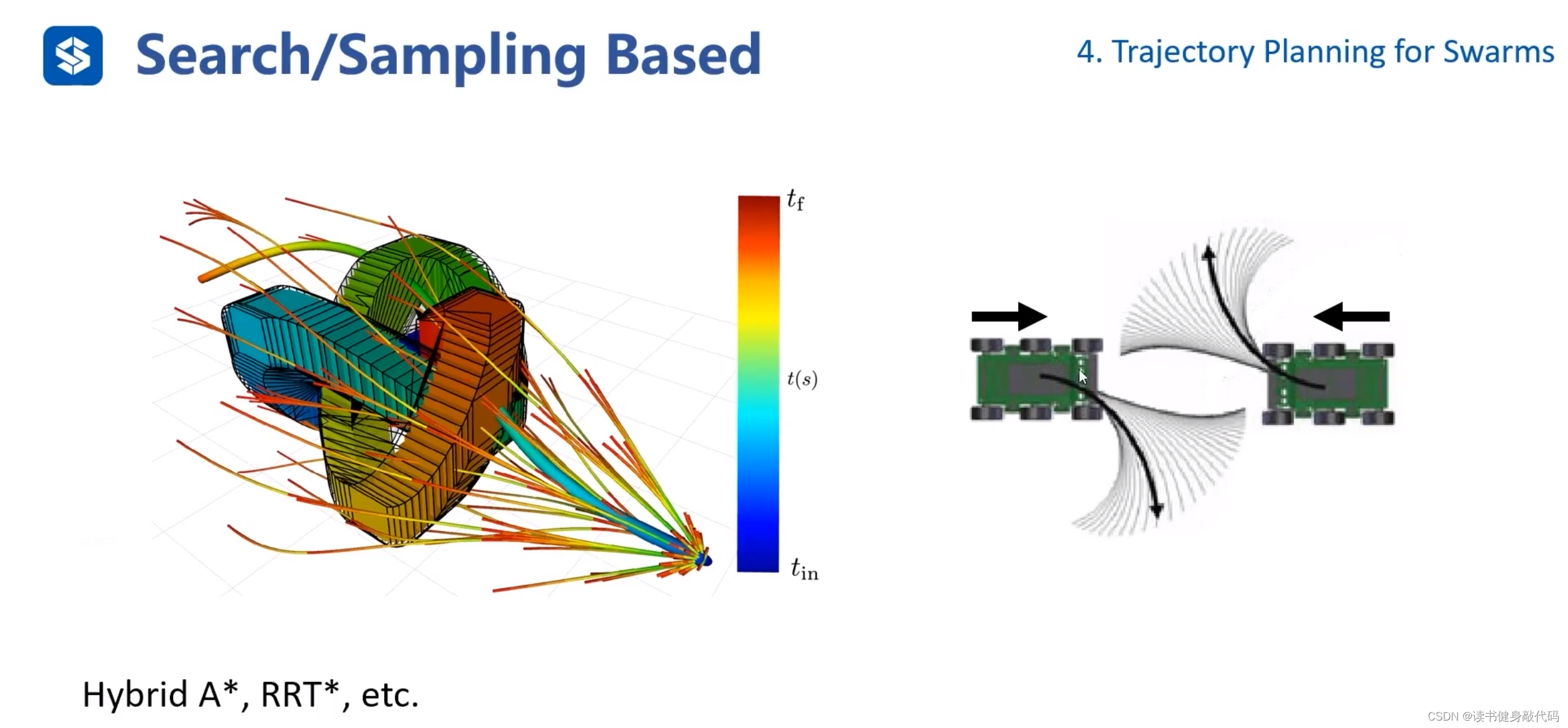
Hybrid A* 是search based method,Kinodynamic RRT*是sampling based method。
- 回顾之前的Hybrid A*(search based kinodynamic planning具体算法)main idea:在control space中sample的lattice graph太过稠密,且采样出的traj不够diverge,一条traj发生collision之后,neighbors也容易发生。结合A*和lattice graph的思想,在lattice graph构建过程中每个grid中只保留一个feasiable connection node,通过一种方法计算计算cost,如果当前grid中node的cost比之前node的小,替换之前的node,此做法称为prune剪枝。
- 右侧对应Kinodynamic RRT*(KRRT*),KRRT* 与传统的RRT* 相比:
- cost不同:RRT使用传统的cost,如欧式距离,KRRT 考虑动力学约束,定义新的cost function。
- 采样方式不同:RRT* 直接采样,KRRT* 需要在full state space中采样,包括p,v,a等。
- near的定义不同:RRT* 寻找x_near只在低维画个圆,在圆内找,圆的半径实际上就是距离采样点x_new的cost相同的流形,而KRRT* 需要考虑高维的near,此处定义距离x_new的cost相同,“半径”取为r rr,引申出正向可达集(forward reachable set,我到哪),反向可达集(backward reachable set,哪到我)。
- ChooseParent和rewire不同:ChooseParent时需要计算backward reachable set(哪到我),进行rewire时需要计算forward reachable set(我到哪)。
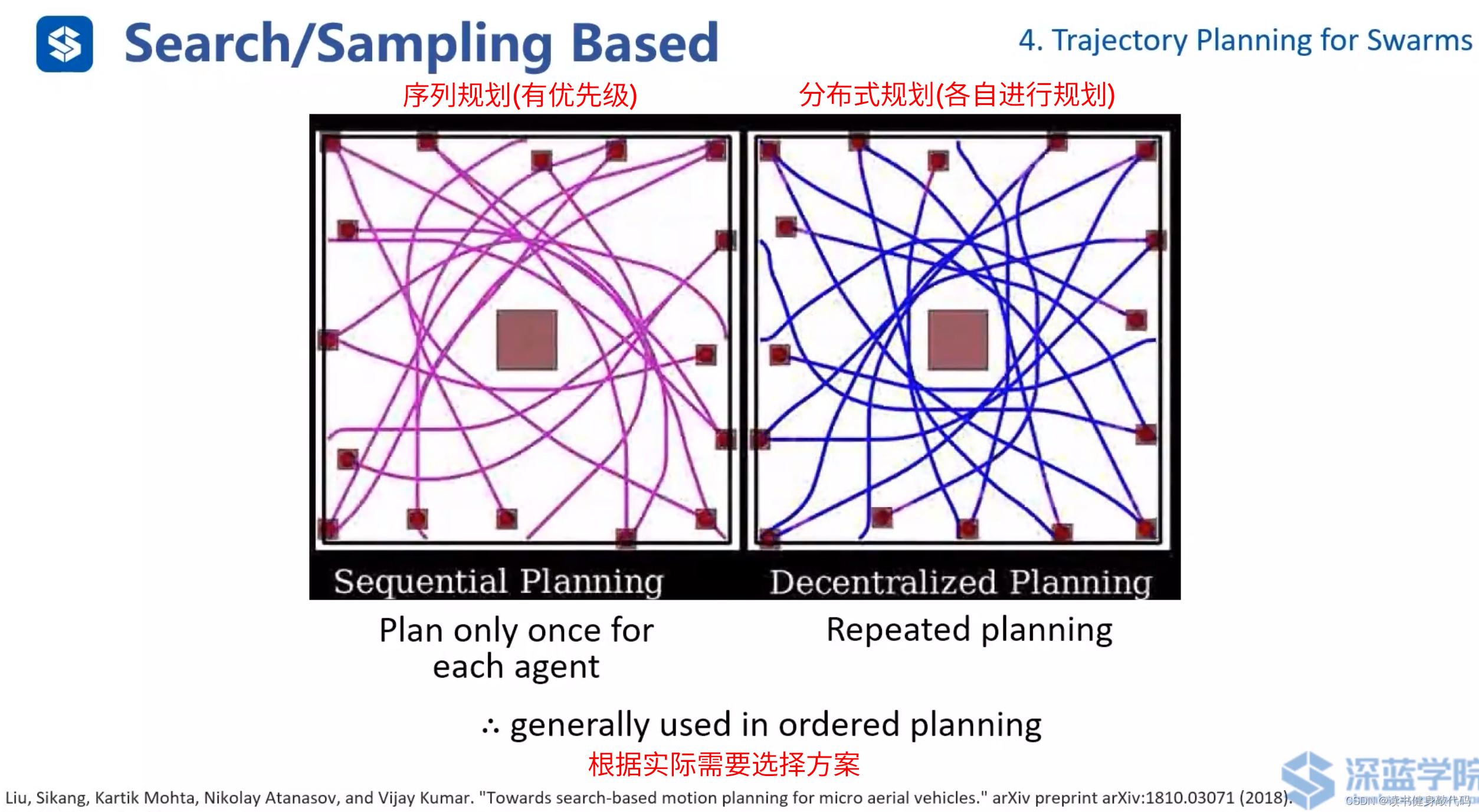
序列规划和分布式规化(ref[13])。
4.2.2 Optimization Based
4.2.2.1 Formulation

基于优化的方法(这里应该指后端),通常是构造cost function,并对其最小化,考虑环境约束,动力学约束,针对集群机器人运动规划,还需要考虑agents之间的碰撞约束。
一个经典的碰撞约束如上图所示构建:
x \bm x x为轨迹的参数, d i j d_{ij} dij是两个agent间的距离, i , j i,j i,j分别是agent的编号,在 [ T 0 , T m ] [T_0,T_m] [T0,Tm]是规划有效的时间范围,约束为
C − d i , j ( t ) ≤ 0 \mathcal{C}-d_{i,j}(t)\leq 0 C−di,j(t)≤0其中, C \mathcal{C} C为clearance,允许两个agents距离的最小值,上式表示两个agents间的距离 d i , j d_{i,j} di,j需要大于 C \mathcal{C} C,即保证不碰撞。
其他类型的约束构造方式这里不做讲解。
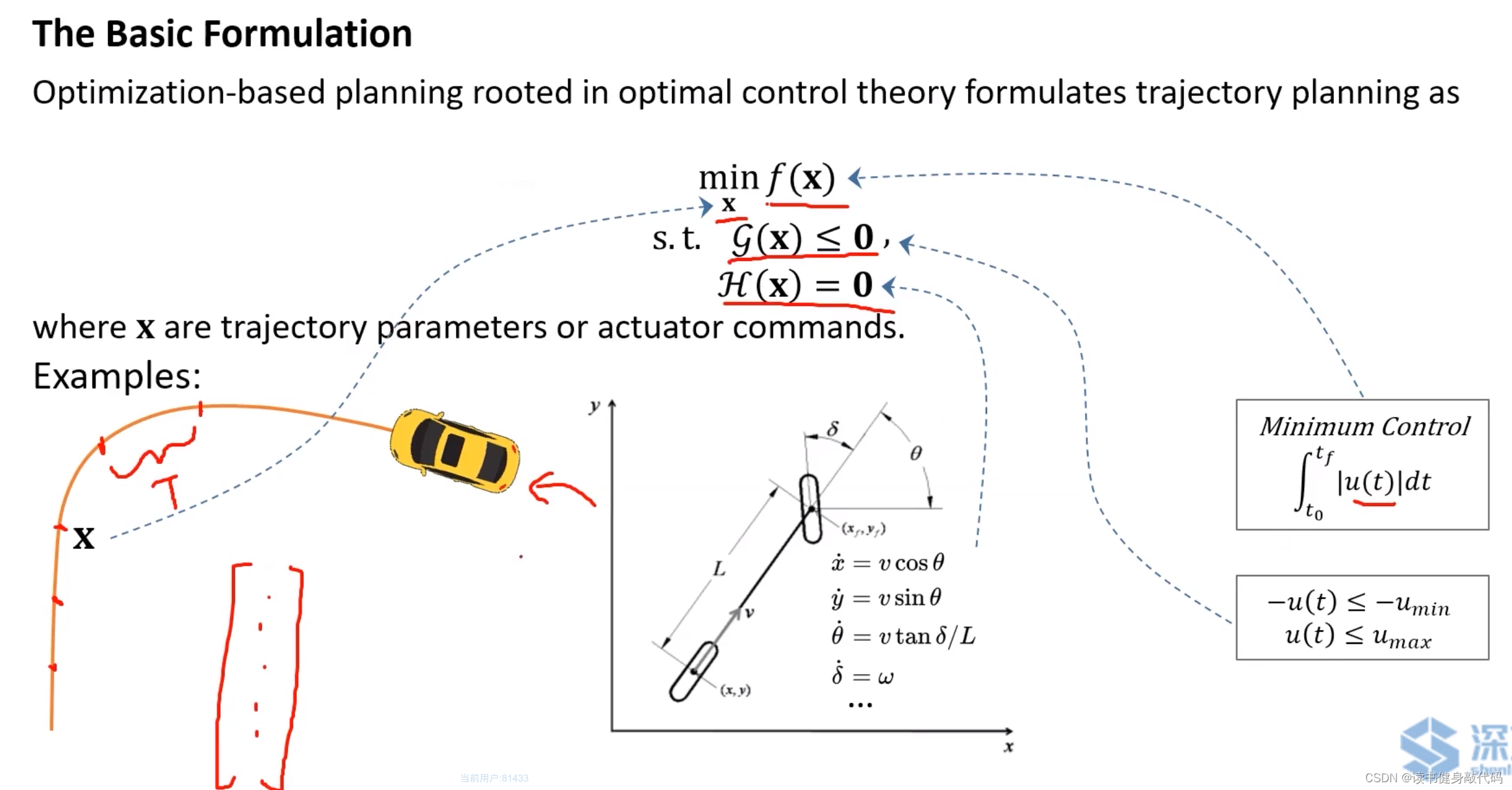
一个简单的例子:
- cont fucntion可以是minimum control的函数(如minimum jerk等)。
- 轨迹参数 x \bm x x可看做一个向量,代表trajectory需要经过的waypoints或者每个piece所持续的时间 T T T。
- 不等式约束如输入最值的约束。
- 等式约束如系统动力学约束。
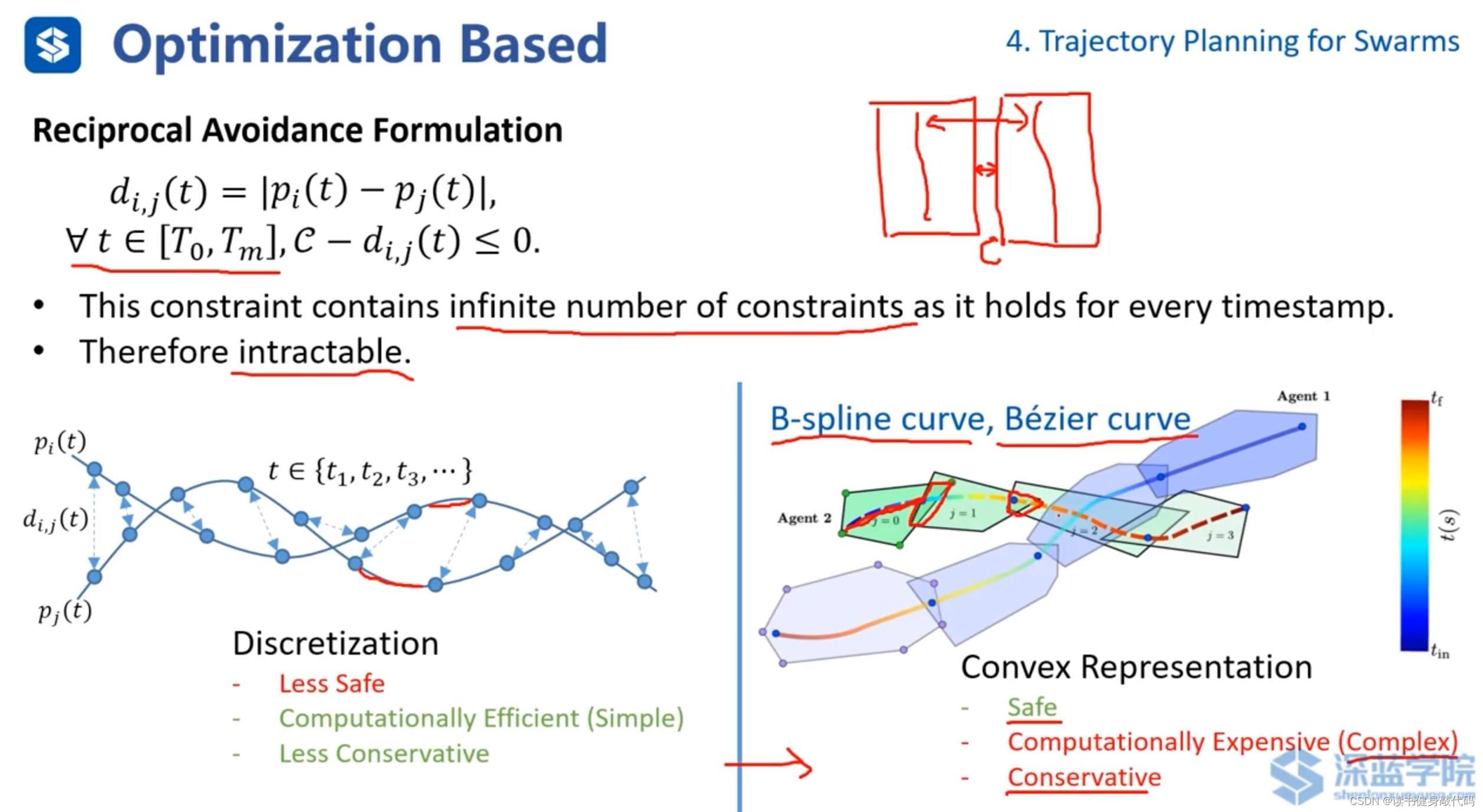
针对前述的避碰约束的构造,由于在 [ T 0 , T m ] [T_0,T_m] [T0,Tm]内的时间有无数多个,而构造无数多个约束对于一个问题而言是无解的,所以有两种方法:
- 离散采样:在各个trajectory上进行离散采样,利用采样点构造避碰约束。
优点:简单,计算效率高;Less Conservative更不保守(相对于Convex Representation方法而言)。
缺点:安全性低。 - Convex Representation凸包表示:使用B样条曲线或者Bezier曲线对轨迹进行凸表示,使用凸多面体进行包裹,计算各个trajectory的凸多面体之间的最小距离,如果大于clearance则不会发生碰撞(计算该距离也是难点,下面会进行讨论)。
优点:安全。
缺点:计算量大;Conservative保守(如上图所示,凸包间的距离已经优化到最小值了,但实际的两条trajectory的距离远大于clearance,实际上trajectory远没有发生碰撞)。
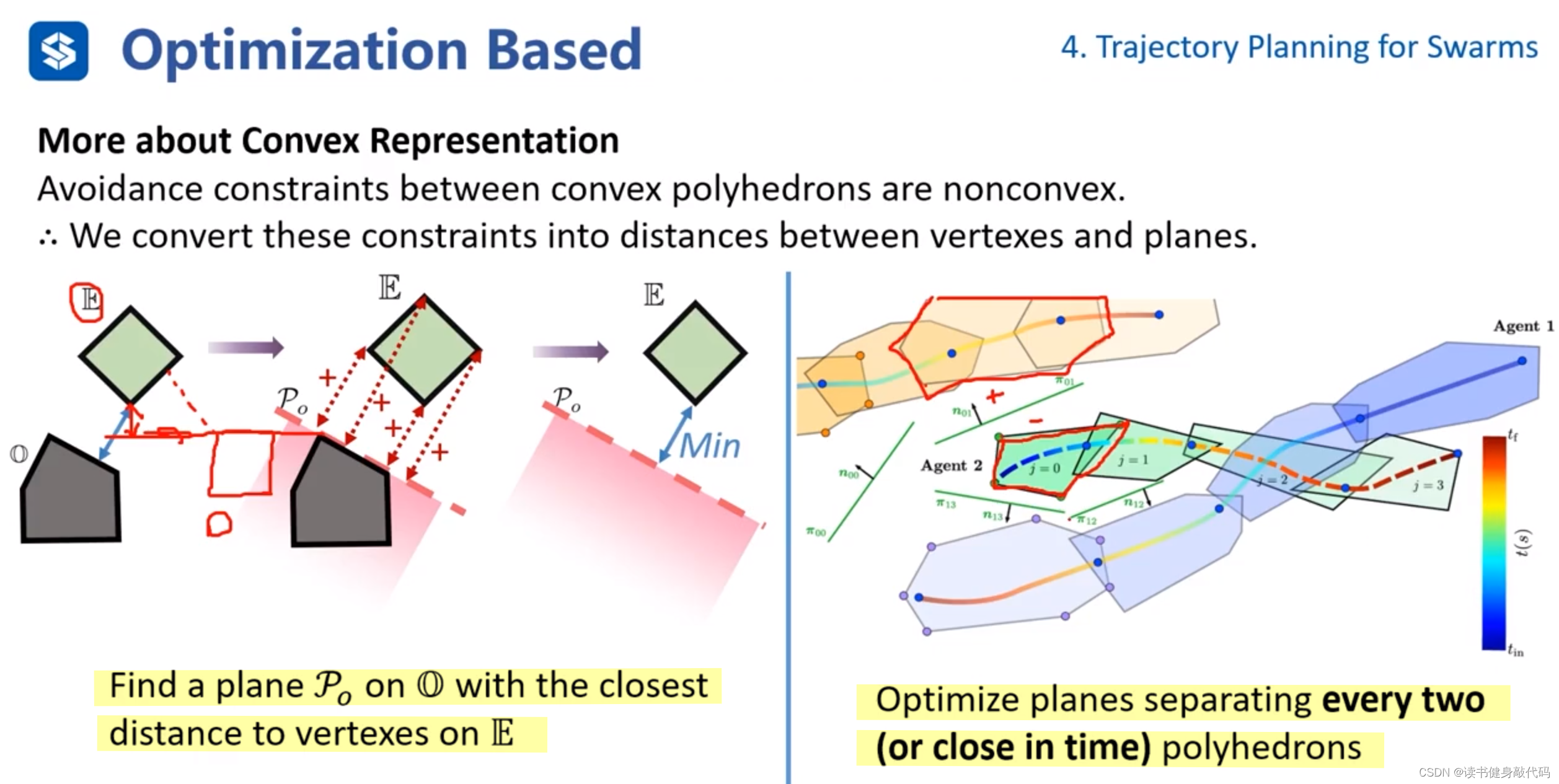
- 法1:在其中一个凸包上找一个平面(平面有方向,平面法线正方侧向为+,平面法线反方向侧为-),计算另一个凸包距离该平面的最小距离作为这两个凸包的最短距离。(该方法不完备,因为如上图左所示,求出的最短距离总比实际的最短距离更短,所以也更保守)
- 法2:分离平面法。在两个凸包间求取一个分割平面(在中间即平面一个方向凸包为+,另一方向凸包为-),使得两个凸包距离分离平面有一定的距离,将平面参数也加入到优化问题中进行优化。为了减少待优化平面的个数,只计算时间接近的trajectory的凸包间的分离平面。
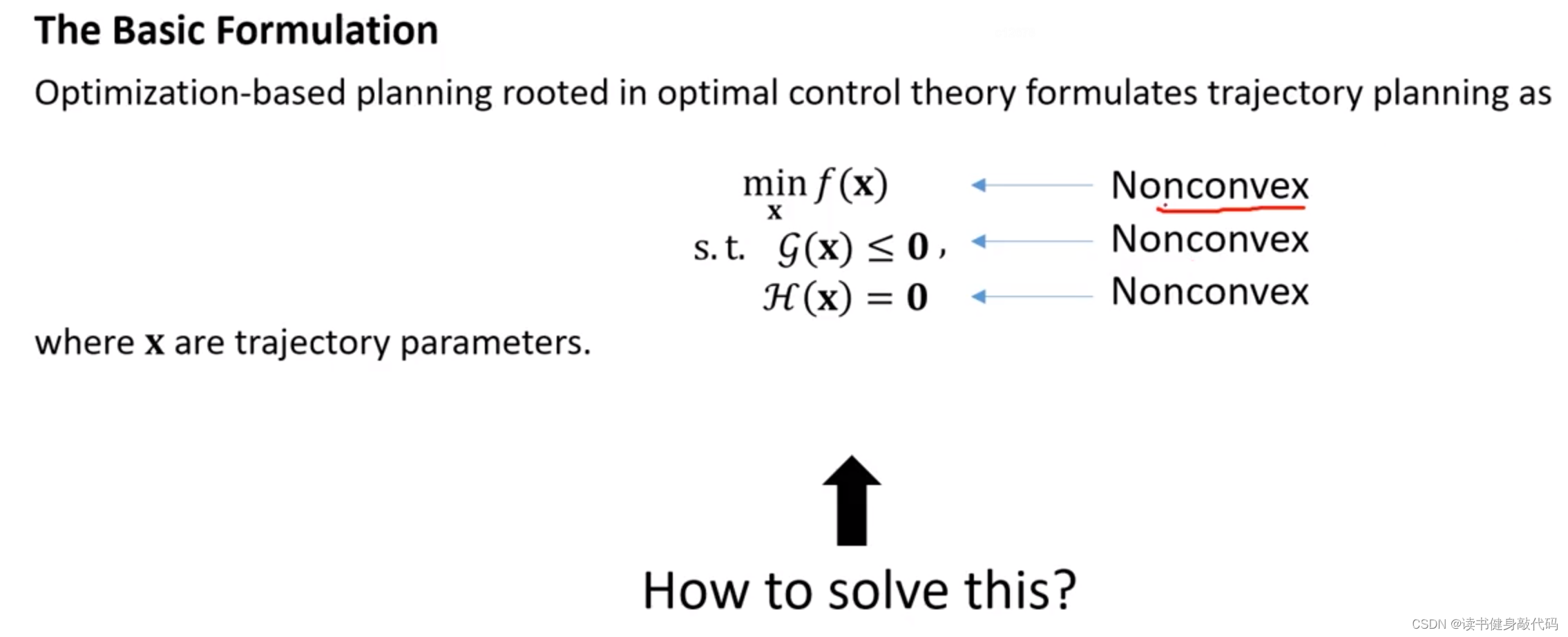
更多时候,问题是非凸的,需要转化,下面介绍两种方法:Sequential Convex Programming和Penalty Method。需要指出,对于general的问题,下面两种方法均不能保证找到全局最优解。
4.2.2.2 Solving

使用"Sequential Convex Programming" (“序贯凸规划”):
序贯凸规划是一种数学优化方法,它用于解决非凸优化问题。这种方法的基本思想是将非凸问题分解成一系列凸子问题,然后顺序地求解这些凸子问题。每次解决一个凸子问题后,都会更新问题的参数,然后解决下一个凸子问题,如此迭代,直到满足某些收敛条件。序贯凸规划在工程优化设计、控制系统、机器学习等多个领域都有应用。
具体到问题:
使用仿射变换(Affine transformation)和凸变换(Convex transformation)
- 对于cost function和不等式约束,使用二阶Taylor展开进行凸变换。
- 对于等式约束,使用一阶Taylor展开进行仿射变换(即转换为Ax+B的形式)。
需要注意,Sequential Convex Programming是有损的。
转化完成之后,可借助 mosek,gurobi等求解器完成求解。

将带约束的问题转化为无约束问题。通过将约束转化为惩罚项加入到cost funtion中进行优化,该方法不保证问题为凸问题,通过迭代数值求解(如G-N,LM等),得到local minimum。
- 把不等式约束转化为等式约束,数学上喜欢 G ( x ) + s 2 \mathcal{G}(\bm x)+\bm s^2 G(x)+s2以保证连续性,而工程上常使用 m a x ( G ( x ) , 0 ) \mathop{max}(\mathcal{G}(\bm x),0) max(G(x),0)
- 为等式约束和不等式约束分别添加权值 μ 1 , μ 2 \mu_1,\mu_2 μ1,μ2,随着迭代的进行,不断增大权值,使得约束收敛至0。要求从较为合适的初值( x ( 0 ) , s ( 0 ) \bm{x}^{(0)},\bm{s}^{(0)} x(0),s(0))开始迭代。
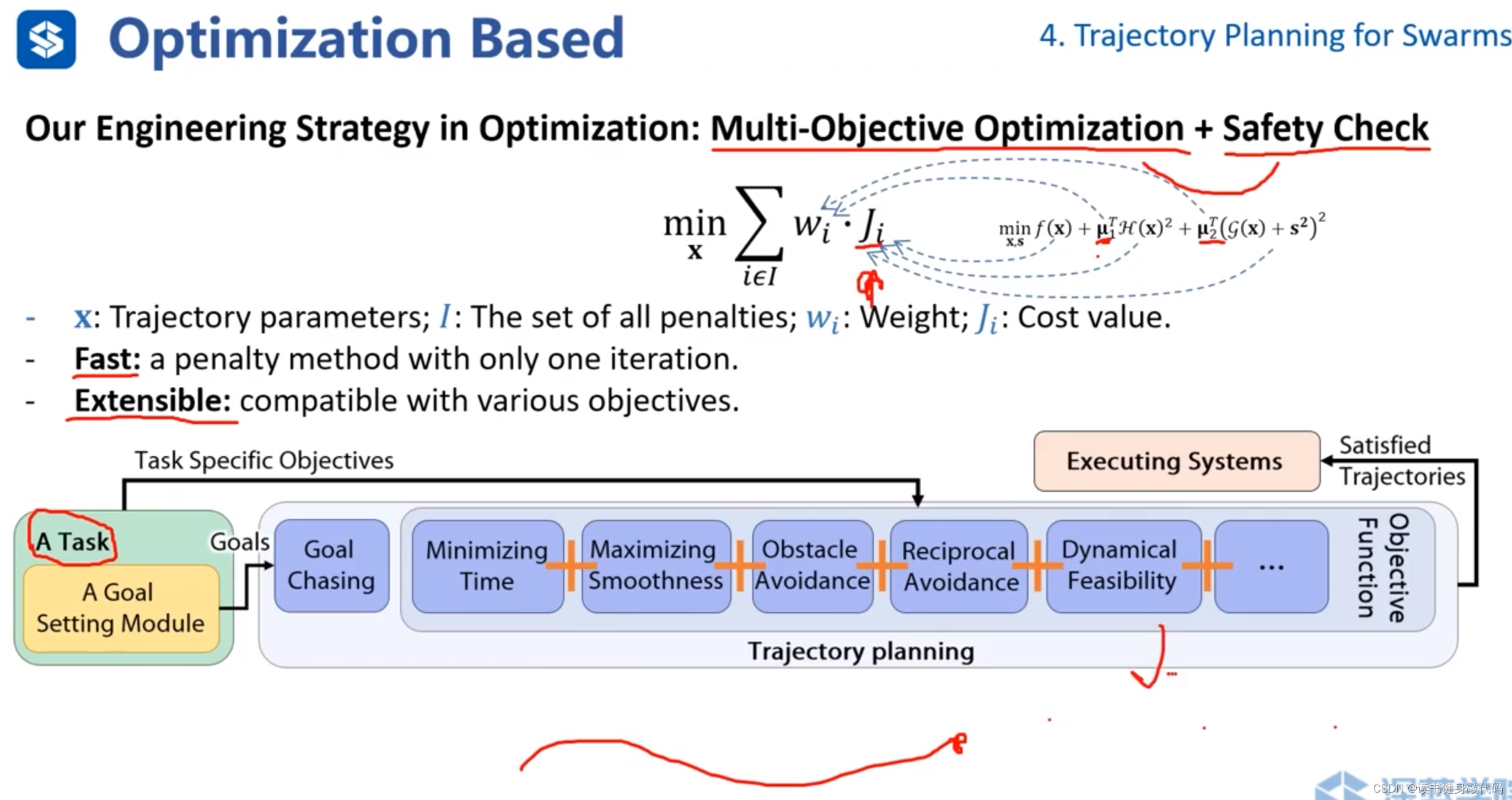
ZJU的工作(偏工程的方法)
转化为“多目标优化问题+safety check”的框架。(类似于Ch4作业中的ref[1]的动力学约束的多旋翼轨迹生成的框架)
权值 μ 1 , μ 2 \mu_1,\mu_2 μ1,μ2事先给定,在优化过程中不进行调整。
整个框架先生成轨迹再进行safety check。把cost fucntion和各种约束都转化为 ω i ⋅ J i \omega_i \cdot J_i ωi⋅Ji的形式,整个框架不断地生成一小段一小段轨迹,goal不断往前移动。
框架优点:1. 快速;2. 可拓展(新的约束也可转化为 ω i ⋅ J i \omega_i \cdot J_i ωi⋅Ji的形式)
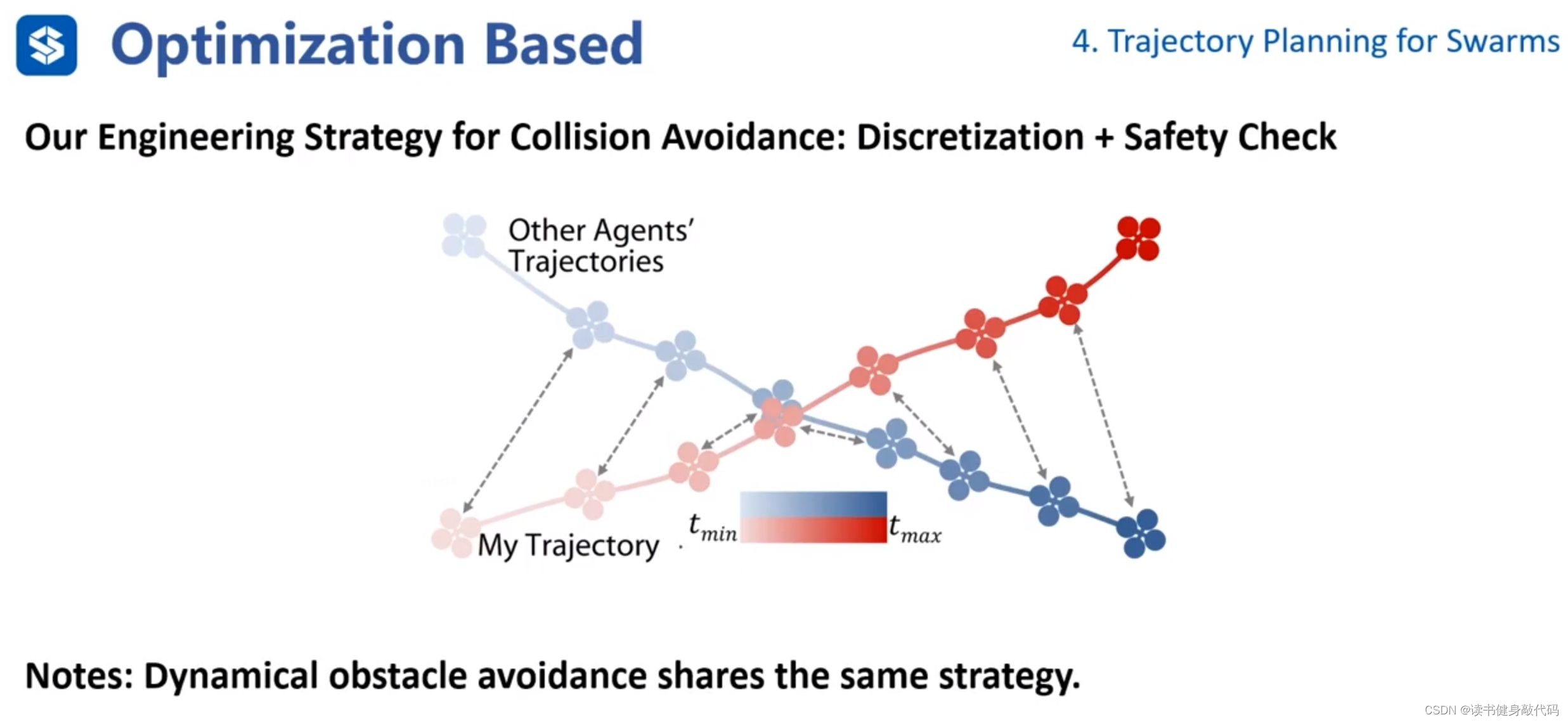
关于多个无人机如何避障,使用采样的方式,通过safety check保证安全,采样点处安全即可。多个无人机可以共享相同策略。
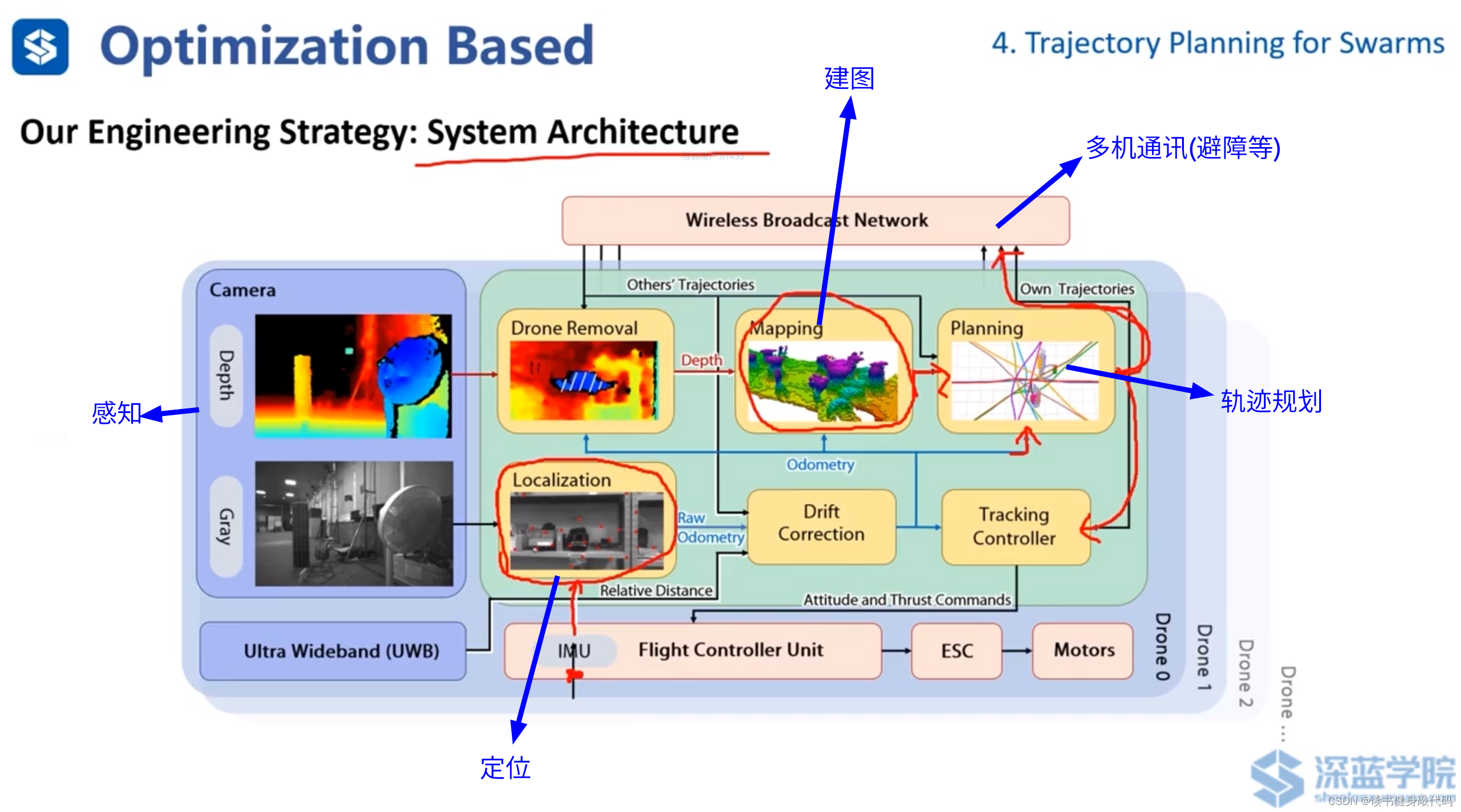
ZJU工作的整个系统框架,发表于Science Robotics期刊,ref[16]。
5. Formation(编队)
在运动规划领域中,“formation” 通常指的是一组自主体(可以是机器人、无人机、车辆等)按照某种特定的空间排列进行移动。这种排列可以是为了各种目的,比如提高效率、增强稳定性或者完成特定的任务(如搜索和救援、军事编队、农业作业等)。
有序的"formation"有助于协调集体行动,确保安全距离,提高集体感应能力,并且可以根据环境或任务需求动态调整。在设计这样的系统时,需要考虑个体之间的通信、同步、避障和路径规划等问题。
Formation通常和数学联系较为紧密。
5.1 Preliminary

首先介绍拉普拉斯矩阵:
- 定义无向图 G = ( v , ϵ ) \mathcal{G}=(\mathcal{v},\epsilon) G=(v,ϵ), v v v顶点和 ϵ \epsilon ϵ边。
- 度矩阵 D \bm D D是对角阵,对角线元素是各顶点边的权值之和。
- 邻接矩阵 A i j \bm A_{ij} Aij:主对角线为0,上下三角分别是对应边的权值。
- 拉普拉斯矩阵 L = D − A \bm L=\bm D-\bm A L=D−A, D \bm D D和 A \bm A A没有实际的数值计算,都是与0加减,主对角线元素是该列其他所有元素之和的相反数。
5.2 Consensus-based Control(基于共识的控制)
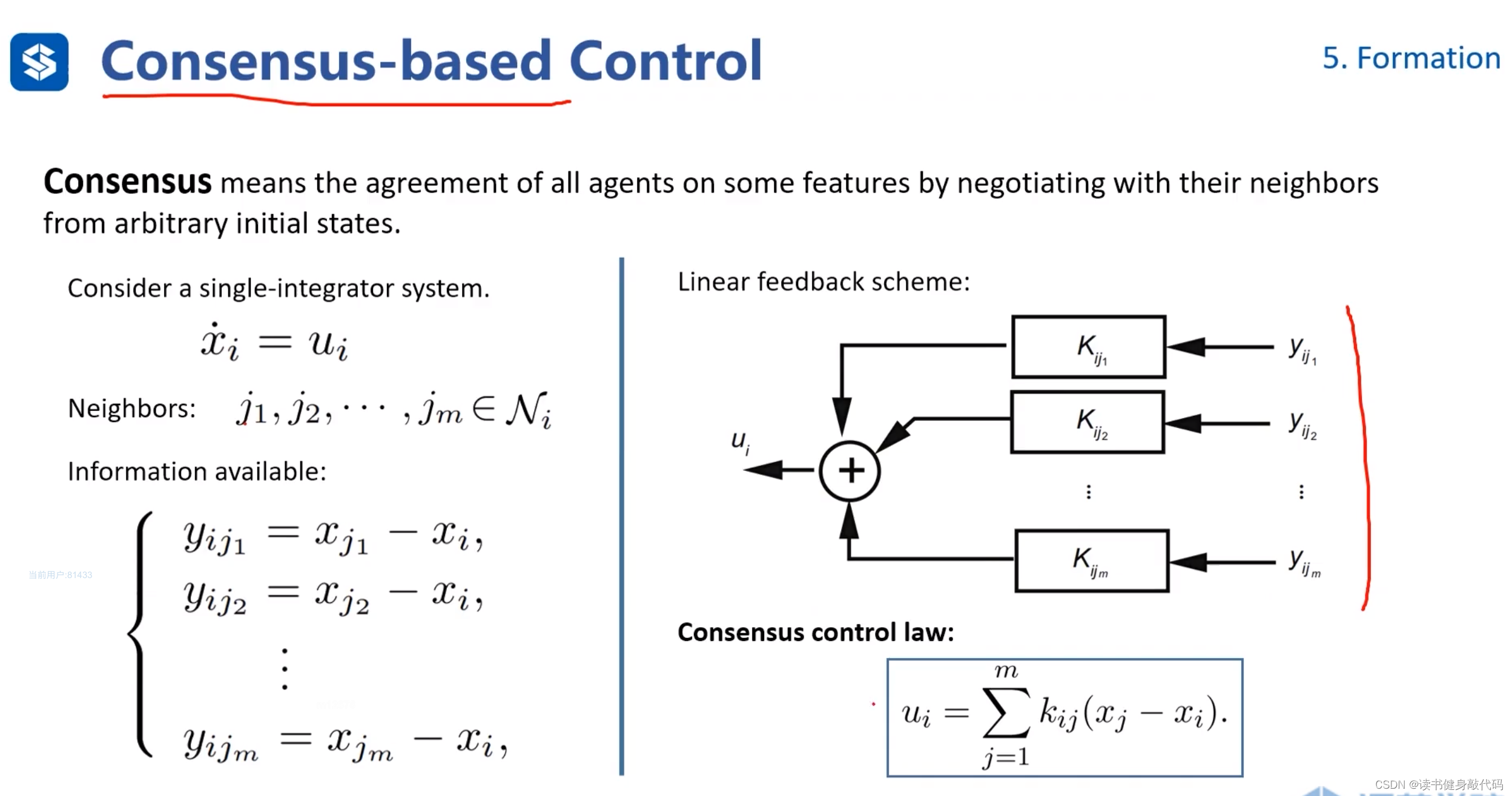
对于单积分系统 x i ˙ = u i \dot{x_i}=u_i xi˙=ui,
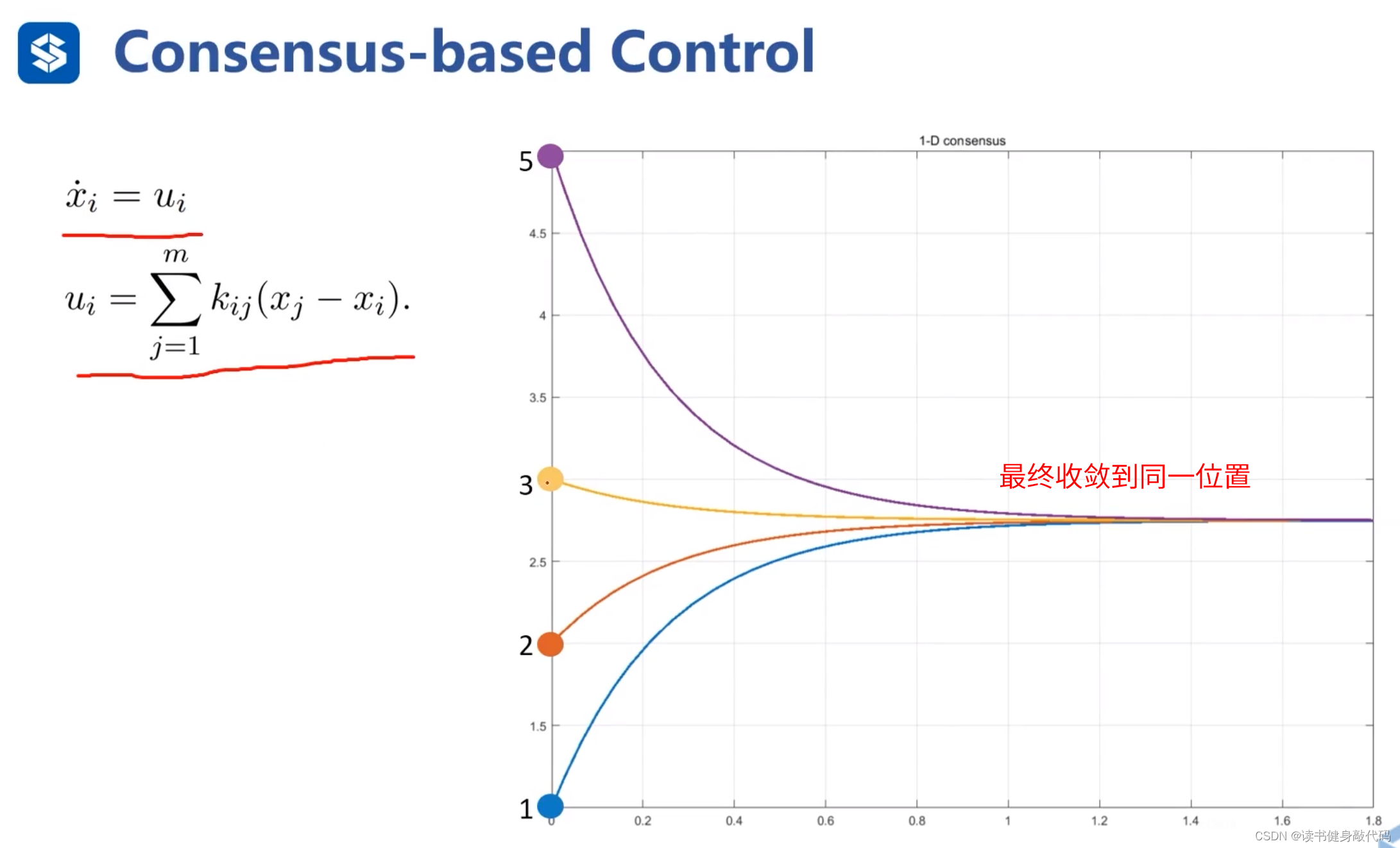
定义反馈量 y i j y_{ij} yij,表示 x i x_i xi周围的邻居agents分别到我的距离,最终目的是让所有邻居agents汇聚到同一点,可以证明这种控制规则是收敛的。
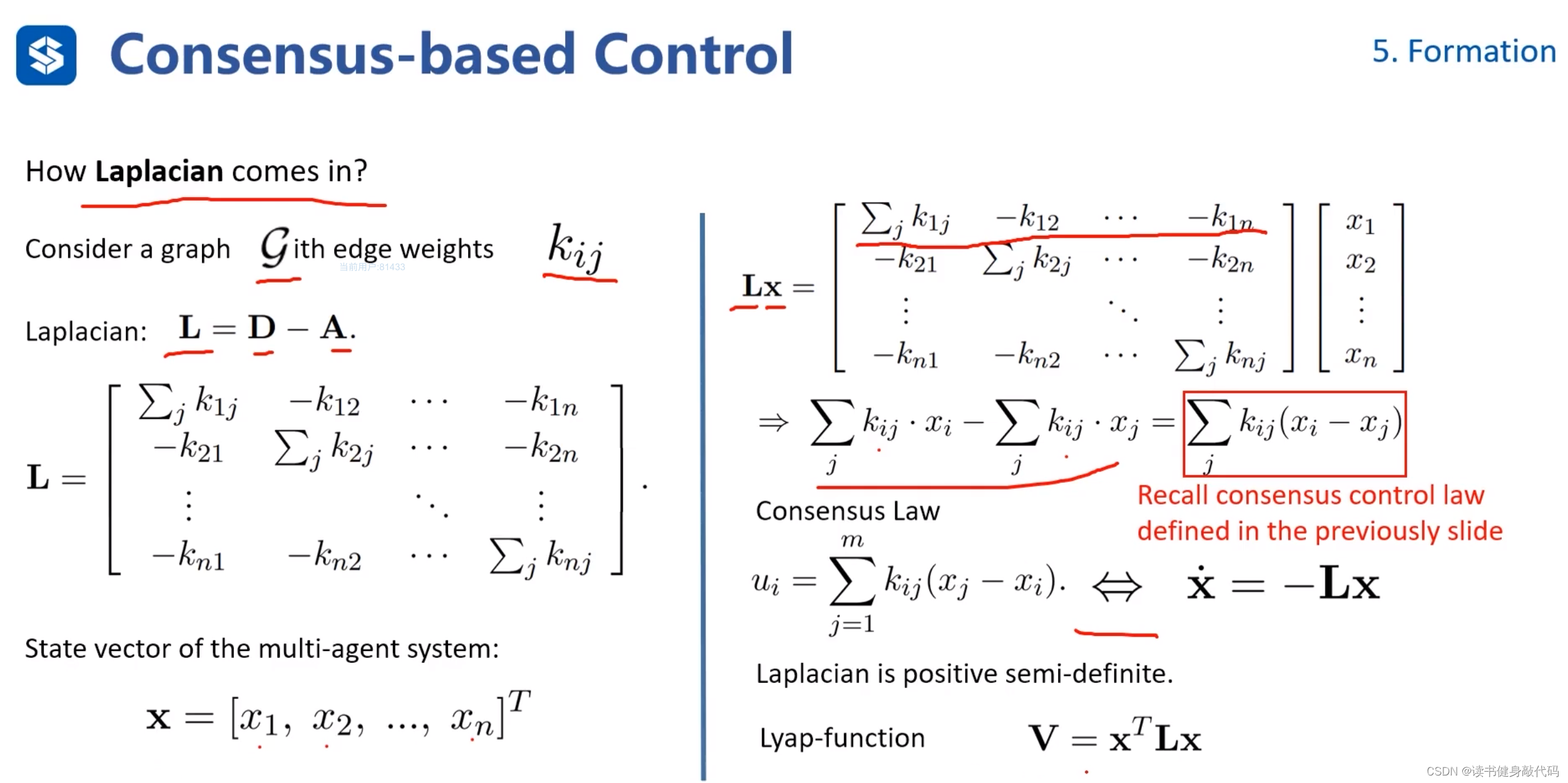
将Laplacian Matrix与状态量相乘,我们发现相乘结果和前面定义的Consensus control law非常相似
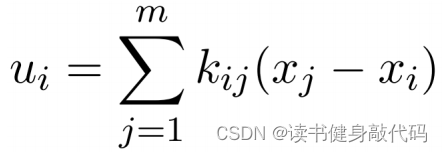
所以系统方程可整理为
x ˙ = L x \bm{\dot{x}}=\bm L \bm x x˙=Lx
可构造典型的李雅普诺夫函数 V = x T L x \bm V=\bm x^T \bm L \bm x V=xTLx该函数是半正定的。
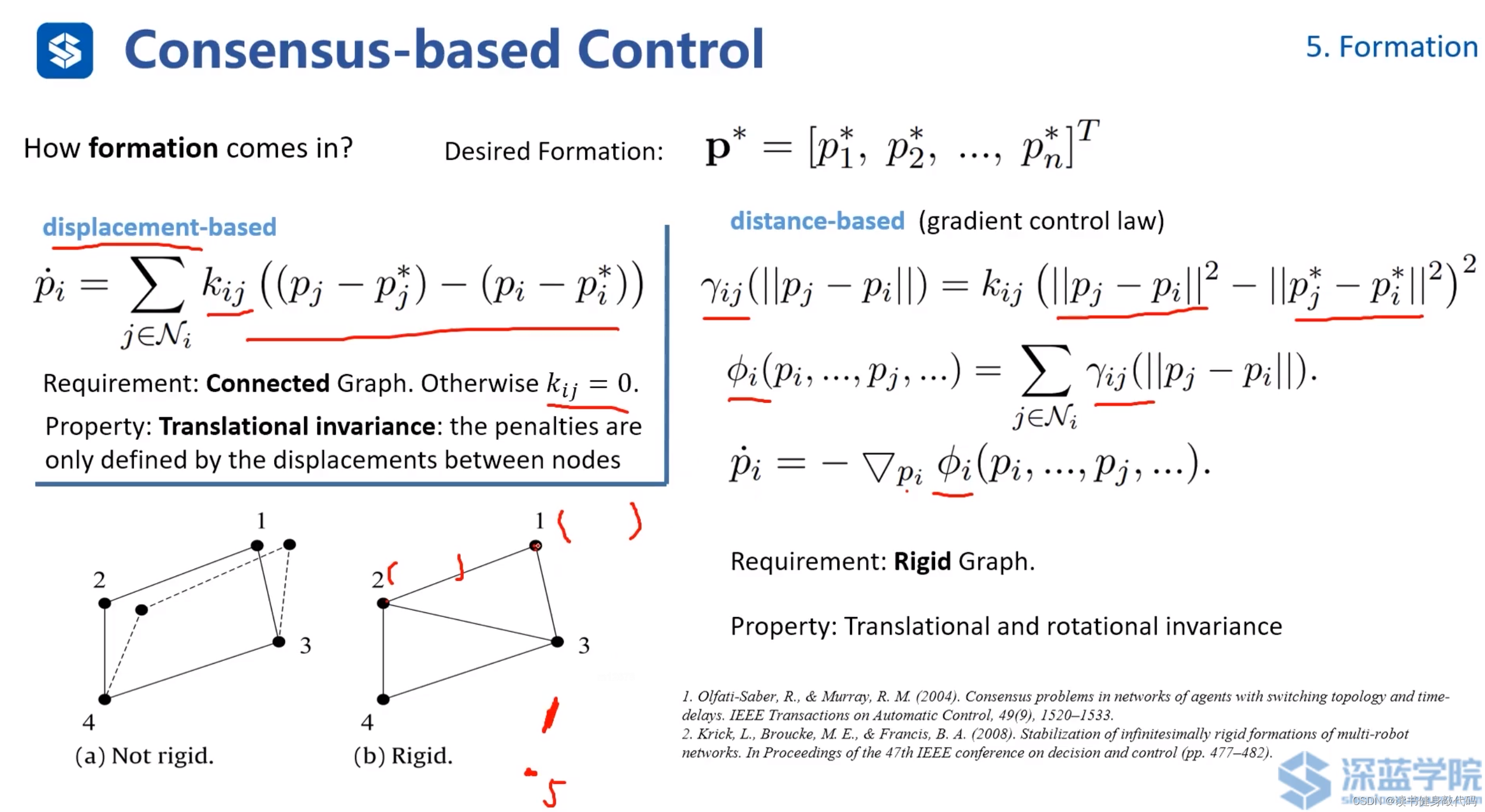
编队的构造,讲两种方法:
- 基于偏移的编队(ref[14]):为每个agent增加,一个平移偏移,最终为每个agents添加的偏移就成为了队形。
要求:图是connected的,即没有孤立的节点。
特性:Translational invariance,整体平移并不改变队形。 - 基于distance的编队(ref[15]):根据其他agents到该agents的距离二范数构造 γ i j \gamma_{ij} γij,将所有agents的 γ i j \gamma_{ij} γij求和,构造目标函数,分别对各个agents求偏导得到一阶导数,然后可以使用数值优化等方法(G-N等)求解。
5.3 Potential Field
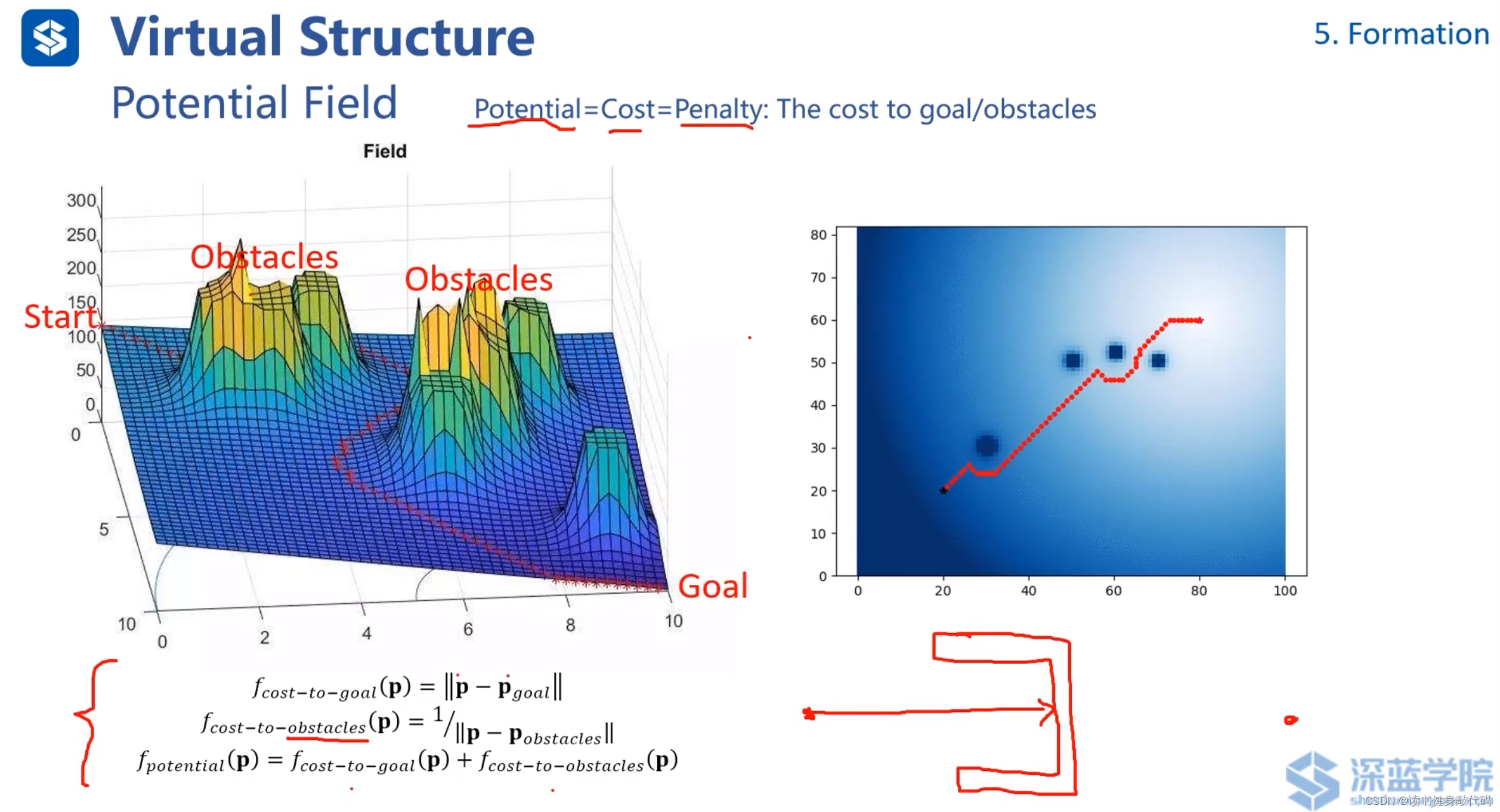
Potential Field 势场法:是一种用于路径规划和避障的数学模型和算法,它通过模拟物理世界中的电磁场或重力场的概念来引导机器人或者其他自主体从起点移动到终点。
在势场法中,目标位置被赋予吸引势能,而障碍物则被赋予排斥势能。移动的自主体(如机器人)被看作是在势能场中的一点,它会受到力的作用,这些力是由其在空间中的位置所处的势能梯度产生的。通过这种方法,自主体被势能场引导,同时尽可能避开障碍物,最终到达目的地。
上图的f也就是potential=cost=penalty, f c o s t − t o − g o a l f_{cost-to-goal} fcost−to−goal代表从当前位置到达goal所需的cost, f c o s t − t o − o b s t a c l e s f_cost-to-obstacles fcost−to−obstacles代表距离障碍物的cost,距离障碍物越近,该项越大。
该方法的一个缺陷是容易陷入local minimum,如上图的U形障碍物所示。
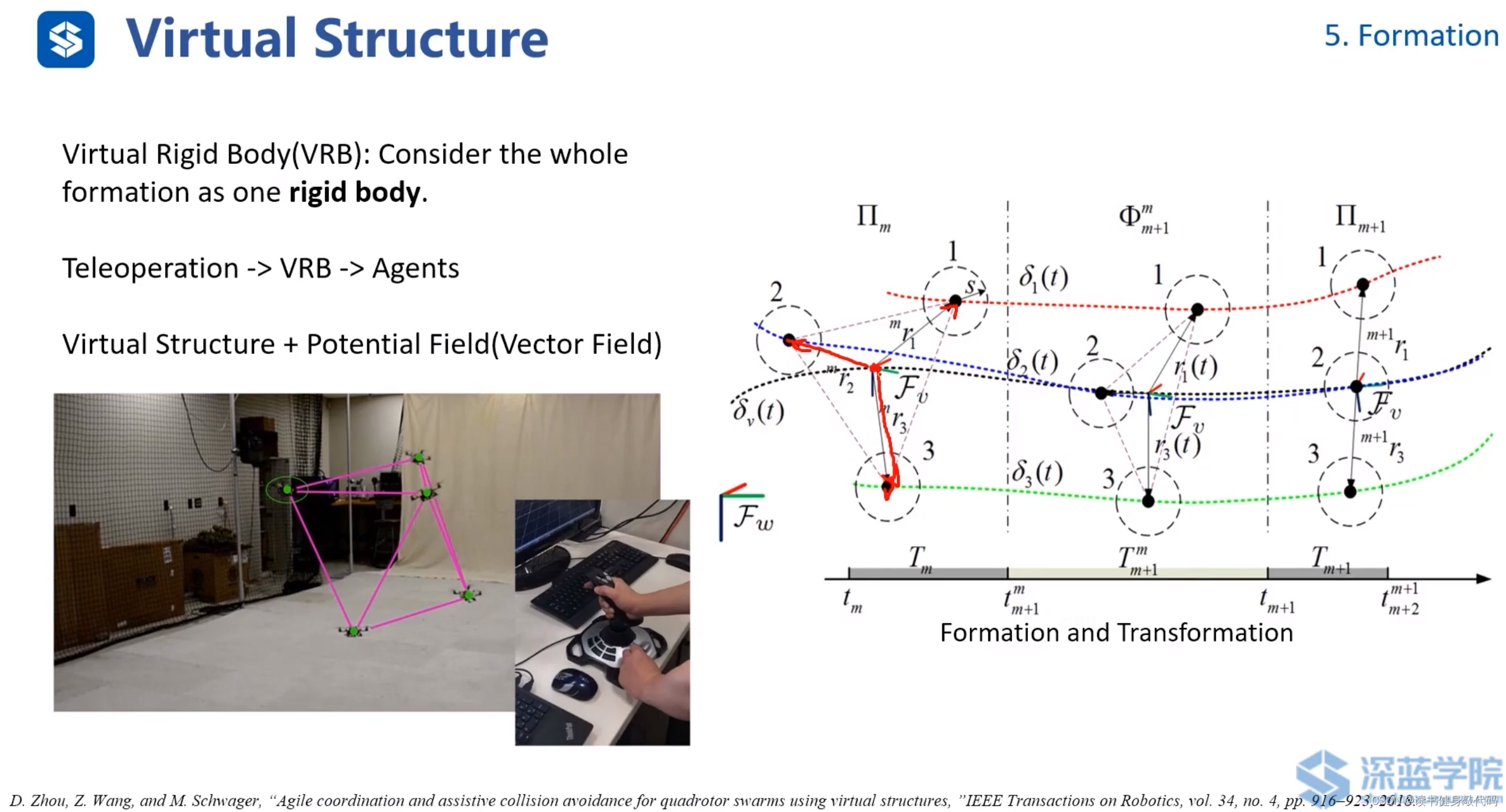
虚拟刚体VRB,不是直接操纵无人机,而是操纵虚拟的formation的中心,ref[17]。
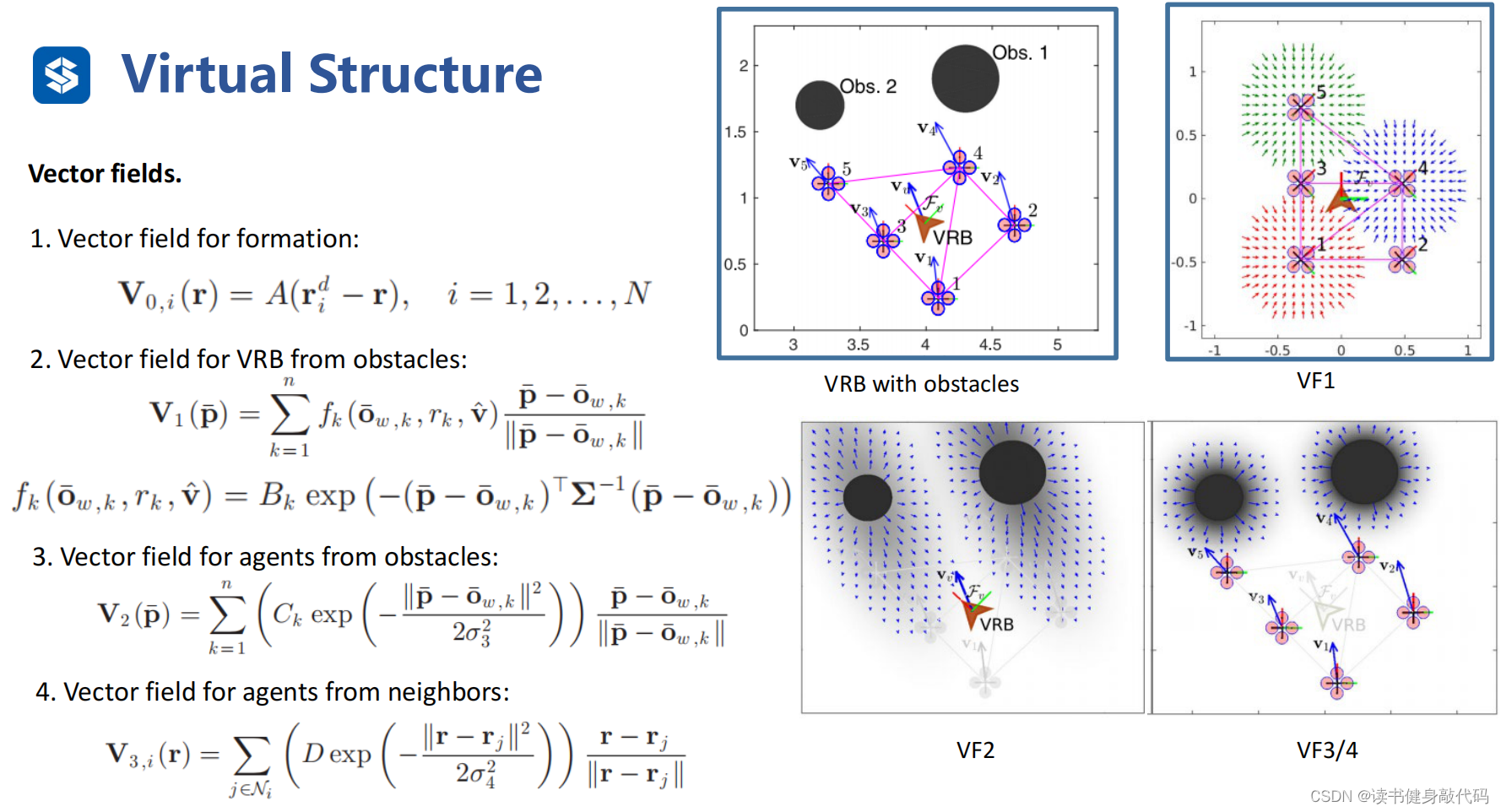
该方法的势场(VF)由4部分组成:(公式可以不用仔细理解,需要时再看,此处仅做定性说明)
- VF1:Formation的势场,如果势场的中心发生偏移,该势场会把中西往回拉。
- VF2:障碍物势场,该势场有方向,沿着速度方向,势场较大,垂直速度方向势场较小。
- VF3:agents到障碍物的势场,大小均匀。
- VF4:agents之间的势场,避免agents之间发生碰撞。
该方法和flocking model非常相近,特点也是对参数较为敏感,如果调参不好可能震荡或者整个formation发散。
5.4 Shape Vector
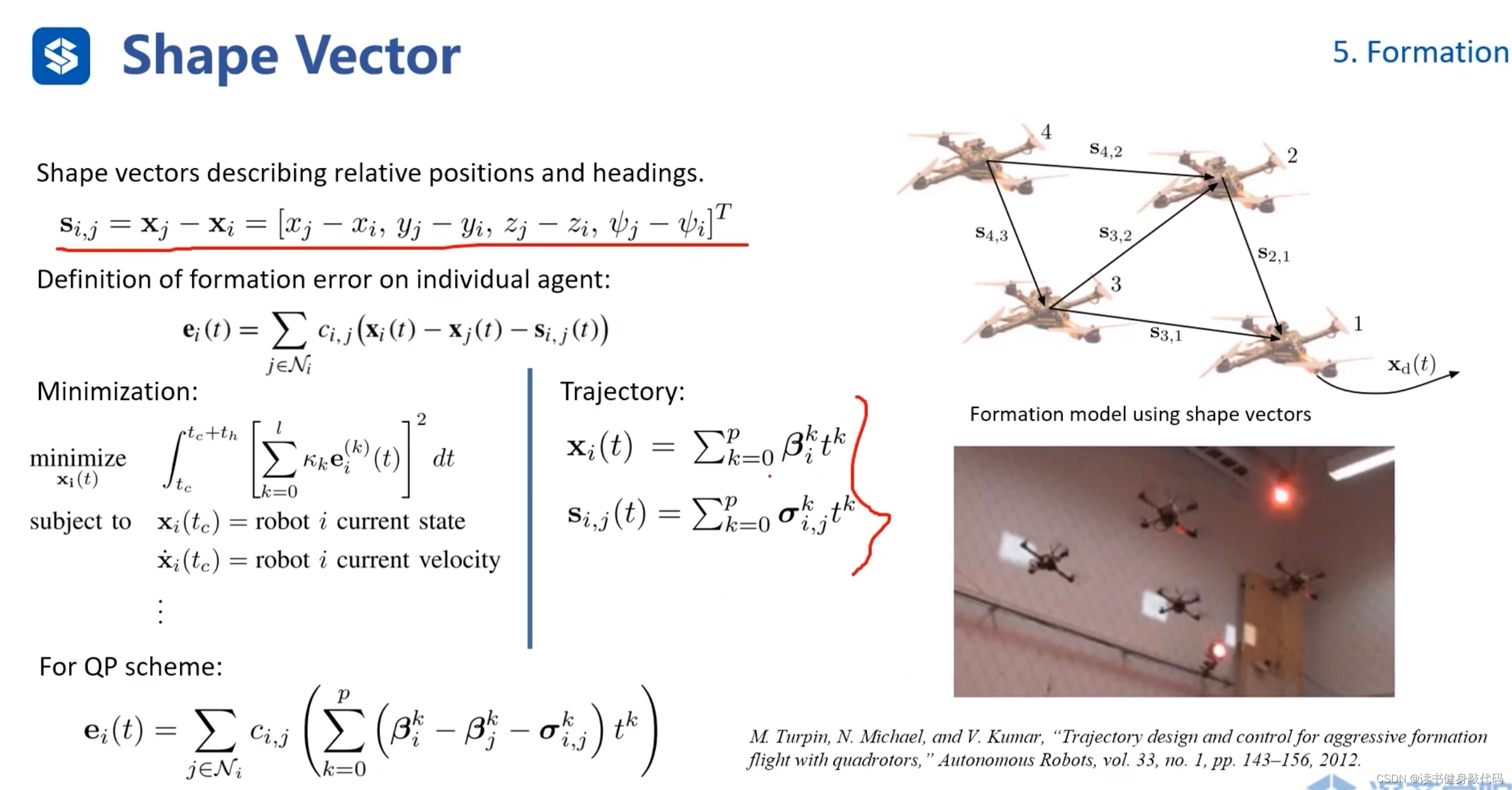
主要是定义方式上的差别,此处state定义为各个agents之间的位置和yaw角的差,然后把问题Formulation为QP问题进行求解,最终的trajectory的 x ( t ) , s ( t ) x(t),s(t) x(t),s(t)均为多项式。(ref[18])
5.5 Formation Rearrangement
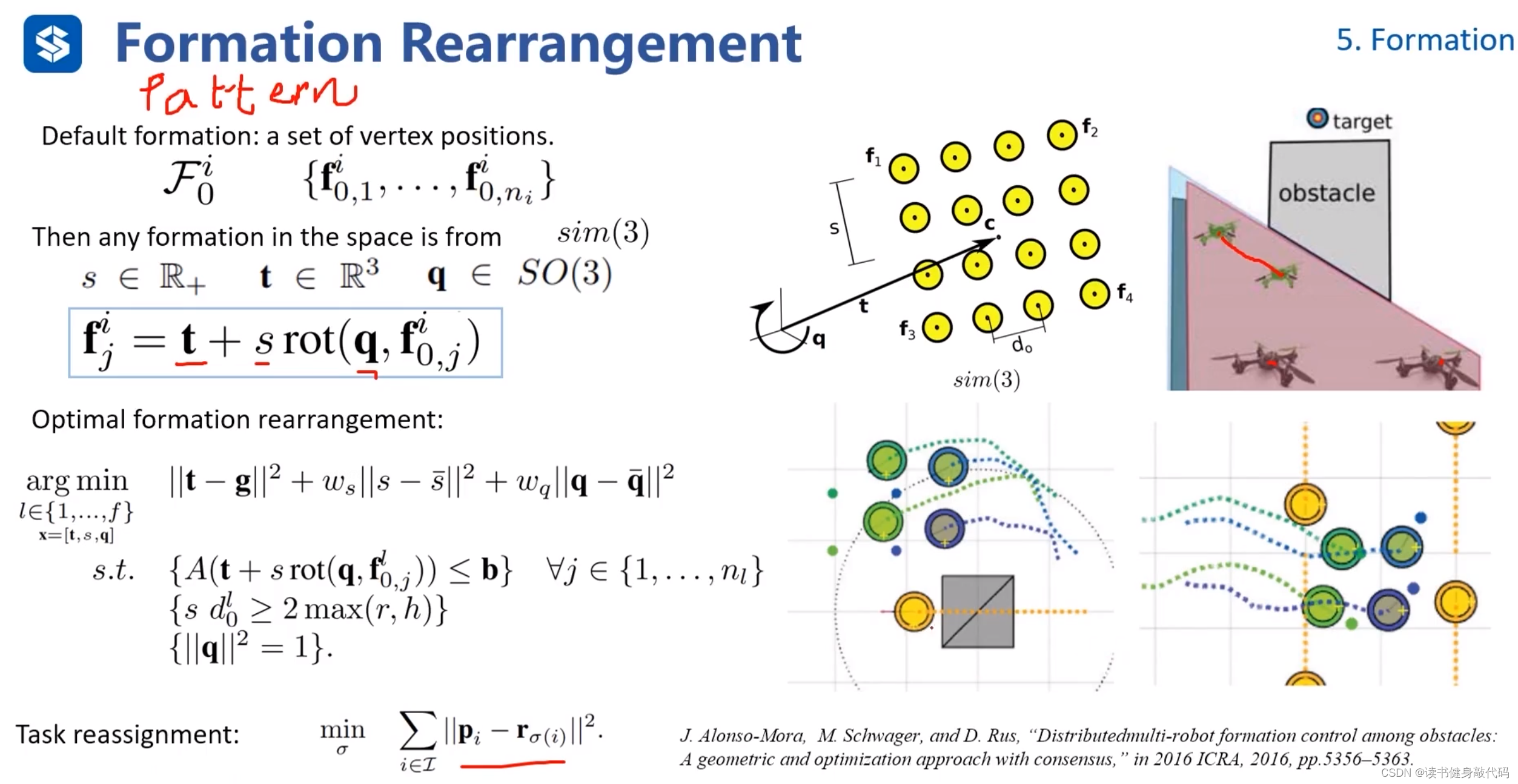
ref[19]
讲的不太清楚,大致思路是:
把formation当做pattern,有了一个新的pattern,思考如何调整旋转q,平移t,缩放s,来使得当前的pattern满足新pattern。
中间的arg min是在定义一个调整上述q,t,s的优化框架,
task assignment是一个优化问题,指的是在formation过程中,所有的agents都是等价的,并不care哪架飞机在哪里,只考虑通过什么分配方式使得变为新formation整体的cost最小,该问题可使用旅行商问题等方法来求解。
5.6 Similarity Metric(相似性度量)
用于评估两个运动、路径或配置之间的相似度(ref[20])
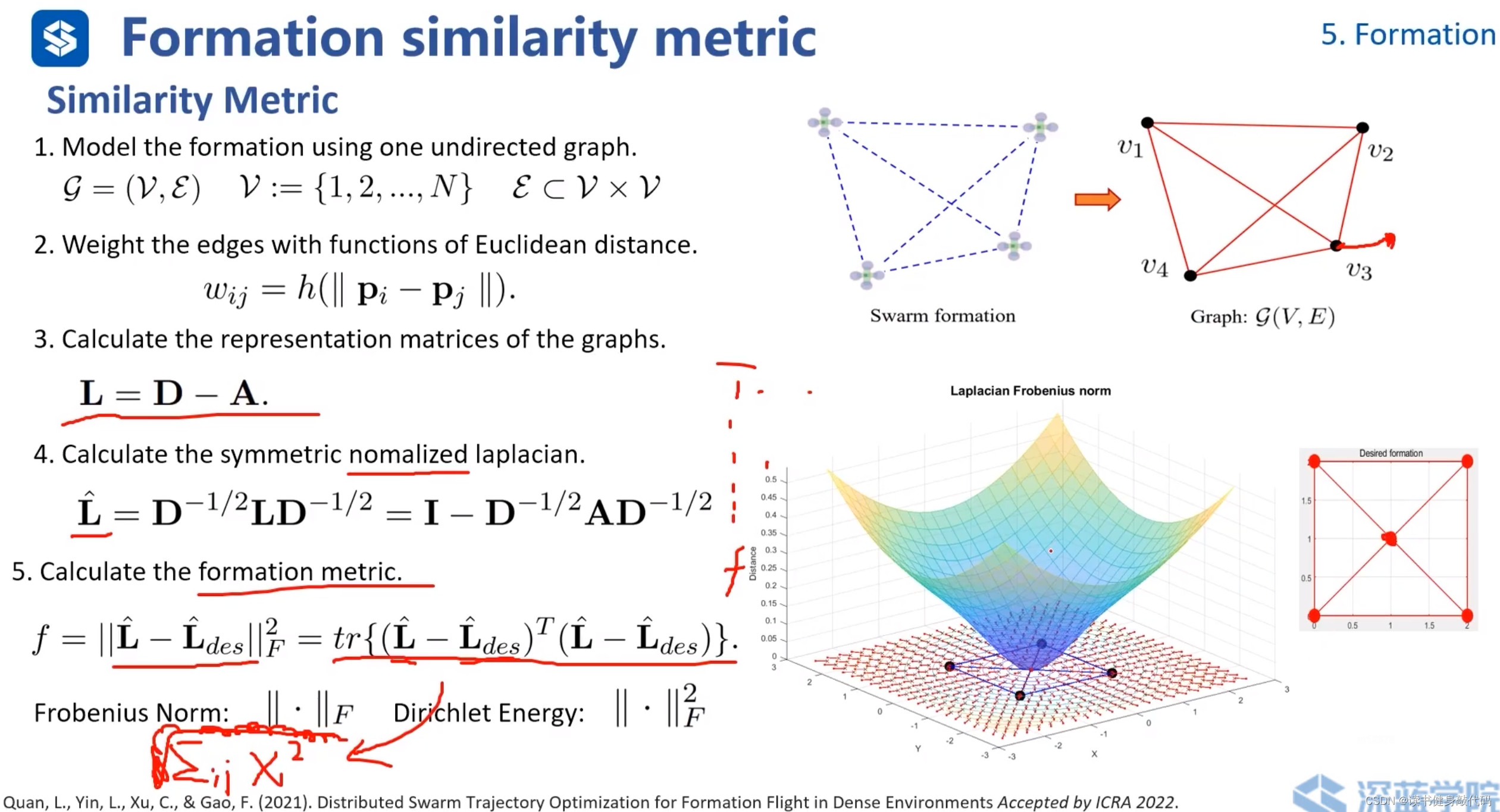
- formation以图的形式表示。
- 以每个agents之间的欧氏距离作为图的边。
- 计算拉普拉斯矩阵。
- 对拉普拉斯矩阵进行归一化,目的是降低由于主对角线元素数量级的差异而带来的矩阵问题,避免某些大元素dominate整个矩阵。(使对角线元素变为1,剩下元素按照上图第4点所示进行变换)
- 计算相似性度量指标 f f f, L ^ \bm{\hat{L}} L^为实际formation的拉普拉斯矩阵,期望的formation也可表示为图的形式, L ^ d e s \bm{\hat{L}}_{des} L^des为期望的formation的拉普拉斯矩阵,二者作差求F范数的平方,即某个运算的迹(数学可证明)。
上图右侧彩图表示已有4个agents,关于第5个agent位置与 f f f的图,可以看出,梯度都向外,按照梯度下降的准则,第5个agent最终落在正中间的才能使得 f f f最小,即与desired formation最相似。
方法特性:
- 平移,旋转,缩放不变性
- translation invariance:在5.2节已经讲解过平移不变形。
- rotation invariance:基于距离的formation对于ratation也是存在不变性的。
- scaling invariance:由于之前对拉普拉斯矩阵进行了normalization,对角线元素都为1,所以具有scaling invariance。
- 对于每一个agents都是可导的。这使得可以使用梯度下降等方法进行优化,使得问题收敛到一个较优的值。
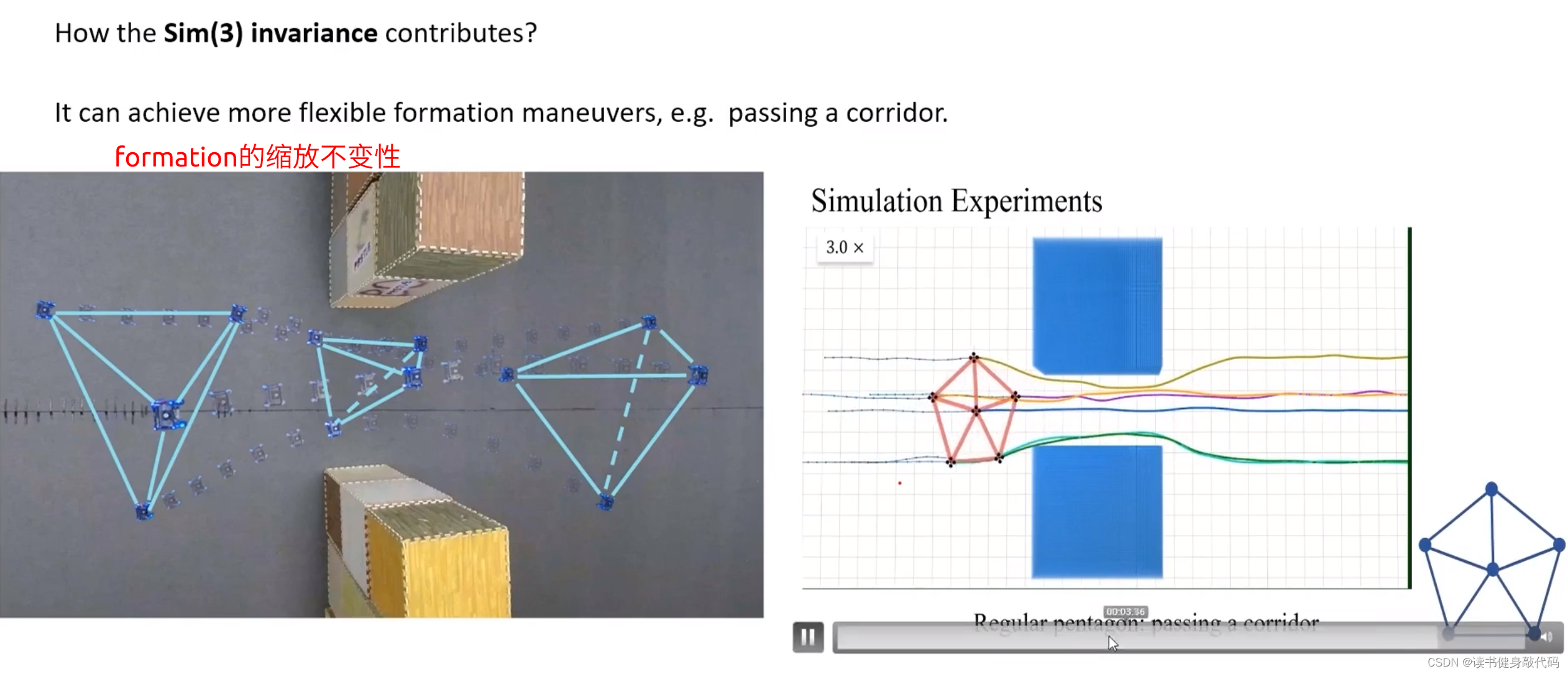
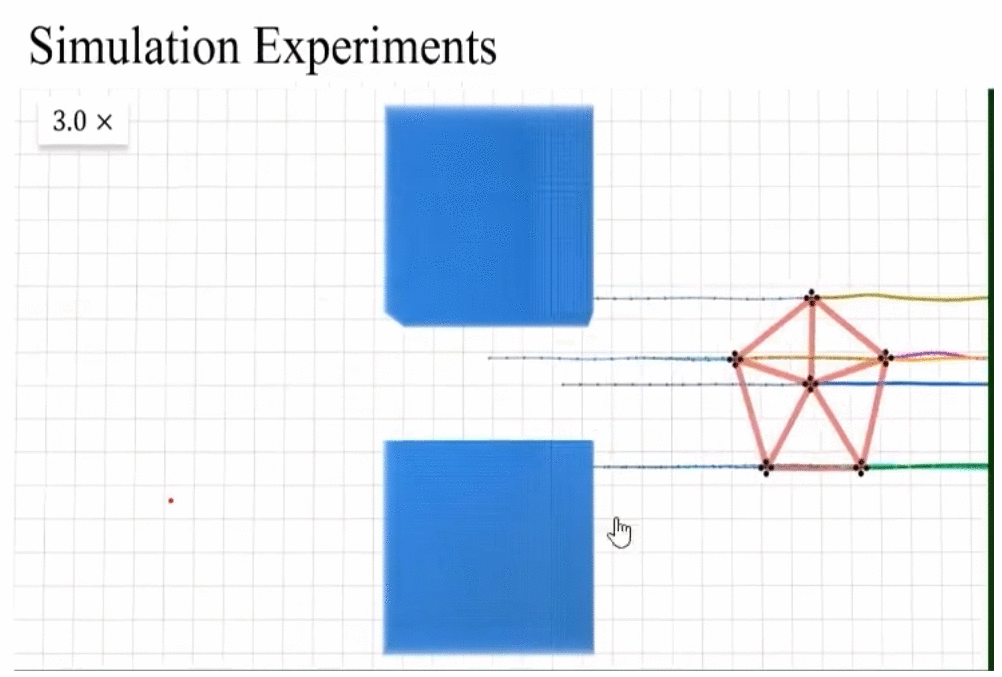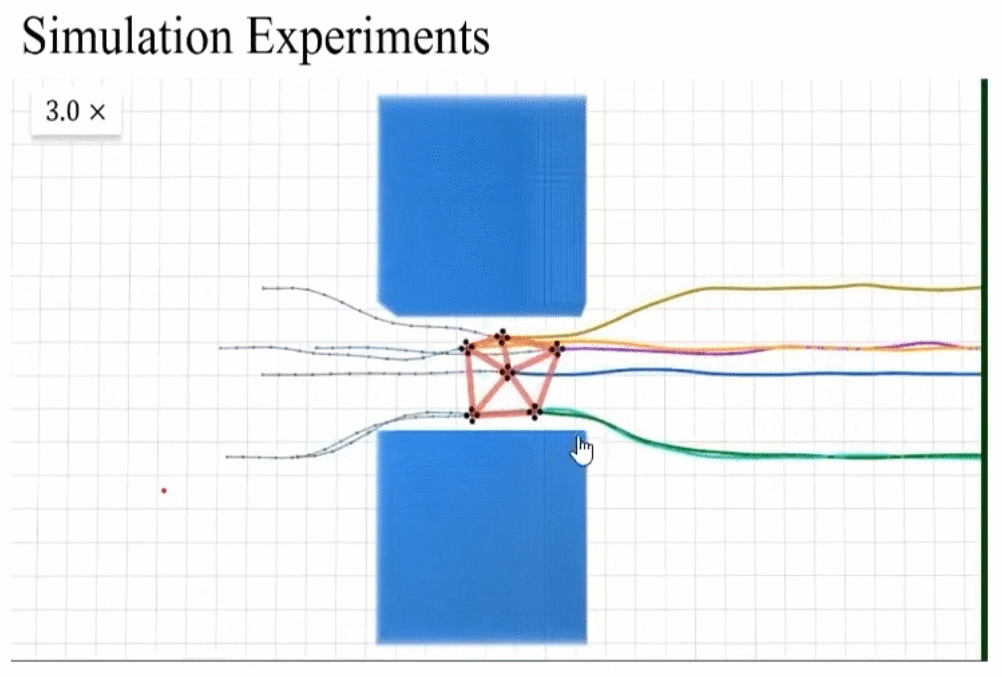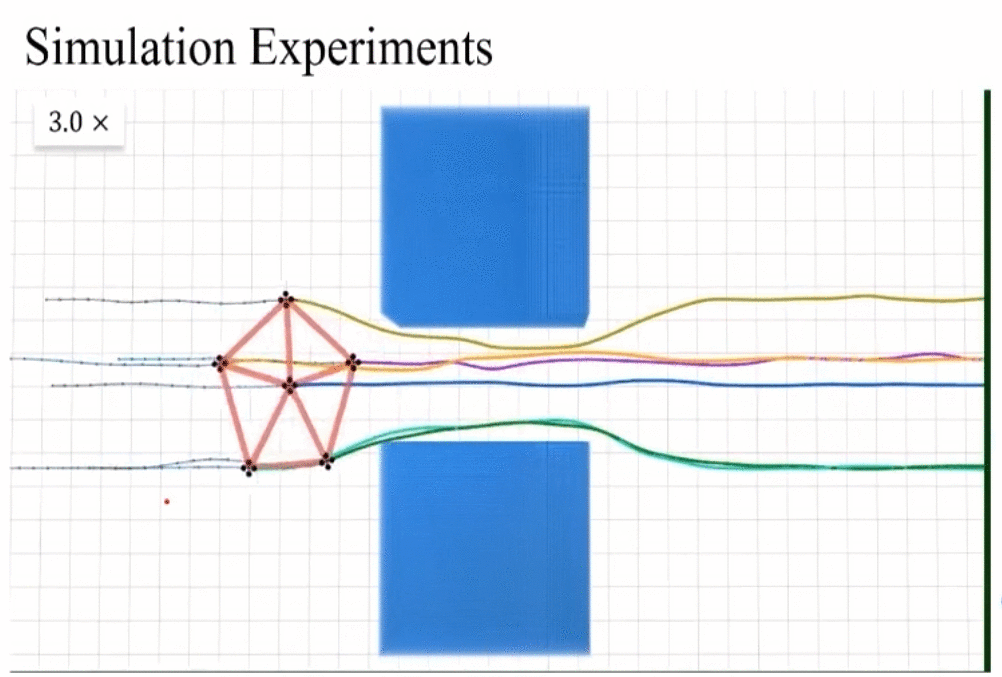
rescaling invariance实际测试和动图展示。
6. Summary
- MAPF:图搜索算法,有最优性保证,但是计算较慢,如果规模较小,可以使用图表示,则ECBS是不错的选择。
- VO:连续的算法。轻量化,常用于游戏中。但控制量是速度,对于现实中无人机,汽车等拥有自身动力学模型的对象来说不太适用,因为无法做到速度跳变。
- Flocking Model(群落模型):用于模仿群落行为,是一种rule-based的方法,缺点是如果控制某个agent,对于整个群落可能产生不可预料的影响。
- Trajectory Planning for Swarms:能够把约束等进行参数化,具有较高的自由度(ZJU Science工作在此部分,发展潜力较大)。缺点:计算量较大(如果是分布式计算,且问题复杂度确实较高,可能该方法也是个不错的选择)。
- Formation:关于集群的应用,处理多智能体系统的编队运行。(讲的比较粗略,如果有兴趣可以阅读原文)
后两个方面属于比较新的研究领域,所以讲的也比较科普化,比较粗略,如果后需要深入研究,可从后两个领域入手。
X. Reference
[1] Luna, Ryan J., and Kostas E. Bekris. “Push and swap: Fast cooperative path-finding with completeness guarantees.” Twenty-Second International Joint Conference on Artificial Intelligence. 2011.
[2] Silver, David. “Cooperative pathfinding.” Proceedings of the aaai conference on artificial intelligence and interactive digital entertainment. Vol. 1. No. 1. 2005.
[3] Standley, Trevor. “Finding optimal solutions to cooperative pathfinding problems.” Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 24. No. 1. 2010.
[4] Wagner, Glenn, and Howie Choset. “M*: A complete multirobot path planning algorithm with performance bounds.” 2011 IEEE/RSJ international conference on intelligent robots and systems. IEEE, 2011.
[5] Sharon, Guni, et al. “Conflict-based search for optimal multi-agent pathfinding.” Artificial Intelligence 219 (2015): 40-66.
[6] Röger, Gabriele, and Malte Helmert. “The more, the merrier: Combining heuristic estimators for satisficing planning.” Twentieth International Conference on Automated Planning and Scheduling. 2010.
[7] Fiorini P, Shiller Z. Motion planning in dynamic environments using velocity obstacles[J]. The International Journal of Robotics Research, 1998, 17(7): 760-772.
[8] Van den Berg J, Lin M, Manocha D. Reciprocal velocity obstacles for real-time multi-agent navigation[C]. 2008 IEEE International Conference on Robotics and Automation. IEEE, 2008: 1928-1935.
[9] Van Den Berg J, Guy S J, Lin M, et al. Reciprocal n-body collision avoidance[M]. Robotics research. Springer, Berlin, Heidelberg, 2011: 3-19.
[10] Vásárhelyi, Gábor, et al. “Optimized flocking of autonomous drones in confined environments.” Science Robotics 3.20 (2018): eaat3536.
[11] Hönig, Wolfgang, et al. “Trajectory planning for quadrotor swarms.” IEEE Transactions on Robotics 34.4 (2018): 856-869.
[12] Tordesillas, Jesus, and Jonathan P. How. “MADER: Trajectory planner in multiagent and dynamic environments.” IEEE Transactions on Robotics (2021).
[13] Liu, Sikang, Kartik Mohta, Nikolay Atanasov, and Vijay Kumar. “Towards search-based motion planning for micro aerial vehicles.” arXiv preprint arXiv:1810.03071 (2018).
[14] Olfati-Saber, R., & Murray, R. M. (2004). Consensus problems in networks of agents with switching topology and timedelays. IEEE Transactions on Automatic Control, 49(9), 1520–1533.
[15] Krick, L., Broucke, M. E., & Francis, B. A. (2008). Stabilization of infinitesimally rigid formations of multi-robot networks. In Proceedings of the 47th IEEE conference on decision and control (pp. 477–482).
[16] Zhou, X., Wen, X., Wang, Z., Gao, Y., Li, H., Wang, Q., Yang, T., Lu, H., Cao, Y., Xu, C., & Gao, F. (2022). Swarm of micro flying robots in the wild. Science Robotics, 7.
[17] D. Zhou, Z. Wang, and M. Schwager, “Agile coordination and assistive collision avoidance for quadrotor swarms using virtual structures, ”IEEE Transactions on Robotics, vol. 34, no. 4, pp. 916–923, 2018.
[18] M. Turpin, N. Michael, and V. Kumar, “Trajectory design and control for aggressive formation
flight with quadrotors,” Autonomous Robots, vol. 33, no. 1, pp. 143–156, 2012.
[19] J. Alonso-Mora, M. Schwager, and D. Rus, “Distributedmulti-robot formation control among obstacles:
A geometric and optimization approach with consensus,” in 2016 ICRA, 2016, pp.5356–5363.
[20] Quan, L., Yin, L., Xu, C., & Gao, F. (2021). Distributed Swarm Trajectory Optimization for Formation Flight in Dense Environments Accepted by ICRA 2022.










)


)





