题目要求

给定两个二叉树 p 和 q 的根，编写一个函数来检查它们是否相同。 如果两个二叉树结构相同并且节点具有相同的值，则认为它们是相同的。

Example 1:

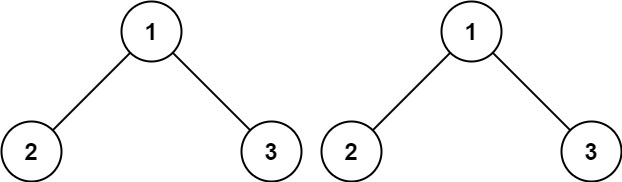
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

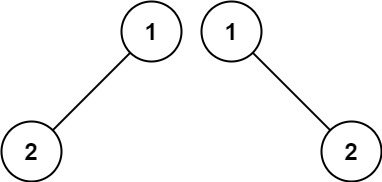
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

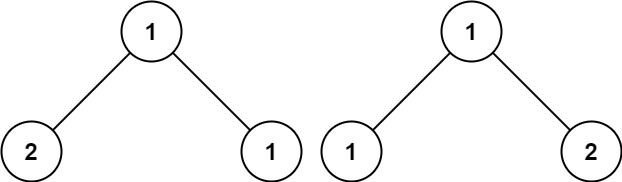
Input: p = [1,2,1], q = [1,1,2]
Output: false

思路

一道树上的操作题，定👁一看就应该用一种类似递归的算法，只不过这次是从上到下的，因为我们只要找到一个地方不同就说明两棵树不完全一样。因此我们只需要逐层判断，然后在判断左子树、右子树的情况即可。如果两棵树完全一样，则直到左右子树都为空时返回True。

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if (p == nullptr && q == nullptr) {return true;} if (p == nullptr || q == nullptr) {return false;} if (p->val != q->val) {return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);}
};

时间复杂度

基本情况分析： 当树节点（p 和 q）中的一个或两个都为 nullptr 时，就会出现基本情况。这些是恒定时间检查，因此时间复杂度为 O(1)。

递归情况分析： 函数 isSameTree 会针对两棵树中当前节点的左右子节点递归调用。在最坏的情况下，两棵树的叶子节点相同或不同。这意味着两个树中的每个节点都会被调用一次函数。

树遍历： 由于该递归函数会对每个节点精确检查一次（假设在最坏情况下，树是完整且相同的），因此时间复杂度与树中节点的数量成正比。如果每棵树中的节点总数为 n（假设两棵树的结构和节点数都相同，以进行最坏情况分析），则时间复杂度为 O(n)，其中 n 是树中的节点数。

因此，isSameTree 函数的时间复杂度为 O(n)，其中 n 是两棵树中较大的一棵树的节点数。

空间复杂度

- 在最坏的情况下，树是完全不平衡的，例如，每个节点只有一个子节点，导致递归深度为 `n`，其中 `n` 是树中的节点数。因此，调用栈（在不平衡树的情况下）造成的空间复杂度为 O(n)。
- 在最好的情况下，树是完全平衡的，树的高度为 log(n)，因此调用栈导致的最好情况下的空间复杂度为 O(log(n))。

因此，空间复杂度从平衡树的 O(log(n)) 到完全不平衡树的 O(n) 不等。