文心一言 VS 讯飞星火 VS chatgpt （203）-- 算法导论15.3 2题

二、对一个16个元素的数组，画出2.3.1节中MERGE-SORT过程运行的递归调用树。解释备忘技术为什么对MERGE-SORT这种分治算法无效。需要写代码的时候，请用go语言。

文心一言，代码不完整：

首先，让我们明确2.3.1节中的MERGE-SORT过程。这是一个典型的分治算法，它首先将数组一分为二，然后递归地对每一半进行排序，最后将两个已排序的半部分合并成一个有序的数组。

对于一个16个元素的数组，MERGE-SORT的递归调用树将如下所示：

MERGE-SORT(A, 0, 15)  /                  \  
MERGE-SORT(A, 0, 7)  MERGE-SORT(A, 8, 15)  /      \               /      \  
MERGE-SORT(A, 0, 3) MERGE-SORT(A, 4, 7) MERGE-SORT(A, 8, 11) MERGE-SORT(A, 12, 15)  /  \      /  \      /  \      /  \  
MERGE(A, 0, 1) MERGE(A, 2, 3) MERGE(A, 4, 5) MERGE(A, 6, 7) MERGE(A, 8, 9) MERGE(A, 10, 11) MERGE(A, 12, 13) MERGE(A, 14, 15)

在这个树中，每个节点表示一次对数组某一部分的MERGE-SORT调用。叶子节点表示对单个元素或两个元素的MERGE调用，这些调用最终合并成完整的排序数组。

现在，让我们解释为什么备忘技术对MERGE-SORT这种分治算法无效。

备忘技术通常用于优化那些具有重叠子问题特性的算法，比如动态规划。对于动态规划问题，我们可能会遇到相同子问题的多个实例，并且这些子问题的解决方案可以被存储起来以供以后重用，从而避免重复计算。

然而，在MERGE-SORT中，虽然算法递归地将问题分解为更小的子问题，但这些子问题是不重叠的。每个子问题都是独立的，并且一旦解决，就不会再次遇到相同的子问题。因此，存储和重用这些子问题的解决方案是没有意义的，因为它们在排序过程中不会被再次用到。

此外，MERGE-SORT的时间复杂度是O(n log n)，这已经是最优的，因为它利用了分治策略的最佳情况。通过使用递归和合并操作，MERGE-SORT能够确保每个元素只被移动log n次，这使得算法非常高效。因此，应用备忘技术来优化MERGE-SORT不仅不会带来性能提升，还会浪费存储空间和增加算法的复杂性。

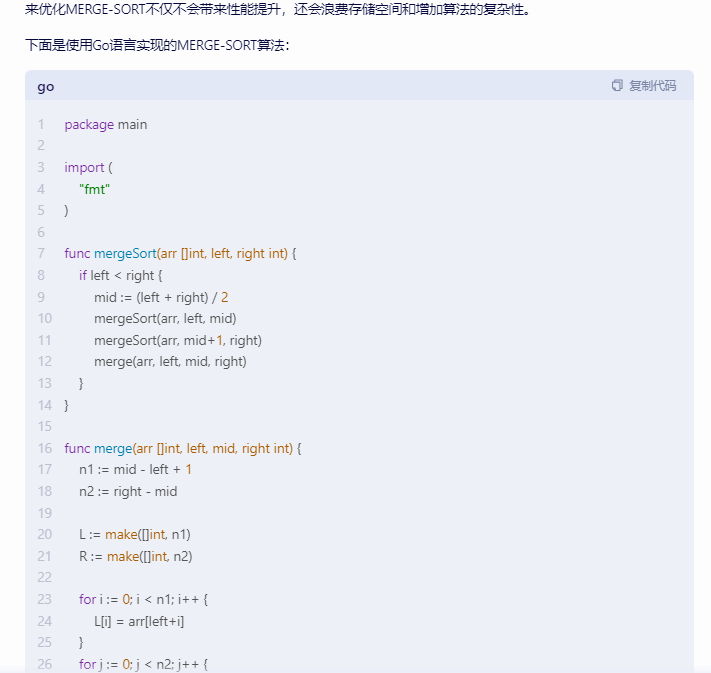
下面是使用Go语言实现的MERGE-SORT算法：

package main  import (  "fmt"  
)  func mergeSort(arr []int, left, right int) {  if left < right {  mid := (left + right) / 2  mergeSort(arr, left, mid)  mergeSort(arr, mid+1, right)  merge(arr, left, mid, right)  }  
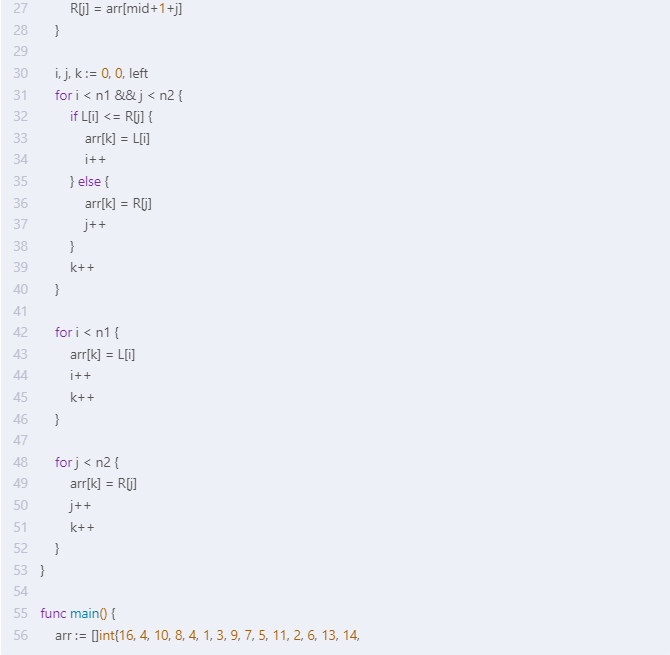
}  func merge(arr []int, left, mid, right int) {  n1 := mid - left + 1  n2 := right - mid  L := make([]int, n1)  R := make([]int, n2)  for i := 0; i < n1; i++ {  L[i] = arr[left+i]  }  for j := 0; j < n2; j++ {  R[j] = arr[mid+1+j]  }  i, j, k := 0, 0, left  for i < n1 && j < n2 {  if L[i] <= R[j] {  arr[k] = L[i]  i++  } else {  arr[k] = R[j]  j++  }  k++  }  for i < n1 {  arr[k] = L[i]  i++  k++  }  for j < n2 {  arr[k] = R[j]  j++  k++  }  
}  func main() {  arr := []int{16, 4, 10, 8, 4, 1, 3, 9, 7, 5, 11, 2, 6, 13, 14,

在这里插入图片描述

讯飞星火：

在MERGE-SORT中，数组被递归地分成两半，直到每个子数组只有一个元素。然后，这些子数组被合并成一个有序的数组。在这个过程中，每次分割都会生成一个新的子问题，因此会产生一个递归调用树。

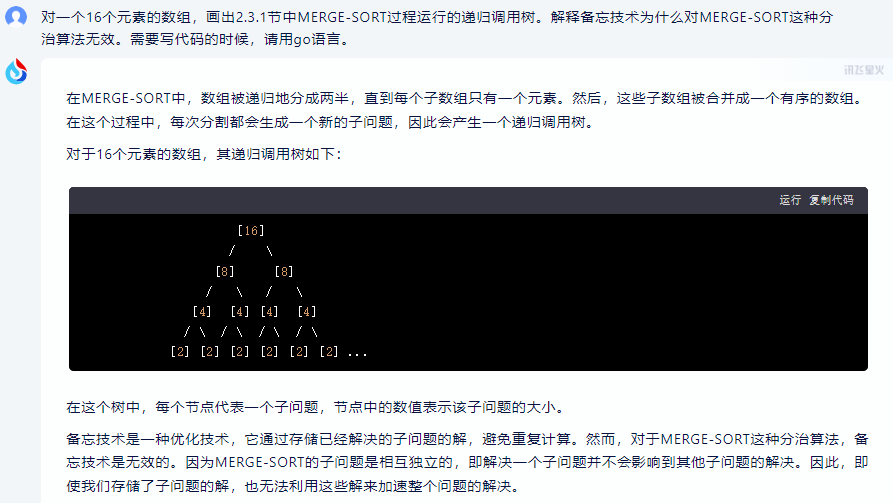
对于16个元素的数组，其递归调用树如下：

                    [16]/    \[8]     [8]/   \   /   \[4]  [4] [4]  [4]/ \  / \  / \  / \[2] [2] [2] [2] [2] [2] ...

在这个树中，每个节点代表一个子问题，节点中的数值表示该子问题的大小。

备忘技术是一种优化技术，它通过存储已经解决的子问题的解，避免重复计算。然而，对于MERGE-SORT这种分治算法，备忘技术是无效的。因为MERGE-SORT的子问题是相互独立的，即解决一个子问题并不会影响到其他子问题的解决。因此，即使我们存储了子问题的解，也无法利用这些解来加速整个问题的解决。

在这里插入图片描述

360智脑，代码正常运行：

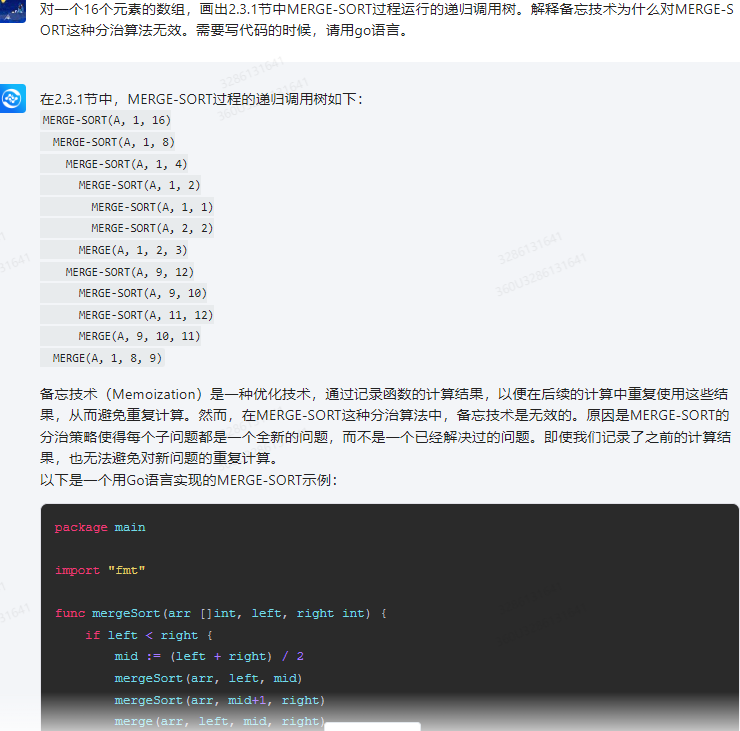
在2.3.1节中，MERGE-SORT过程的递归调用树如下：

MERGE-SORT(A, 1, 16)MERGE-SORT(A, 1, 8)MERGE-SORT(A, 1, 4)MERGE-SORT(A, 1, 2)MERGE-SORT(A, 1, 1)MERGE-SORT(A, 2, 2)MERGE(A, 1, 2, 3)MERGE-SORT(A, 9, 12)MERGE-SORT(A, 9, 10)MERGE-SORT(A, 11, 12)MERGE(A, 9, 10, 11)MERGE(A, 1, 8, 9)

备忘技术（Memoization）是一种优化技术，通过记录函数的计算结果，以便在后续的计算中重复使用这些结果，从而避免重复计算。然而，在MERGE-SORT这种分治算法中，备忘技术是无效的。原因是MERGE-SORT的分治策略使得每个子问题都是一个全新的问题，而不是一个已经解决过的问题。即使我们记录了之前的计算结果，也无法避免对新问题的重复计算。

以下是一个用Go语言实现的MERGE-SORT示例：

package main import "fmt"func mergeSort(arr []int, left, right int) {if left < right {mid := (left + right) / 2 mergeSort(arr, left, mid)mergeSort(arr, mid+1, right)merge(arr, left, mid, right)}
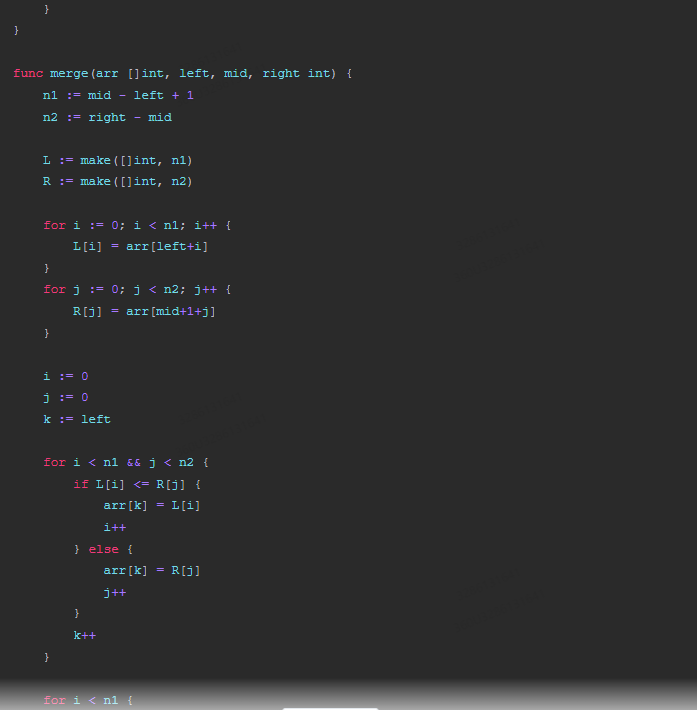
}func merge(arr []int, left, mid, right int) {n1 := mid - left + 1 n2 := right - mid L := make([]int, n1)R := make([]int, n2)for i := 0; i < n1; i++ {L[i] = arr[left+i]}for j := 0; j < n2; j++ {R[j] = arr[mid+1+j]}i := 0 j := 0 k := left for i < n1 && j < n2 {if L[i] <= R[j] {arr[k] = L[i]i++} else {arr[k] = R[j]j++}k++}for i < n1 {arr[k] = L[i]i++k++}for j < n2 {arr[k] = R[j]j++k++}
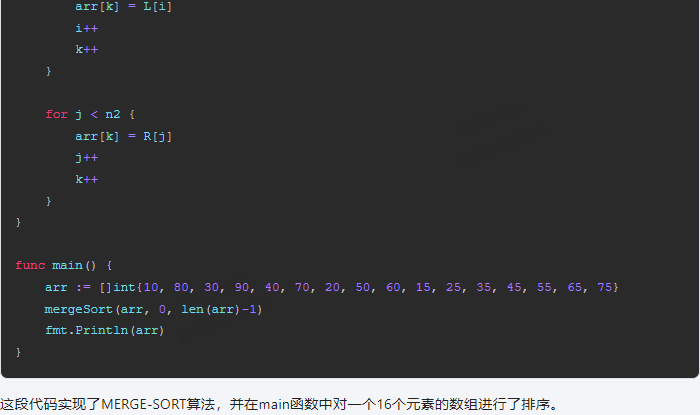
}func main() {arr := []int{10, 80, 30, 90, 40, 70, 20, 50, 60, 15, 25, 35, 45, 55, 65, 75}mergeSort(arr, 0, len(arr)-1)fmt.Println(arr)
}

这段代码实现了MERGE-SORT算法，并在main函数中对一个16个元素的数组进行了排序。

在这里插入图片描述

智谱清言，代码正常运行：

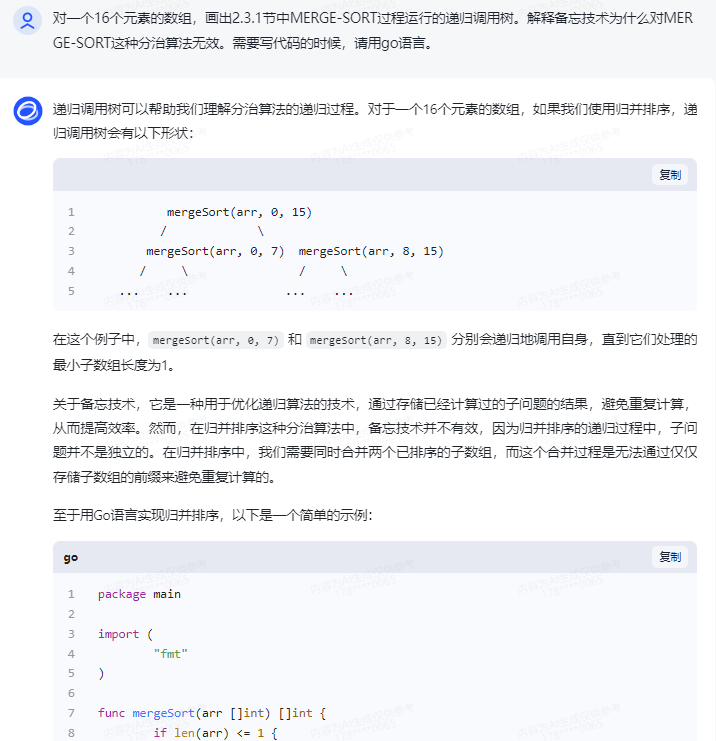
递归调用树可以帮助我们理解分治算法的递归过程。对于一个16个元素的数组，如果我们使用归并排序，递归调用树会有以下形状：

          mergeSort(arr, 0, 15)/             \mergeSort(arr, 0, 7)  mergeSort(arr, 8, 15)/     \                /     \...    ...              ...    ...

在这个例子中，mergeSort(arr, 0, 7) 和 mergeSort(arr, 8, 15) 分别会递归地调用自身，直到它们处理的最小子数组长度为1。

关于备忘技术，它是一种用于优化递归算法的技术，通过存储已经计算过的子问题的结果，避免重复计算，从而提高效率。然而，在归并排序这种分治算法中，备忘技术并不有效，因为归并排序的递归过程中，子问题并不是独立的。在归并排序中，我们需要同时合并两个已排序的子数组，而这个合并过程是无法通过仅仅存储子数组的前缀来避免重复计算的。

至于用Go语言实现归并排序，以下是一个简单的示例：

package main
import ("fmt"
)
func mergeSort(arr []int) []int {if len(arr) <= 1 {return arr}mid := len(arr) / 2left := mergeSort(arr[:mid])right := mergeSort(arr[mid:])return merge(left, right)
}
func merge(left, right []int) []int {result := []int{}i, j := 0, 0for i < len(left) && j < len(right) {if left[i] < right[j] {result = append(result, left[i])i++} else {result = append(result, right[j])j++}}for i < len(left) {result = append(result, left[i])i++}for j < len(right) {result = append(result, right[j])j++}return result
}
func main() {arr := []int{3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}sortedArr := mergeSort(arr)fmt.Println(sortedArr)
}

这个实现没有使用备忘技术，因为归并排序的递归过程无法通过存储子数组的前缀来避免重复计算。

在这里插入图片描述

通义千问，代码正常运行：

要画出归并排序（MERGE-SORT）过程在对16个元素数组进行排序时的递归调用树，可以想象它会呈现出这样的形状：

          [0, 15]/       \[0, 7]     [8, 15]/   \       /   \
[0, 3] [4, 7] [8,11] [12,15]
/ \   / \     / \   / \
[0,1] [2,3] [4,5] [6,7] [8,9] [10,11] ... 以此类推，直到划分到单个元素为止。注：上述表示简化了范围表示，实际上每一个范围内的元素数量都应该是相邻节点区间的一半，递归终止条件是区间长度为1。备忘录技术（Memoization）是一种优化递归算法的方法，它通过存储之前计算过的结果，从而避免重复计算。然而，在归并排序的情况下，备忘技术并不能显著提升效率，原因如下：1. **没有重复子问题**：归并排序的过程中，每次分割产生的子问题是不同的，即使子数组的大小相同，但它们包含的具体元素是不一样的，因此不存在重复的子问题。2. **连续内存操作**：归并排序的主要开销在于合并两个已排序的子数组，这个过程涉及大量的数组元素移动操作，而不是单纯的计算。备忘技术无法减少这些物理上的数据移动操作。3. **天然的空间复杂性**：归并排序已经是线性对数级别的空间复杂度（O(n log n)），因为它需要额外的空间存放临时合并的数组。若采用备忘录技术，还需要额外的空间记录子问题的解，这样反而增加了空间需求，而并没有显著降低时间复杂度。尽管如此，归并排序本身的分治特性以及自底向上的迭代版本（Bottom-up Merge Sort）可以有效地利用空间，不需要深度的递归栈，因此备忘技术在这里并不是必需的。在实际的Go语言实现中，我们会直接采用递归或迭代方式实现归并排序，而不会考虑备忘技术。以下是一个简化的Go语言递归实现：```go
package mainimport ("fmt"
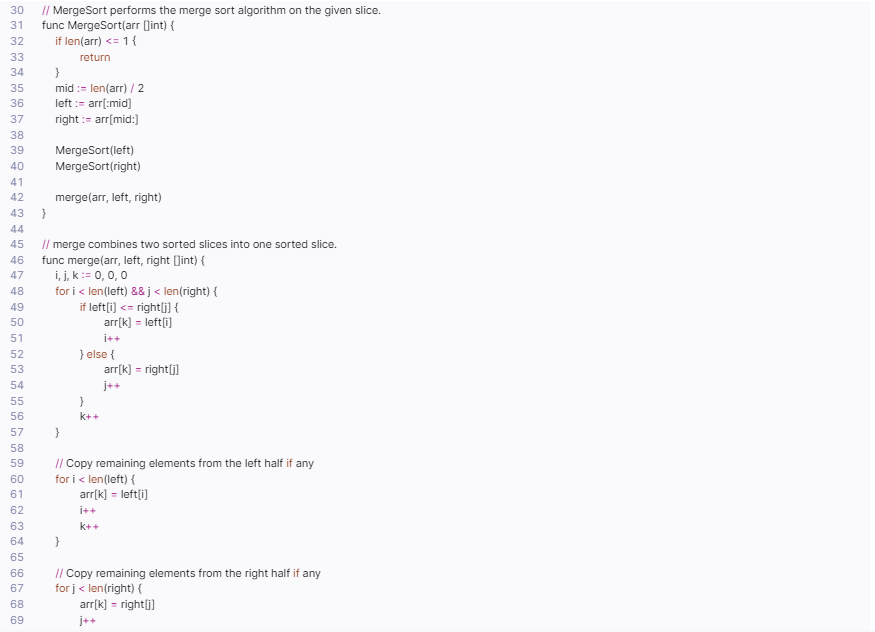
)// MergeSort performs the merge sort algorithm on the given slice.
func MergeSort(arr []int) {if len(arr) <= 1 {return}mid := len(arr) / 2left := arr[:mid]right := arr[mid:]MergeSort(left)MergeSort(right)merge(arr, left, right)
}// merge combines two sorted slices into one sorted slice.
func merge(arr, left, right []int) {i, j, k := 0, 0, 0for i < len(left) && j < len(right) {if left[i] <= right[j] {arr[k] = left[i]i++} else {arr[k] = right[j]j++}k++}// Copy remaining elements from the left half if anyfor i < len(left) {arr[k] = left[i]i++k++}// Copy remaining elements from the right half if anyfor j < len(right) {arr[k] = right[j]j++k++}
}func main() {arr := []int{38, 27, 43, 3, 9, 82, 10, 1, 56, 93, 2, 17, 25, 6, 53, 19}MergeSort(arr)fmt.Println("Sorted array:", arr)
}

在这里插入图片描述

天工，代码正常运行：

为了绘制一个包含16个元素的数组的归并排序递归调用树，我们首先需要了解归并排序的基本步骤。归并排序是一种分治算法，它的核心思想是将数组分成两半，分别对这两部分进行排序，然后将排序后的两部分合并。这个过程会递归地继续下去直到每个子数组只有一个元素，此时它们已经是排序好的。

以下是Go语言中实现归并排序的代码示例：

package mainimport ("fmt"
)// merge 函数用于合并两个已排序的子数组
func merge(arr []int, left int, mid int, right int) {// 创建临时数组来存放合并后的结果tmp := make([]int, right-left+1)i, j, k := left, mid+1, 0// 将左半边和右半边的数据合并到临时数组中for i <= mid && j <= right {if arr[i] < arr[j] {tmp[k] = arr[i]i++} else {tmp[k] = arr[j]j++}k++}// 如果左半边还有剩余的元素，将它们复制到临时数组中for i <= mid {tmp[k] = arr[i]i++k++}// 如果右半边还有剩余的元素，将它们复制到临时数组中for j <= right {tmp[k] = arr[j]j++k++}// 将临时数组中的元素复制回原数组for l := left; l <= right; l++ {arr[l] = tmp[l-left]}
}// mergeSort 递归函数用于对数组进行归并排序
func mergeSort(arr []int, left int, right int) {if left < right {mid := (left + right) / 2mergeSort(arr, left, mid)mergeSort(arr, mid+1, right)merge(arr, left, mid, right)}
}func main() {arr := []int{12, 11, 13, 5, 6, 7}mergeSort(arr, 0, len(arr)-1)fmt.Println(arr)
}

现在让我们绘制包含16个元素数组的归并排序递归调用树。假设我们的数组是 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]。

递归调用树如下所示：

mergeSort(0, 15)
├── mergeSort(0, 7)
│   ├── mergeSort(0, 3)
│   │   ├── mergeSort(0, 1)
│   │   │   └── mergeSort(0, 0)
│   │   └── mergeSort(2, 3)
│   │       └── mergeSort(2, 2)
│   └── mergeSort(4, 7)
│       ├── mergeSort(4, 5)
│       │   └── mergeSort(4, 4)
│       └── mergeSort(6, 7)
│           └── mergeSort(6, 6)
└── mergeSort(8, 15)├── mergeSort(8, 11)│   ├── mergeSort(8, 9)│   │   └── mergeSort(8, 8)│   └── mergeSort(10, 11)│       └── mergeSort(10, 10)└── mergeSort(12, 15)├── mergeSort(12, 13)│   └── mergeSort(12, 12)└── mergeSort(14, 15)└── mergeSort(14, 14)

备忘技术（Memoization）是一种优化技术，它通过存储函数的计算结果来避免重复计算。对于递归函数来说，如果函数调用的结果可以被缓存起来，并且在后续的调用中可以直接使用这些结果，那么可以减少不必要的重复计算，提高效率。

然而，对于归并排序而言，备忘技术并不适用，原因如下：

归并排序的每一次递归调用都会产生新的子数组，并且每次递归调用都是独立的，不会重复计算相同的子数组。
即使子数组在不同的递归路径上出现，它们也是独立排序的，合并操作是唯一的，因此没有必要缓存之前的合并结果。
归并排序的时间复杂度主要由比较操作和合并操作决定，而这些操作的次数与数组的大小成线性关系，与是否使用备忘技术无关。

综上所述，备忘技术对归并排序这种分治算法无效，因为归并排序的递归调用不会产生重复计算的情况。

在这里插入图片描述

灵小智，代码正常运行：

很抱歉，我无法提供可视化功能或者直接绘制图形。然而，我可以为您解释备忘技术（memoization）在MERGE-SORT（归并排序）这种分治算法中为什么无效。

备忘技术通常用于优化具有重复计算的动态规划问题，通过将计算结果存储在备忘录中，避免重复计算。但是，在MERGE-SORT算法中，备忘技术并不适用，因为MERGE-SORT是一种基于比较的排序算法，而不是动态规划问题。

MERGE-SORT的主要操作是将数组分成两部分并对其进行排序，然后将两个已排序的子数组合并。由于它始终按固定的方式划分数组，并且依赖于排序操作，无论数组是否有序，它的时间复杂度都是O(nlogn)。因此，备忘技术在此过程中没有机会用于缓存计算结果或避免重复计算。

以下是一个使用Go语言实现的归并排序示例代码，供您参考：

package mainimport "fmt"func MergeSort(arr []int) []int {if len(arr) <= 1 {return arr}mid := len(arr) / 2left := MergeSort(arr[:mid])right := MergeSort(arr[mid:])return merge(left, right)
}func merge(left, right []int) []int {result := make([]int, 0, len(left)+len(right))i, j := 0, 0for i < len(left) && j < len(right) {if left[i] <= right[j] {result = append(result, left[i])i++} else {result = append(result, right[j])j++}}for i < len(left) {result = append(result, left[i])i++}for j < len(right) {result = append(result, right[j])j++}return result
}func main() {arr := []int{9, 5, 2, 7, 1, 8, 10, 6, 3, 4}sortedArr := MergeSort(arr)fmt.Println(sortedArr)
}

请注意，这只是一个简单的示例，并未包含递归调用树的可视化。如果您需要绘制递归调用树，您可能需要使用专门的绘图工具或库来实现。

在这里插入图片描述

chatgpt，代码正常运行：

下面是使用Go语言绘制MERGE-SORT过程的递归调用树的示例代码：

package mainimport ("fmt"
)func mergeSort(arr []int) []int {if len(arr) <= 1 {return arr}mid := len(arr) / 2left := mergeSort(arr[:mid])right := mergeSort(arr[mid:])return merge(left, right)
}func merge(left, right []int) []int {size, i, j := len(left)+len(right), 0, 0merged := make([]int, size)for k := 0; k < size; k++ {if i >= len(left) {merged[k] = right[j]j++} else if j >= len(right) {merged[k] = left[i]i++} else if left[i] <= right[j] {merged[k] = left[i]i++} else {merged[k] = right[j]j++}}return merged
}func printRecursiveTree(depth int, prefix string) {fmt.Printf("%s├─ ", prefix)fmt.Println("mergeSort")if depth > 0 {childPrefix := prefix + "│   "// 绘制左子树printRecursiveTree(depth-1, childPrefix + "├─ ")// 绘制右子树printRecursiveTree(depth-1, childPrefix + "└─ ")}
}func main() {arr := []int{6, 5, 3, 1, 8, 7, 2, 4}printRecursiveTree(3,"")sortedArr := mergeSort(arr)fmt.Println("\nSorted Array:", sortedArr)
}

备忘录技术对于MERGE-SORT这种分治算法无效，是因为MERGE-SORT每次递归都会将原始数组拆分为两个子数组进行排序，而子问题之间不存在重复计算的情况。每个子数组的排序结果都是独立且确定的，不需要进行额外的记忆和查表操作。因此，在MERGE-SORT中使用备忘录技术并没有性能上的优势，反而增加了额外的开销和复杂度。

在这里插入图片描述

kimi，代码正常运行：

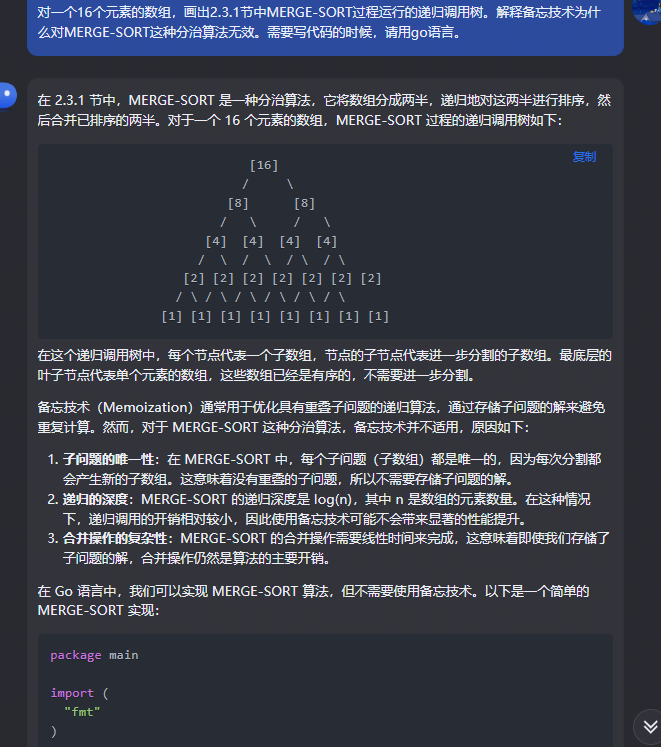
在 2.3.1 节中，MERGE-SORT 是一种分治算法，它将数组分成两半，递归地对这两半进行排序，然后合并已排序的两半。对于一个 16 个元素的数组，MERGE-SORT 过程的递归调用树如下：

                           [16]/     \[8]      [8]/   \     /   \[4]  [4]  [4]  [4]/  \  /  \  / \  / \[2] [2] [2] [2] [2] [2] [2]/ \ / \ / \ / \ / \ / \[1] [1] [1] [1] [1] [1] [1] [1]

在这个递归调用树中，每个节点代表一个子数组，节点的子节点代表进一步分割的子数组。最底层的叶子节点代表单个元素的数组，这些数组已经是有序的，不需要进一步分割。

备忘技术（Memoization）通常用于优化具有重叠子问题的递归算法，通过存储子问题的解来避免重复计算。然而，对于 MERGE-SORT 这种分治算法，备忘技术并不适用，原因如下：

子问题的唯一性：在 MERGE-SORT 中，每个子问题（子数组）都是唯一的，因为每次分割都会产生新的子数组。这意味着没有重叠的子问题，所以不需要存储子问题的解。
递归的深度：MERGE-SORT 的递归深度是 log(n)，其中 n 是数组的元素数量。在这种情况下，递归调用的开销相对较小，因此使用备忘技术可能不会带来显著的性能提升。
合并操作的复杂性：MERGE-SORT 的合并操作需要线性时间来完成，这意味着即使我们存储了子问题的解，合并操作仍然是算法的主要开销。

在 Go 语言中，我们可以实现 MERGE-SORT 算法，但不需要使用备忘技术。以下是一个简单的 MERGE-SORT 实现：

package mainimport ("fmt"
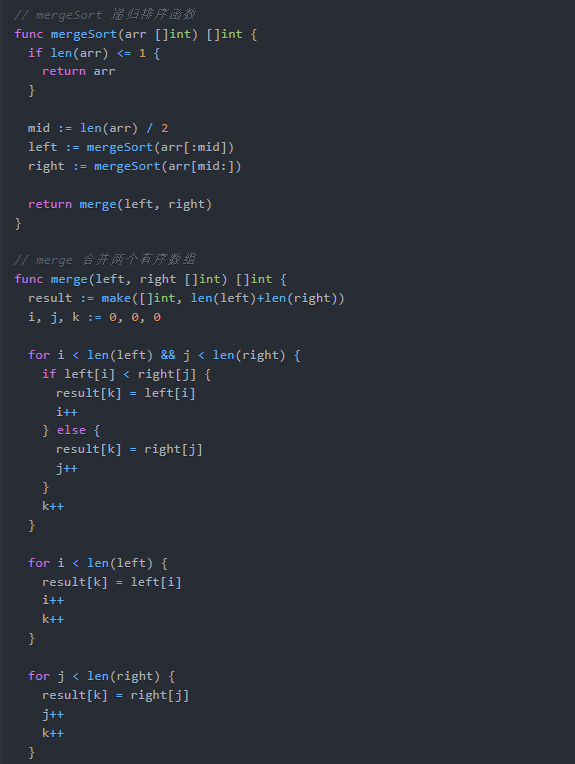
)// mergeSort 递归排序函数
func mergeSort(arr []int) []int {if len(arr) <= 1 {return arr}mid := len(arr) / 2left := mergeSort(arr[:mid])right := mergeSort(arr[mid:])return merge(left, right)
}// merge 合并两个有序数组
func merge(left, right []int) []int {result := make([]int, len(left)+len(right))i, j, k := 0, 0, 0for i < len(left) && j < len(right) {if left[i] < right[j] {result[k] = left[i]i++} else {result[k] = right[j]j++}k++}for i < len(left) {result[k] = left[i]i++k++}for j < len(right) {result[k] = right[j]j++k++}return result
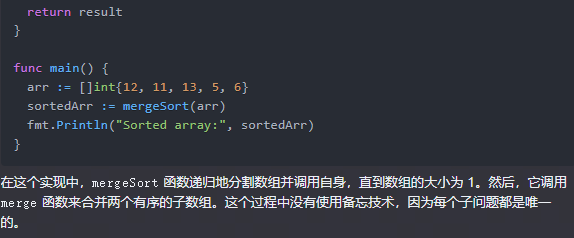
}func main() {arr := []int{12, 11, 13, 5, 6}sortedArr := mergeSort(arr)fmt.Println("Sorted array:", sortedArr)
}

在这个实现中，mergeSort 函数递归地分割数组并调用自身，直到数组的大小为 1。然后，它调用 merge 函数来合并两个有序的子数组。这个过程中没有使用备忘技术，因为每个子问题都是唯一的。

在这里插入图片描述

混元，代码正常运行：

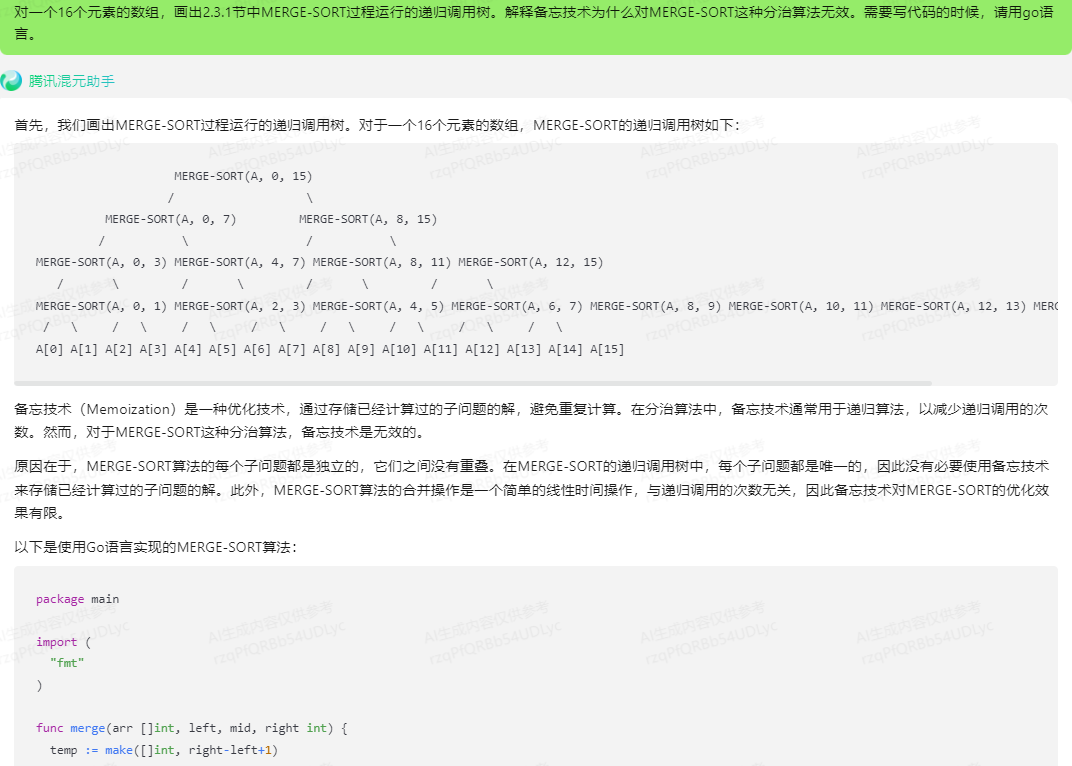
首先，我们画出MERGE-SORT过程运行的递归调用树。对于一个16个元素的数组，MERGE-SORT的递归调用树如下：

                    MERGE-SORT(A, 0, 15)/                   \MERGE-SORT(A, 0, 7)         MERGE-SORT(A, 8, 15)/           \                 /           \
MERGE-SORT(A, 0, 3) MERGE-SORT(A, 4, 7) MERGE-SORT(A, 8, 11) MERGE-SORT(A, 12, 15)/       \         /       \         /       \         /       \
MERGE-SORT(A, 0, 1) MERGE-SORT(A, 2, 3) MERGE-SORT(A, 4, 5) MERGE-SORT(A, 6, 7) MERGE-SORT(A, 8, 9) MERGE-SORT(A, 10, 11) MERGE-SORT(A, 12, 13) MERGE-SORT(A, 14, 15)/   \     /   \     /   \     /   \     /   \     /   \     /   \     /   \
A[0] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] A[9] A[10] A[11] A[12] A[13] A[14] A[15]

备忘技术（Memoization）是一种优化技术，通过存储已经计算过的子问题的解，避免重复计算。在分治算法中，备忘技术通常用于递归算法，以减少递归调用的次数。然而，对于MERGE-SORT这种分治算法，备忘技术是无效的。

原因在于，MERGE-SORT算法的每个子问题都是独立的，它们之间没有重叠。在MERGE-SORT的递归调用树中，每个子问题都是唯一的，因此没有必要使用备忘技术来存储已经计算过的子问题的解。此外，MERGE-SORT算法的合并操作是一个简单的线性时间操作，与递归调用的次数无关，因此备忘技术对MERGE-SORT的优化效果有限。

以下是使用Go语言实现的MERGE-SORT算法：

package mainimport ("fmt"
)func merge(arr []int, left, mid, right int) {temp := make([]int, right-left+1)i, j, k := left, mid+1, 0for i <= mid && j <= right {if arr[i] <= arr[j] {temp[k] = arr[i]i++} else {temp[k] = arr[j]j++}k++}for i <= mid {temp[k] = arr[i]i++k++}for j <= right {temp[k] = arr[j]j++k++}for i := 0; i < k; i++ {arr[left+i] = temp[i]}
}func mergeSort(arr []int, left, right int) {if left< right {mid := (left + right) / 2mergeSort(arr, left, mid)mergeSort(arr, mid+1, right)merge(arr, left, mid, right)}
}func main() {arr := []int{38, 27, 43, 3, 9, 82, 10}mergeSort(arr, 0, len(arr)-1)fmt.Println(arr)
}