- 难度: 中等
- 通过率: 37.6%
- 题目链接:. - 力扣(LeetCode)
题目描述
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[[2],[3,4],[6,5,7],[4,1,8,3] ]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
解法一:递归
从第一层起,在某一层上,希望知道顶点到该层上的最短的路径为多少。这需要在该层上,计算顶点到达每个点的路径和,然后取最小的。到某个点的最短路径,即用该点的值加上到达该点上方两个点的最短路径。由此分析,这可以写成一个递归调用。
min_path_sum 计算到达地 level 层的第 i 个点的最短路径和。首先从最后一层的每个点出发,递归地调用 min_path_sum,求出达到该点上一层左右两个节点的最短路径,进而得到到达该点的最短路径。
class Solution {
public:int minimumTotal(vector<vector<int>>& triangle) {int min_total = INT_MAX;int level = triangle.size() - 1;for(int i = 0; i < triangle[level].size(); i++){int n = min_path_sum(triangle, level, i);min_total = min(min_total, n);}return min_total;}int min_path_sum(vector<vector<int>>& triangle, int level, int i){if(level == 0){return triangle[0][0];}int n1 = INT_MAX, n2 = INT_MAX;if(i < triangle[level-1].size()){n1 = min_path_sum(triangle, level-1, i);}if(i > 0){n2 = min_path_sum(triangle, level-1, i-1);}return min(n1, n2) + triangle[level][i];}
};
上面这算法是正确的,但是不能性能太差,因为存在大量的重复计算。可以采用备忘录,避免重复计算。但是此问题还有更简洁的解法,见解法二。
解法二:
2
3 4
6 5 7
4 1 8 3
输入的三角形,可以视为一个栅栏网络,遇到栅栏网络,我首先想到了维特比算法。三角形的每一层都看做一个栅栏,只有相邻的栅栏相互连接。如下图:
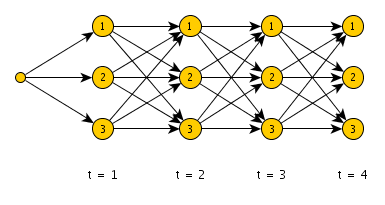
图中任何一个点,到起点的路径之和,都可以基于前一层节点到起点的路径和计算出来。比如上图中的第二层编号为 1 的点,只需要用第一层中三个点中最小值加上自身就可以了,其余点也可以这么一层层地计算出来。
本题中,我们可以从下往上计算,因为这样可以很容易确定前一层与节点 i 相连的节点(i 和 i+1)。
class Solution {
public:int minimumTotal(vector<vector<int>> &triangle) {if (triangle.size() == 1) {return triangle[0][0];}for (int level = triangle.size() - 2; level >= 0; level--) {for (int i = 0; i < triangle[level].size(); i++) {int n = min(triangle[level + 1][i], triangle[level + 1][i + 1]);triangle[level][i] += n;}}return triangle[0][0];}
};


















