超平面公式
(1) 超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中,一条直线是一维的,它把平面分成了两部分;三维空间中,一个平面是二维的,它把空间分成了两部分。(2) 法向量是指垂直于超平面的向量。
以下向量均为列向量
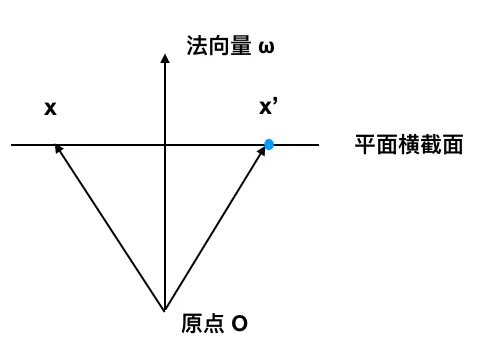
假如有法向量 ω \omega ω(垂直于超平面) ,已知超平面中的一点 x , x^, x,,对于超平面中的任意一点 x x x,均有 ω \omega ω 垂直于向量 x − x , x-x^, x−x,。公式表示就是:
ω T ( x − x , ) = 0 \omega^T(x-x^,)=0 ωT(x−x,)=0
展开有 ω T x ω T x , = 0 \omega^T x\omega^T x^,=0 ωTxωTx,=0
另 b = − ω T x , = − ( w 1 x 1 , + w 2 x 2 , + . . . + w n x n , ) b = -\omega^T x^,=-(w^1 x^,_1+w^2 x^,_2+...+w^n x^,_n) b=−ωTx,=−(w1x1,+w2x2,+...+wnxn,)
则有 ω T x + b = 0 \omega^T x+b=0 ωTx+b=0
所以超平面的公式可以写成:
ω T x + b = 0 \omega^T x+b=0 ωTx+b=0
其中 ω \omega ω 为 N 维向量,b为标量,表示超平面于原点之间的距离
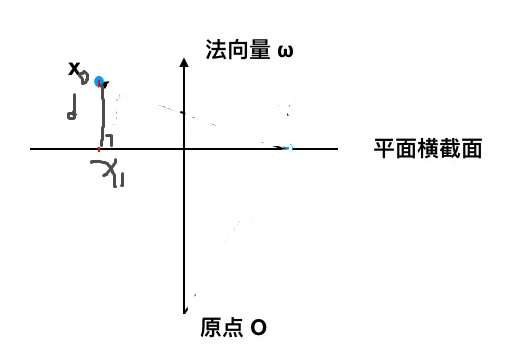
点到超平面距离
现在我们有一点 x 0 x_0 x0,需要求它到超平面之间的距离

参考:
如何理解超平面?
超平面是什么?——理解超平面(SVM开篇之超平面详解)
SVM:任意点到超平面的距离公式






springmvc+mybatis+dubbo+zookeeper分布式架构 整合 - maven构建ant-framework核心代码Base封装)






)



--高清晰度字体和窗体分辨率问题。)

