机械臂目标抓捕学习笔记【1】

基于概率量度的机械臂视觉伺服目标捕获运动规划方法

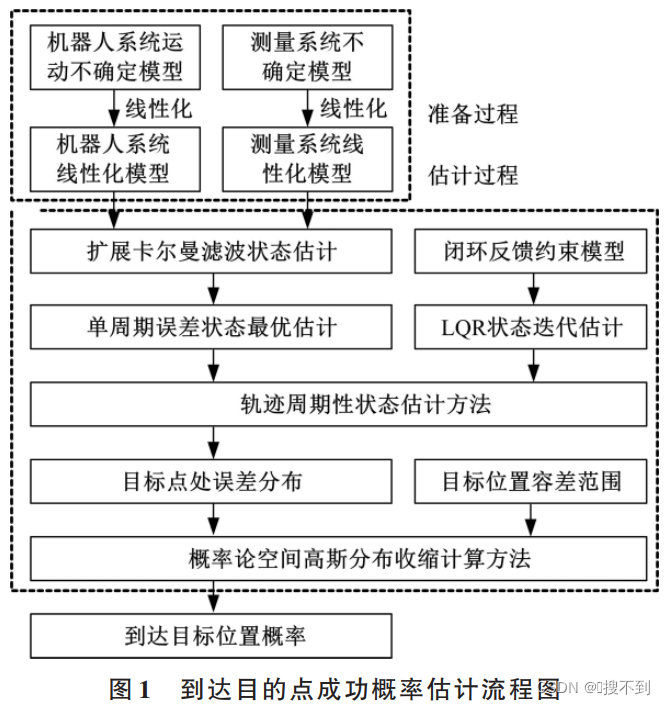
期望轨迹序列

机器人轨迹 Π序列表示为系统预定义状态、控制输入：
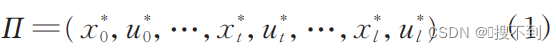
在这里插入图片描述
其中 $l$ 为整条预定义轨迹的周期数，

状态转移函数

下个周期的系统状态是当前系统状态、指令输入和运动误差的函数：
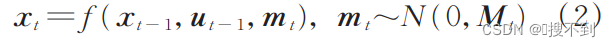
在这里插入图片描述

系统测量值

当机器人运动系统存在过程噪声，希望通过外部测量或机器人自身携带的传感器形成运动反馈时，测量值只与两个因素相关：一个是机器人系统状态；另一个是测量系统本身的观测噪声。写成函数的形式为：
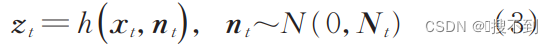
在这里插入图片描述

模型线性化

针对离散化周期系统，对模型型（2、3）利用一阶 Taylor展开。

在式（2）的预定义轨迹点（ $x_{t-1}^{*}$ , $u_{t-1}^{*}$ ）处进行线性化， $m_t$ 在0处展开，则有：
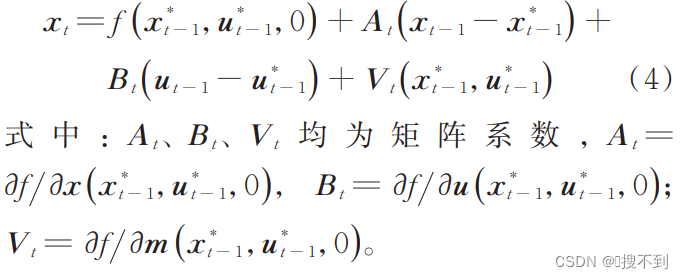
在这里插入图片描述

在式（3）的预定义轨迹点（ $x_{t}^{*}$ ）处进行线性化， $n_t$ 在0处展开，则有：
在这里插入图片描述

对上式整理可以得到：
在这里插入图片描述

卡尔曼滤波状态估计

在这里插入图片描述

代价函数-闭环反馈

闭环反馈的目的是使实际轨迹与预定义轨迹之间的偏移量最小：

线性二次型（LQR）最优解具备求解过程的规范化，可简单地采用状态线性反馈控制律构成闭环最优控制系统，兼顾系统状态和输入指标。求解过程可以表示为：
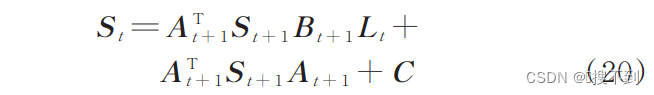
在这里插入图片描述

轨迹误差方差

结合式(8)和(17)，可得：
$u_{t}=L_{t}\tilde{x}_{t}+u_{t}^{*} \\ x_{t}= \overline{x}_{t}+x_{t}^{*}$
进一步可整理为：
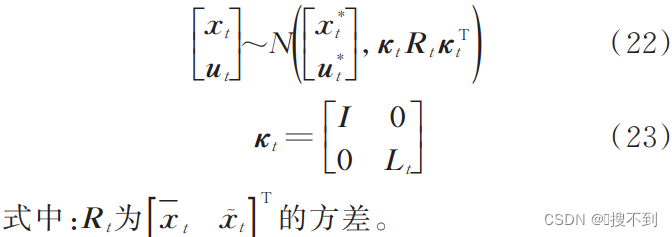
在这里插入图片描述

通过式（21）~（23）对整个轨迹过程的各中断周期内的系统状态进行估计。

将式(9、17)代入式(12)，得到：
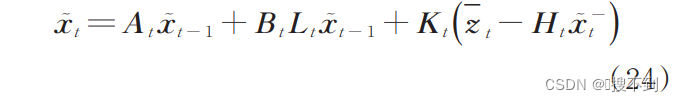
在这里插入图片描述
将式(6、7、9)代入式(24)，转化为：

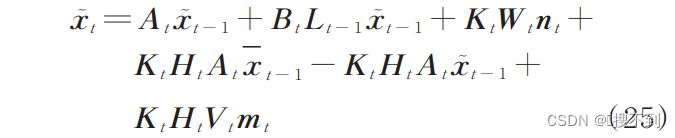
将式（17）代入式（6）得：

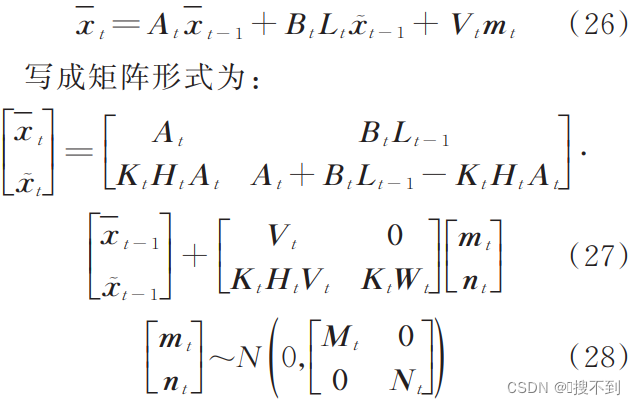
系统状态的初始方差 $R_0$ 可以设置为一个较大的初始值，这个初始值会随着系统状态估计迅速收敛到正常的估计值范围。

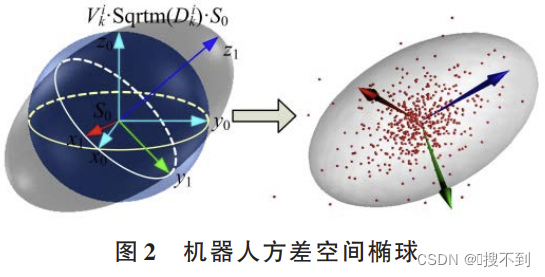
误差几何化表示

为了得到机械臂关节、末端的误差分布，将关节空间的协方差向笛卡尔空间映射，得到机械臂在笛卡尔空间下的误差特性。
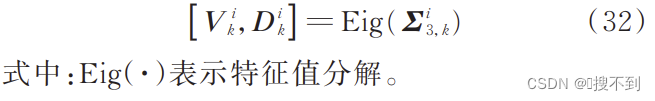
在这里插入图片描述

其中 $V_k^i$ 是特征值， $D_k^i$ 是特征矢量。

到达概率计算

在定义机器人运动的目标位置时会给出到达目的点的允许误差，例如：x_{goal} ± h。其中，x_{goal} 为目标位置，h 为允许的误差范围。

在三维空间中，机器人运动的目标区域范围可以看作是立方体，需要计算立方体的 6 个面与空间方差椭球之间的相关关系。
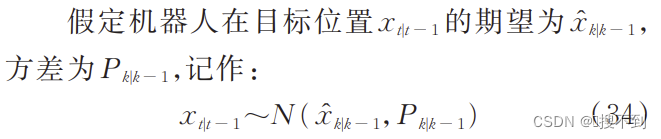
在这里插入图片描述
首先，只考虑概率分布 $x_{t|t - 1}$ 与第一个立方体平面约束 S_1 方程 $a_1^T x < b_1$ 范围内的概率分布和方差椭球缩放情况。

平面方程写成向量形式为 $a_1^T x = b_1$ ，其中 $a_1$ 为首个约束平面的法向单位矢量， $b_1$ 为平面方程的常量参数。

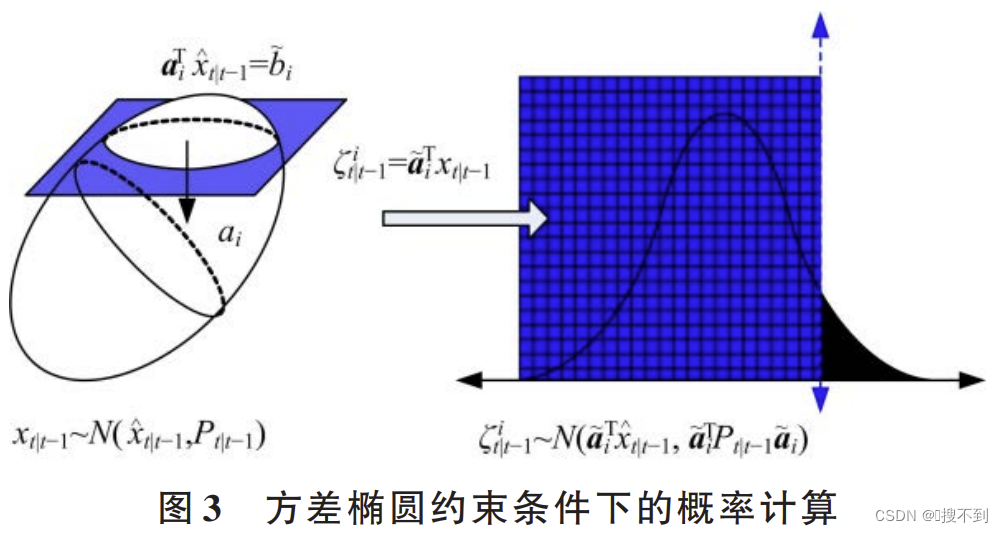
为了能将三维概率椭球投影到一维空间进行正态分布概率计算，逐个采用约束平面，对分布为 $x_{t|t - 1} \sim N(\hat{x}_{k|k - 1},P_{k|k - 1})$ 的概率椭圆（或椭球）进行剖分，并向一维空间投影得到正态分布，从而在一维空间下，进行满足限定约束条件的正态分布的概率计算，其计算方法示意图如图 3 所示。
在这里插入图片描述