单输入Doherty 功率放大器的极限带宽分析（含Matlab分析代码）

单输入Doherty 功率放大器的极限带宽分析（含Matlab分析代码）

参考论文：高效连续型射频功率放大器研究

DPA的基础理论参考：理想架构的Doherty功率放大器理论与仿真

1、单输入Doherty 功率放大器架构

假设 Doherty 功率放大器的中心频率为 f 0 f_{0} f0​，那么 Doherty 功放的合成网络由两根电长度分别为 θ 1 和 θ 2 \theta_1\text{和}\theta_2 θ1​和θ2​的微带线组成。这两个微带线有什么作用呢？其中TL1是为了在中心频率出呈现四分之一波长阻抗变换（理论参考理想架构的Doherty功率放大器理论与仿真），TL2是为了使得峰值支路在回退时不影响合路点（利用二分之一波长重复性将峰值功放不工作的无穷阻抗再次变换到无穷）。当然，如果TL2的长度为0，那么峰值功放在回退时对于合路点也是相当于无穷阻抗。
在这里插入图片描述
所以，无论上图中的m，n取何整数，都能在中心频率实现DPA调制。

2、非中心频率处的Doherty架构

2.1 TL2的影响

从理论上来讲，TL2的电长度只要是180°的整数倍都是能在中心频率处实现调制。TL2的作用主要是“利用二分之一波长重复性将峰值功放不工作的无穷阻抗再次变换到无穷”，从而减少峰值支路对载波功放的影响。

因此，我们希望TL2在非中心频率也能尽可能实现这一目的，尽可以实现二分之一波长的变换特性。先简单回顾一下一个基础知识，在 f 0 f_{0} f0​处电长度为180，那么在x f 0 f_{0} f0​处其等效电长度为x180。例如，在在 f 0 f_{0} f0​处电长度为180，那么在2 f 0 f_{0} f0​处其等效电长度为2180=360。

那么，对于n=1、2、3的情况有：
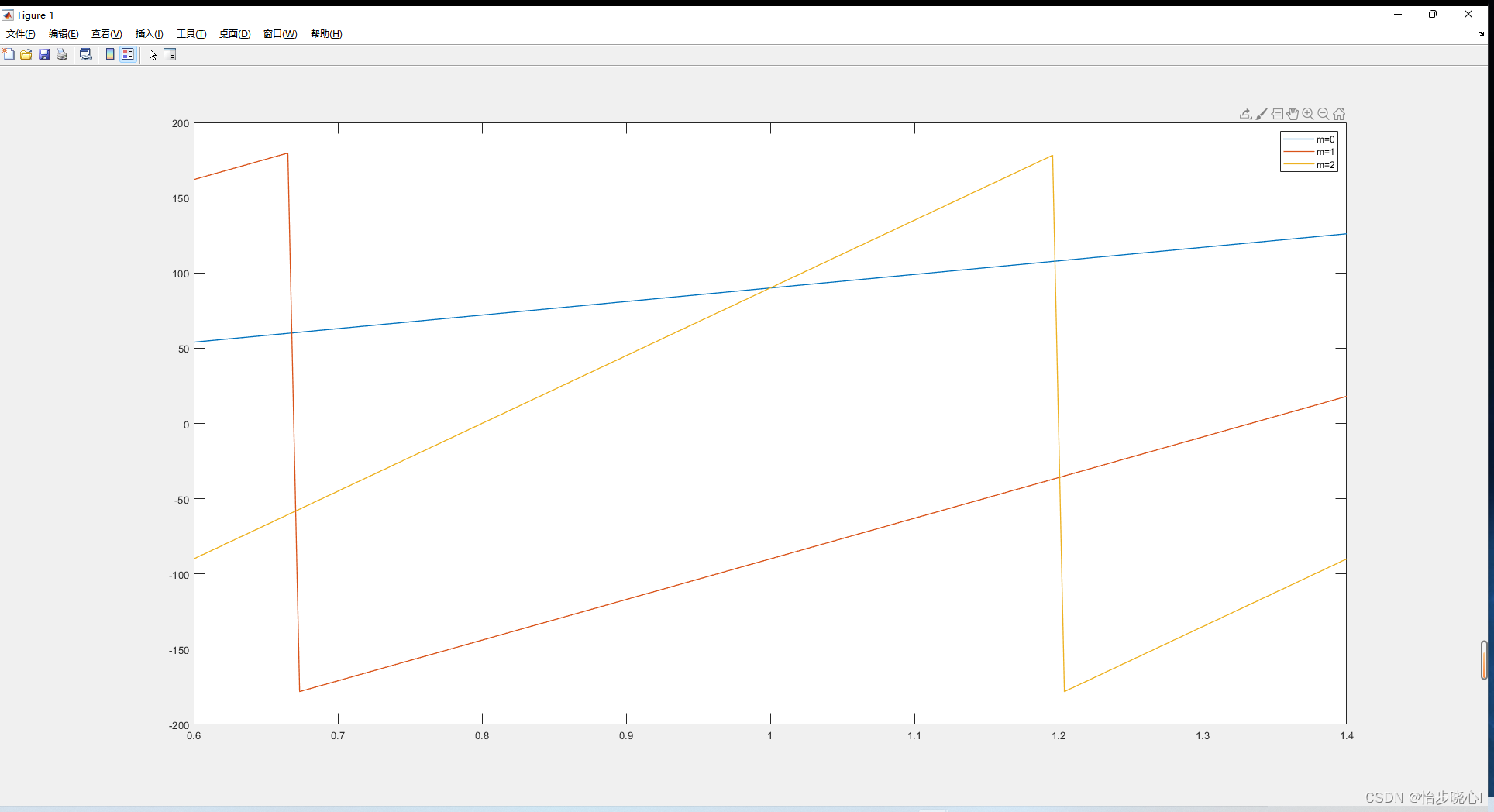
在这里插入图片描述
可以看到，n=0时在较宽范围内，其等效的电长度是比较接近90范围的。如果选择其他数值，延时的变化会非常剧烈，使用ADS仿真也会得到同样的效果。Matlab代码如下：

Ropt=1;
% 相对带宽表达式
f0=1;
f_arrary=f0*linspace(0.6, 1.4, 99);
figure(1)
for m=0:1:2theta_1=90+m*180;theta_1_f=theta_1*f_arrary/f0;while max(theta_1_f)>180theta_1_f(theta_1_f>180)=theta_1_f(theta_1_f>180)-360;endplot(f_arrary,theta_1_f,'LineWidth',1)hold on
end
legend('m=0','m=1','m=2')

2.2 TL1的影响

要想在回退取得高效率，其根源在于载波功放的输出阻抗ZCB的实部要是2*Ropt。那么ZCB如何求解表示呢？和两个微带线电长度的关系如何？下面进行求解

对于如下的回退电路图，峰值功放相当于开路，因此TL2相当于开路微带线。
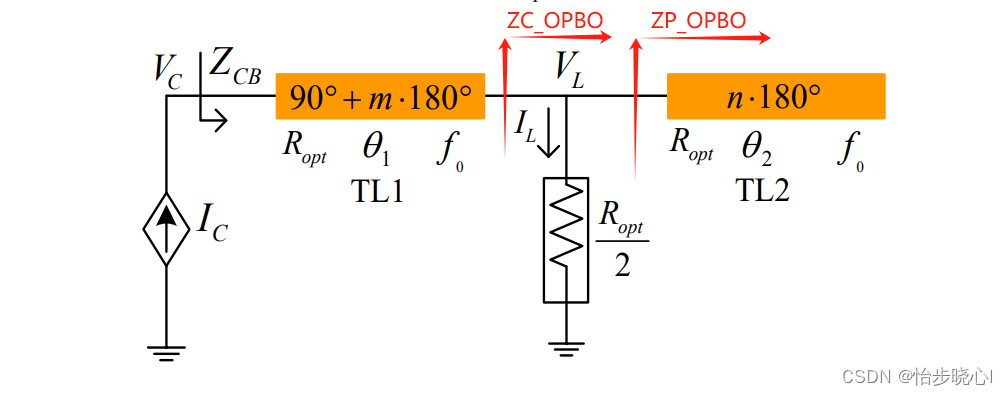
在这里插入图片描述

2.2.1 ZP_OPBO的阻抗计算

首先计算ZP_OPBO的阻抗，我们使用如下的式子，其中ZL是无穷，Z0是Ropt， β l \beta l βl就是电长度 θ 2 \theta_2 θ2​：
Z i n = Z 0 ⋅ Z L + j Z 0 tan β l Z 0 + j Z L tan β l Z_{in}=Z_0\cdot\frac{Z_L+jZ_0\text{tan}\beta l}{Z_0+jZ_L\text{tan}\beta l} Zin​=Z0​⋅Z0​+jZL​tanβlZL​+jZ0​tanβl​
那么新的计算式子就是：
Z P O P B O = R o p t ⋅ 1 j tan θ 2 ZP_{OPBO}=Ropt\cdot\frac{1}{j\text{tan}\theta_2} ZPOPBO​=Ropt⋅jtanθ2​1​
对应代码：

ZP_OPBO=Ropt./(1j*tand(theta_2_f));% 峰值负载为无穷
2.2.2 ZC_OPBO的阻抗计算

ZC_OPBO的阻抗等效于负载和ZP_OPBO并联，使用电阻并联的计算公式即可：
在这里插入图片描述
对应代码：

ZC_OPBO=1./(1/RL+1./ZP_OPBO);% 并联关系
2.2.3 ZCB的阻抗计算

使用公式：
Z i n = Z 0 ⋅ Z L + j Z 0 tan β l Z 0 + j Z L tan β l Z_{in}=Z_0\cdot\frac{Z_L+jZ_0\text{tan}\beta l}{Z_0+jZ_L\text{tan}\beta l} Zin​=Z0​⋅Z0​+jZL​tanβlZL​+jZ0​tanβl​
其中Zin就是ZCB，Z0就是TL1微带线的特性阻抗Ropt， β l \beta l βl就是电长度 θ 1 \theta_1 θ1​，ZL就是上面计算出来的ZC_OPBO，因此对应代码为：

ZCB=Ropt*(ZC_OPBO+1j*Ropt*tand(theta_1_f))./(Ropt+1j*ZC_OPBO.*tand(theta_1_f));% Zin计算

2.3 效率的计算

之前说过，要想在回退取得高效率，其根源在于载波功放的输出阻抗ZCB的实部要是2*Ropt。对于回退要求6dB的DPA来说，确实是这样的。

如果载波功放的输出阻抗小于2*Ropt，那么在6dB回退点没有饱和，效率低。

如果载波功放的输出阻抗大于2*Ropt，那么其会提前饱和，从而实现更大的回退，其在6dB处的效率也会低于理论效率78.54%的，因为中间会掉下来一块：
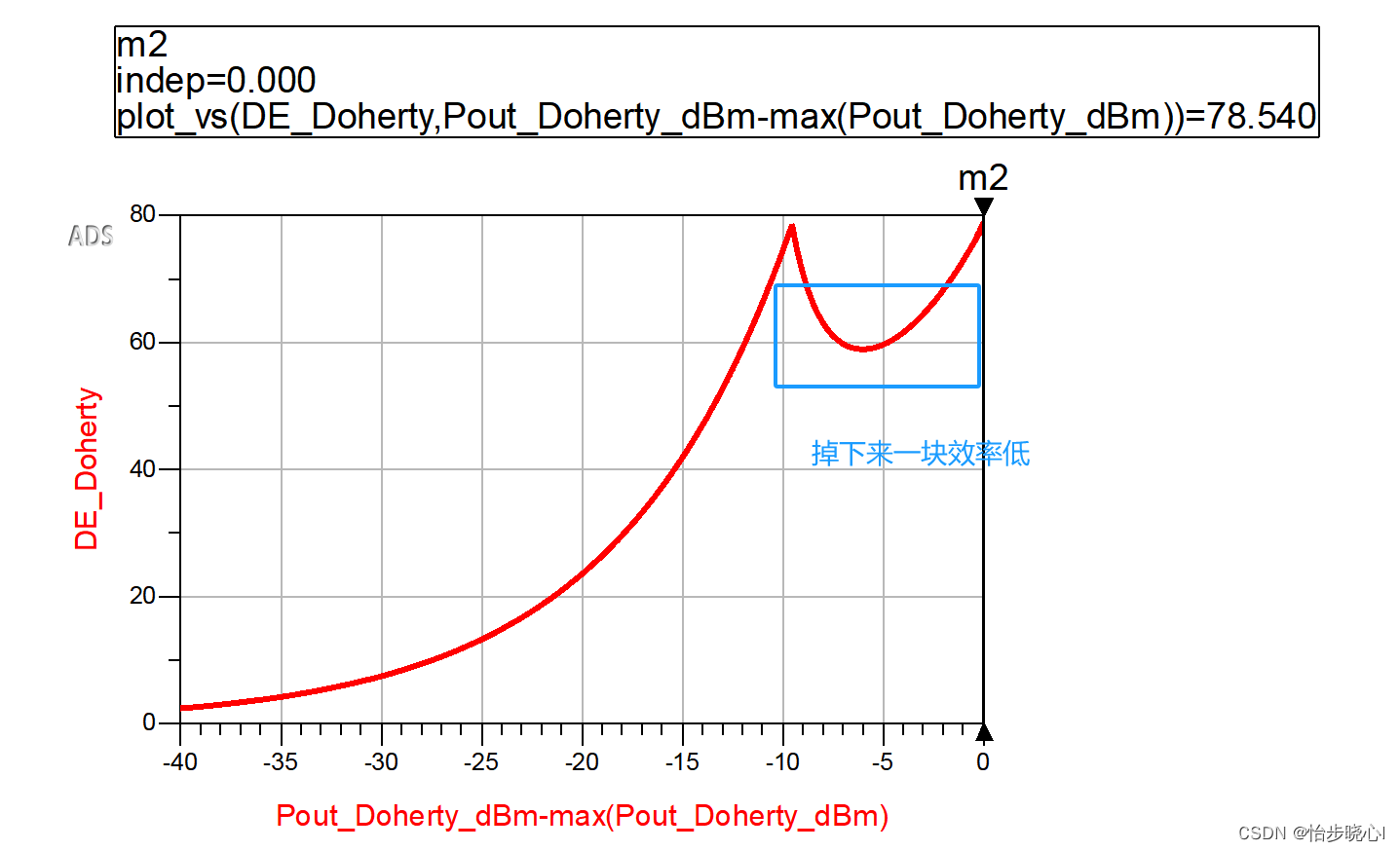
在这里插入图片描述
但是！在“高效连续型射频功率放大器研究”文中做出了如下定义，把载波功放的输出阻抗大于2*Ropt的效率当成78.54%，这也是为了方便比较。
对应代码如下：

    effi=78.54*real(ZCB)/(2*Ropt);% 计算效率，阻抗大于2Ropt被认为是饱和，效率为78.54effi(effi>78.54)=78.54;effi(isnan(effi))=78.54;

2.4 整体结果

可以看到，当选取m=0，n=1时候，带宽最高能够达到70%，这实际上也对应着连续B/J类的阻抗空间：
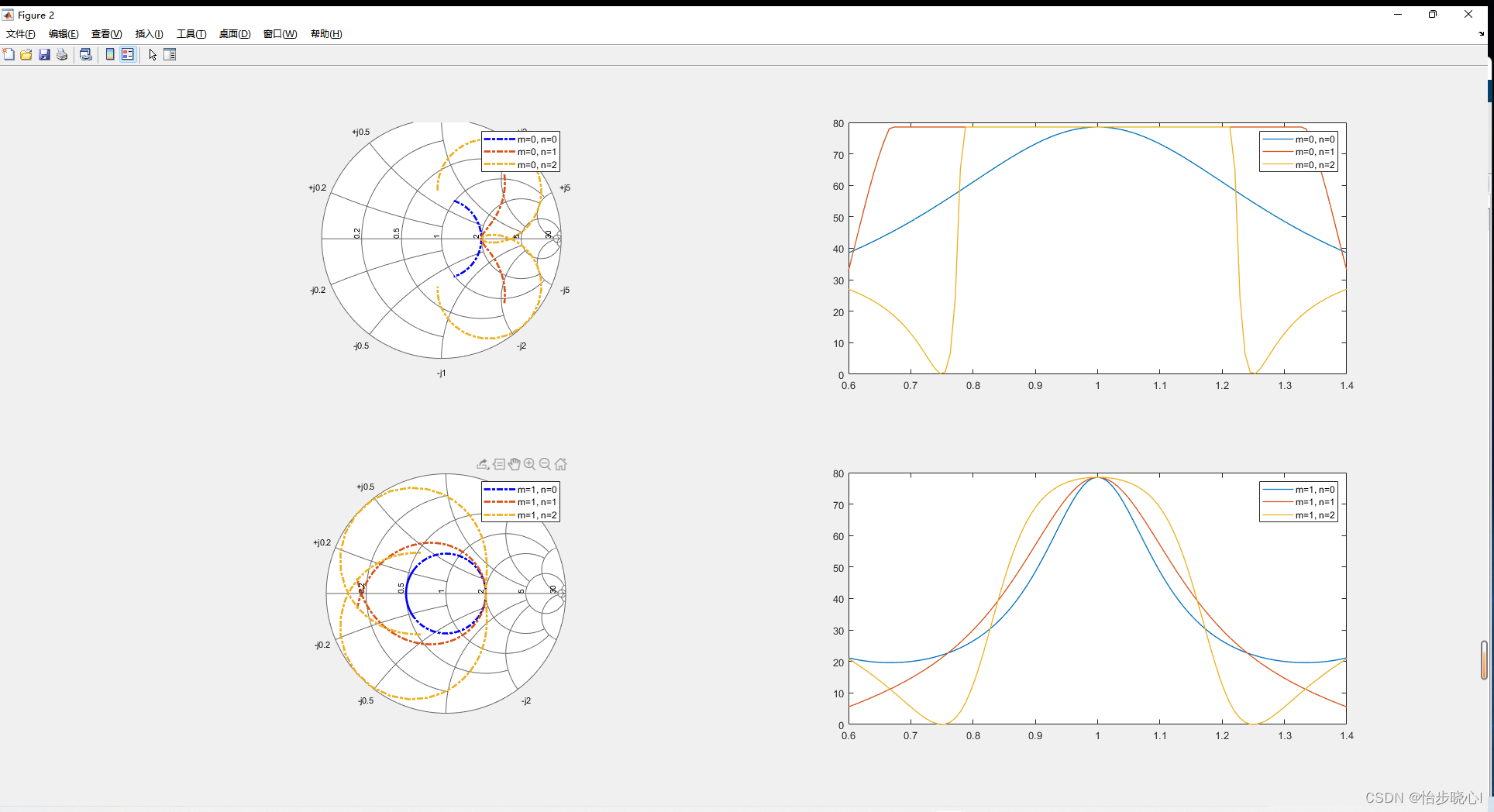
在这里插入图片描述

代码：

clc
clear
closeRopt=1;
% 相对带宽表达式
f0=1;
f_arrary=f0*linspace(0.6, 1.4, 99);
figure(1)
for m=0:1:2theta_1=90+m*180;theta_1_f=theta_1*f_arrary/f0;while max(theta_1_f)>180theta_1_f(theta_1_f>180)=theta_1_f(theta_1_f>180)-360;endplot(f_arrary,theta_1_f,'LineWidth',1)hold on
end
legend('m=0','m=1','m=2')% m=0,n=0\1\2
m=0;
theta_1=90+m*180+1e-10;
theta_1_f=theta_1*f_arrary/f0;
for n=0:1:2theta_2=n*180;theta_2_f=theta_2*f_arrary/f0+1e-10;ZP_OPBO=Ropt./(1j*tand(theta_2_f));% 峰值负载为无穷RL=Ropt/2;ZC_OPBO=1./(1/RL+1./ZP_OPBO);% 并联关系ZCB=Ropt*(ZC_OPBO+1j*Ropt*tand(theta_1_f))./(Ropt+1j*ZC_OPBO.*tand(theta_1_f));% Zin计算S_ZCB=(ZCB-1)./(ZCB+1);% Z参数转换S参数effi=78.54*real(ZCB)/(2*Ropt);% 计算效率，阻抗大于2Ropt被认为是饱和，效率为78.54effi(effi>78.54)=78.54;effi(isnan(effi))=78.54;figure(2)subplot(2,2,1)s = smithplot(S_ZCB,'Color','b','LineStyle','-.','LineWidth',2);hold onsubplot(2,2,2)plot(f_arrary,effi,'LineWidth',1)hold on
end
subplot(2,2,1)
legend('m=0, n=0','m=0, n=1','m=0, n=2')
subplot(2,2,2)
legend('m=0, n=0','m=0, n=1','m=0, n=2')% m=1,n=0\1\2
m=1;
theta_1=90+m*180+1e-10;
theta_1_f=theta_1*f_arrary/f0;
for n=0:1:2theta_2=n*180;theta_2_f=theta_2*f_arrary/f0+1e-10;ZP_OPBO=Ropt./(1j*tand(theta_2_f));% 峰值负载为无穷RL=Ropt/2;ZC_OPBO=1./(1/RL+1./ZP_OPBO);% 并联关系ZCB=Ropt*(ZC_OPBO+1j*Ropt*tand(theta_1_f))./(Ropt+1j*ZC_OPBO.*tand(theta_1_f));% Zin计算S_ZCB=(ZCB-1)./(ZCB+1);effi=78.54*real(ZCB)/(2*Ropt);effi(effi>78.54)=78.54;effi(isnan(effi))=78.54;figure(2)subplot(2,2,3)s = smithplot(S_ZCB,'Color','b','LineStyle','-.','LineWidth',2);hold onsubplot(2,2,4)plot(f_arrary,effi,'LineWidth',1)hold on
end
subplot(2,2,3)
legend('m=1, n=0','m=1, n=1','m=1, n=2')
subplot(2,2,4)
legend('m=1, n=0','m=1, n=1','m=1, n=2')

3 扫描角度结果

基于如上的把载波功放的输出阻抗大于2*Ropt的效率当成78.54 %的假设。

扫描两个微带线的电长度theta1和theta2，可以得到次优化 Doherty 工作模式的效率关系，也就是微带线的电长度不再需要遵循m、n是整数。

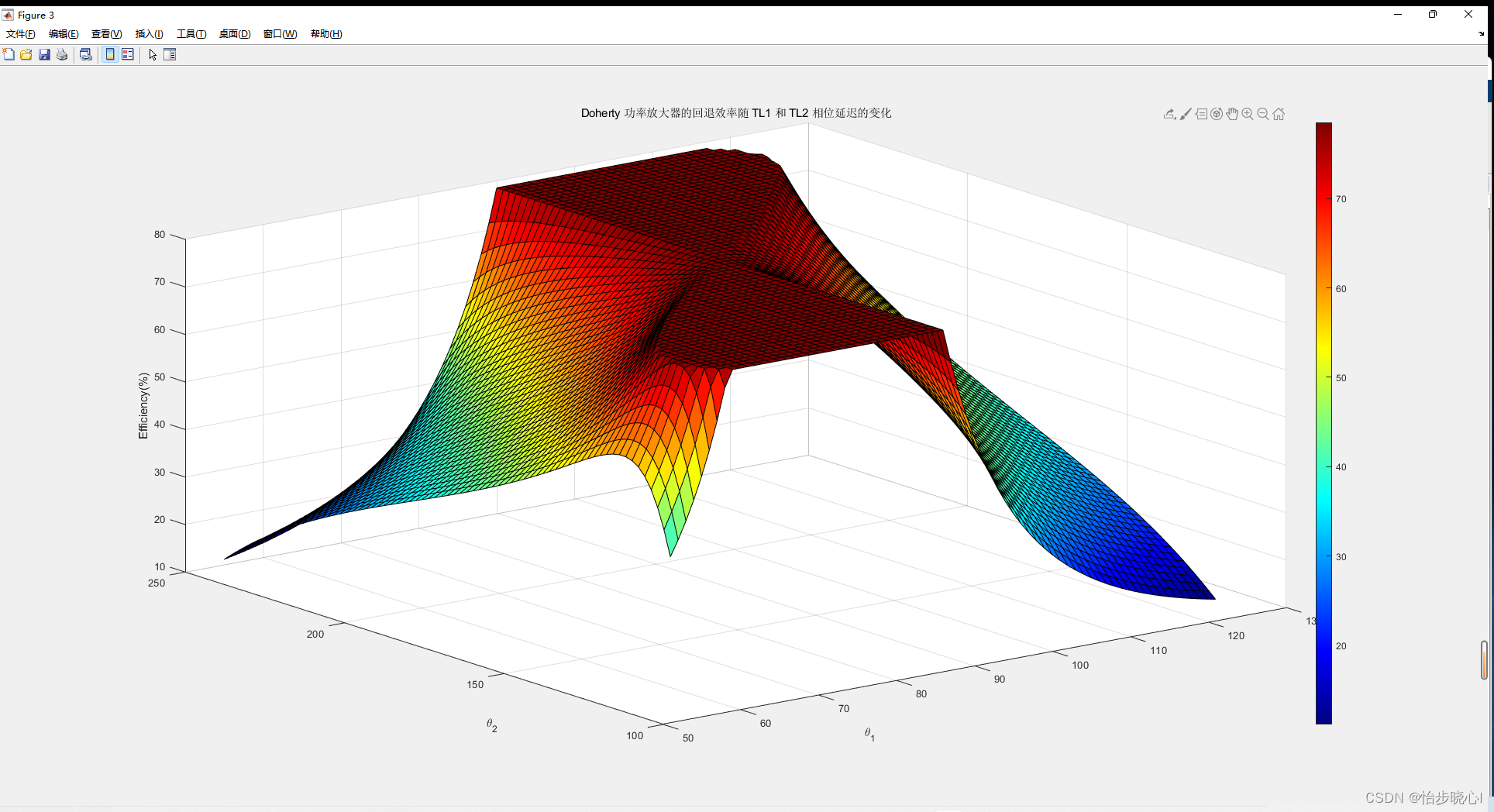
在这里插入图片描述

代码：

DPA_Effi_Cal.m：

function [effi] = DPA_Effi_Cal(theta_1,theta_2)Ropt=1;
RL=Ropt/2;
ZP_OPBO=Ropt./(1j*tand(theta_2));% 峰值负载为无穷
ZC_OPBO=1./(1/RL+1./ZP_OPBO);% 并联关系
ZCB=Ropt*(ZC_OPBO+1j*Ropt*tand(theta_1))./(Ropt+1j*ZC_OPBO.*tand(theta_1));% Zin计算
effi=78.54*real(ZCB)/(2*Ropt);% 计算效率，阻抗大于2Ropt被认为是饱和，效率为78.54
effi(effi>78.54)=78.54;
effi(isnan(effi))=78.54;
end

主函数：

clc
clear
close allRopt=1;
% 相对带宽表达式
f0=1;
f_arrary=f0*linspace(0.6, 1.4, 99);
figure(1)
for m=0:1:2theta_1=90+m*180;theta_1_f=theta_1*f_arrary/f0;while max(theta_1_f)>180theta_1_f(theta_1_f>180)=theta_1_f(theta_1_f>180)-360;endplot(f_arrary,theta_1_f,'LineWidth',1)hold on
end
legend('m=0','m=1','m=2')% m=0,n=0\1\2
m=0;
theta_1=90+m*180+1e-10;
theta_1_f=theta_1*f_arrary/f0;
for n=0:1:2theta_2=n*180;theta_2_f=theta_2*f_arrary/f0+1e-10;ZP_OPBO=Ropt./(1j*tand(theta_2_f));% 峰值负载为无穷RL=Ropt/2;ZC_OPBO=1./(1/RL+1./ZP_OPBO);% 并联关系ZCB=Ropt*(ZC_OPBO+1j*Ropt*tand(theta_1_f))./(Ropt+1j*ZC_OPBO.*tand(theta_1_f));% Zin计算S_ZCB=(ZCB-1)./(ZCB+1);% Z参数转换S参数effi=78.54*real(ZCB)/(2*Ropt);% 计算效率，阻抗大于2Ropt被认为是饱和，效率为78.54effi(effi>78.54)=78.54;effi(isnan(effi))=78.54;figure(2)subplot(2,2,1)s = smithplot(S_ZCB,'Color','b','LineStyle','-.','LineWidth',2);hold onsubplot(2,2,2)plot(f_arrary,effi,'LineWidth',1)hold on
end
subplot(2,2,1)
legend('m=0, n=0','m=0, n=1','m=0, n=2')
subplot(2,2,2)
legend('m=0, n=0','m=0, n=1','m=0, n=2')% m=1,n=0\1\2
m=1;
theta_1=90+m*180+1e-10;
theta_1_f=theta_1*f_arrary/f0;
for n=0:1:2theta_2=n*180;theta_2_f=theta_2*f_arrary/f0+1e-10;ZP_OPBO=Ropt./(1j*tand(theta_2_f));% 峰值负载为无穷RL=Ropt/2;ZC_OPBO=1./(1/RL+1./ZP_OPBO);% 并联关系ZCB=Ropt*(ZC_OPBO+1j*Ropt*tand(theta_1_f))./(Ropt+1j*ZC_OPBO.*tand(theta_1_f));% Zin计算S_ZCB=(ZCB-1)./(ZCB+1);effi=78.54*real(ZCB)/(2*Ropt);effi(effi>78.54)=78.54;effi(isnan(effi))=78.54;figure(2)subplot(2,2,3)s = smithplot(S_ZCB,'Color','b','LineStyle','-.','LineWidth',2);hold onsubplot(2,2,4)plot(f_arrary,effi,'LineWidth',1)hold on
end
subplot(2,2,3)
legend('m=1, n=0','m=1, n=1','m=1, n=2')
subplot(2,2,4)
legend('m=1, n=0','m=1, n=1','m=1, n=2')% 绘制角度和效率的等高图
figure(3)
x=55:1:125;y=110:2:250;
[X,Y] = meshgrid(x,y);for i=1:1:length(X)for j=1:1:length(X)Z(i,j)=DPA_Effi_Cal(X(i,j),Y(i,j));end
end
surf(X,Y,Z);
title('Doherty 功率放大器的回退效率随 TL1 和 TL2 相位延迟的变化')
colormap jet%summer是一种配色方案，还有其他方案如winter，summer····见help colormap
colorbar
xlabel('\theta_1');
ylabel('\theta_2');
zlabel('Efficiency(%)');
% axis([-0.5 0.5 -1 1 -1.5 1.5]);

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/688189.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

介绍7款免费的最佳地图/导航/定位/GIS开源项目

介绍7款免费的最佳地图/导航/定位/GIS开源项目

文章目录 1、xdh-map新德汇地图应用类库1.1、独立引用1.2、与MyUI结合使用1.3、快速上手1.3.1、采用项目工程模板创建项目【推荐】1.3.2、 调用组件库功能 2、蚂蚁金服AntV-L7地理空间数据可视分析引擎2.1、AntV-L7简介2.2、核心特性2.3、支持丰富的图表类型2.4、如何使用2.4.1…
阅读更多...
BLHeli_S 代码分析—BLHeli.asm函数 init_start_bidir_done 分析

BLHeli_S 代码分析—BLHeli.asm函数 init_start_bidir_done 分析

BLHeli_S 代码分析—BLHeli.asm函数init_start_bidir_done分析 init_start_bidir_done代码 代码中数据变量定义 Flags1: DS 1 ; 状态标志. Reset upon init_start 初始化启动时重置 MOTOR_SPINNING EQU 0 ; 电机旋转标志 STARTUP_PHASE EQU 1 ; 启动相位标志Startup_…
阅读更多...
反转一个单链表

反转一个单链表

反转一个单链表 题意：反转一个单链表。 示例: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL 思路 需要虚拟节点么？ 答：不需要，因为没有删除节点，只是改变了节点的指向。 遍…
阅读更多...
STM32-开发环境之STM32CubeMX

STM32-开发环境之STM32CubeMX

目录 STM32CubeMX介绍 STM32CubeMX特性 应用场景 其他事项 STM32CubeMX介绍 STM32CubeMX是ST公司（意法半导体）推出的一款图形化工具，也是配置和初始化C代码生成器。它主要服务于STM32微控制器的配置和开发。 STM32CubeMX特性 1.直观选…
阅读更多...
计算机设计大赛 深度学习二维码识别

计算机设计大赛 深度学习二维码识别

文章目录 0 前言2 二维码基础概念2.1 二维码介绍2.2 QRCode2.3 QRCode 特点 3 机器视觉二维码识别技术3.1 二维码的识别流程3.2 二维码定位3.3 常用的扫描方法 4 深度学习二维码识别4.1 部分关键代码 5 测试结果6 最后 0 前言 🔥 优质竞赛项目系列，今天…
阅读更多...
Rust-知多少？

Rust-知多少？

文章目录 前言1.使用下划线开头忽略未使用的变量2. 变量解构3.常量4.变量遮蔽（shadowing）5. 类似println!("{}", x); 为啥加感叹号6.单元类型总结 前言 Rust 学习系列，记录一些rust使用小技巧 1.使用下划线开头忽略未使用的变量 …
阅读更多...
MySQL跨服务器关联查询

MySQL跨服务器关联查询

1. 首先确认服务器的Federated引擎是否开启 show engines;修改数据库的配制文件my.ini,(我的my.ini的路径为：D:\ProgramData\MySQL\MySQL Server 5.7/my.ini),将federated添加到my.ini文件中 到MySQL的my.cnf配置文件中修改 在 [mysqld] 下方加入 federated 然后重…
阅读更多...
通过前序和中序遍历结果构造二叉树

通过前序和中序遍历结果构造二叉树

题目 105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode） 思路 首先思考，根节点应该做什么。 肯定要想办法确定根节点的值，把根节点做出来，然后递归构造左右子树即可。 我们先来回顾一下，前序遍历和…
阅读更多...
CF1781 D. Many Perfect Squares [数学题]

CF1781 D. Many Perfect Squares [数学题]

传送门:CF [前题提要]:一道有意思的数学题 直接想这道题是不好想的(博主当时就完全没有思路).那么考虑将一个大问题分解成一个小问题想一下(感觉这种思考方式在CF题中还是挺常见的),考虑如果同时存在多个完全平方数,那么必然满足存在两个完全平方数.而当我们确定了任意两个数之…
阅读更多...
全网超全的测试类型详解，再也不怕面试答不出来了！

全网超全的测试类型详解，再也不怕面试答不出来了！

在软件测试工作过程中或者在面试过程中经常会被问到一些看起来简单但是总是有些回答不上的问题，比如你说说“黑盒测试和白盒测试的区别？”，“你们公司做灰度测试么？", ”α测试和β测试有什么不一样？“&#xff0…
阅读更多...
文件 IO

文件 IO

一，标准IO和文件IO的区别 1.标准IO是库函数，是对系统调用的封装 2.文件IO是系统调用，时linux内核中的函数接口 3.标准IO是有缓存的，文件IO是没有缓存的（实时性强） 二，文件IO 1.三步操作&…
阅读更多...
review 10

review 10

整理磁盘操作的完整流程，如何接入虚拟机，是否成功识别，对磁盘分区工具的使用，格式化，挂载以及取消挂载、复习cp、mv和find指令 1：U盘接入虚拟机 在弹出窗口直接选择 虚拟机-可移动设备-找到u盘-连接 2&a…
阅读更多...
【Ubuntu 22.04】解决Ubuntu 22.04终端行距过大的问题

【Ubuntu 22.04】解决Ubuntu 22.04终端行距过大的问题

在Ubuntu 22.04中，许多用户都遇到了终端行距过大的问题，不论是使用 GNOME 终端还是 Terminator，都存在这个困扰。这个问题导致显示的内容的行距很大，比如执行 neofetch 命令时，Ubuntu LOGO被拉长。 经过查询&#xff…
阅读更多...
matlab代码--基于注水法的MIMO信道容量实现

matlab代码--基于注水法的MIMO信道容量实现

今天接触一个简单的注水法程序，搞懂数学原理即可看懂代码。 1 注水法简介 详细原理可以参考： MIMO的信道容量以及实现 大致理论就是利用拉格朗日乘子法，求解信道容量的最大化问题，得到的解形如往水池中注水的形式，最…
阅读更多...
过字符设备驱动分步注册过程实现LED驱动的编写，编写应用程序测试，发布到CSDN

过字符设备驱动分步注册过程实现LED驱动的编写，编写应用程序测试，发布到CSDN

头文件 #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct{unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int ODR; }gpio_t; #define PHY_LED1_ADDR 0X50006000 #define PHY_LED2_ADDR 0X50007000 #d…
阅读更多...
信号系统之移动平均滤波器

信号系统之移动平均滤波器

1 通过卷积实现 移动平均滤波器的工作原理是平均输入信号中的多个点，以产生输出信号中的每个点。在方程式形式中，这样写： 其中是 x 输入信号，y 是输出信号，M 是平均值中的点数。例如，在 5 点移动平均滤波器…
阅读更多...
基于51单片机的智能台灯的设计与实现

基于51单片机的智能台灯的设计与实现

摘 要：针对青少年因坐姿不正确、灯光亮度不合适、用眼过度等原因易导致的近视问题，文中提出使用51单片机作为主控制单元，选用红外检测、光敏检测、蓝牙通信、蜂鸣器和模数转换等模块，设计了一款智能台灯。该智能台灯具有节能、预防近视等功能。经测试，该台灯具有保护视力的…
阅读更多...
php基础学习之常用系统函数

php基础学习之常用系统函数

一，有关输出的语句/函数 echo语句 用于输出一个或多个字符串 print语句 用于输出一个字符串（用句点连接的多个字符串本质是一个字符串），与echo类似，但返回值为1 printf()函数 用于格式化输出字符串，类似于C…
阅读更多...
Android下SF合成流程重学习之Refresh流程

Android下SF合成流程重学习之Refresh流程

Android下SF合成流程重学习之Refresh流程 引言 在前面初步分析完成了Android下SF合成流程重学习之Invalidate流程，我们接下来继续下面的分析。当有事务的更新或者有Buffer的更新便会触发后面刷新的流程,即Refresh流程！ 一. onMessageRefresh 文件&…
阅读更多...
QT串口通讯上位机_基础串口通讯

QT串口通讯上位机_基础串口通讯

目录 1. 实现目标1.1 界面1.2 发送1.3 接收1.4 清除接收、发送 2. 新建工程3. 添加头文件4. 变量定义5. 完整代码6. 工程下载 1. 实现目标 1.1 界面 1.2 发送 1.3 接收 1.4 清除接收、发送 2. 新建工程 3. 添加头文件 QT serialport // #include <QDebug‘’> #incl…
阅读更多...
最新文章

Copyright @ 2022~2023