Unity基础

3D数学 – 基础

一些方法

float value01 = Mathf.PI; // Π
int value03 = Mathf.Abs(-2); // 绝对值
int value04 = Mathf.CeilToInt(1.3f); // 向上取整
int value05 = Mathf.FloorToInt(1.6f); // 向下取整
int value06 = Math.Clamp(5, 10, 20); // 钳制函数：在10~20直接返回值，10~20之外返回接近的那个值
int value07 = Mathf.Min(10, 90, 2); // 最小值,参数可变长
int value08 = Mathf.Max(1, 2, 6); // 最大值,参数可变长
float value09 = Mathf.Pow(5, 2); // 幂运算
int value10 = Mathf.RoundToInt(1.5f); // 四舍五入
float value11 = Mathf.Sqrt(4.0f); // 平方根      

插值运算

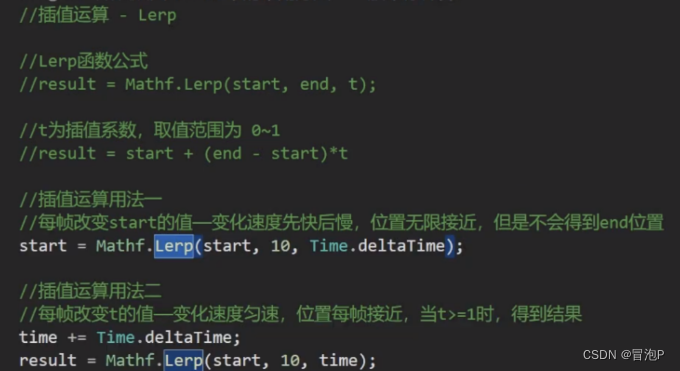
三角函数

​

	// 弧度转角度float rad = 5;float anger = 5 * Mathf.Rad2Deg;// 角度转弧度anger = 1;rad = anger * Mathf.Deg2Rad;// 三角函数：参数是弧度值anger = 30 * Mathf.Deg2Rad;float sin30rad = Mathf.Sin(anger);// 反三角函数：返回值是弧度值float asin = Mathf.Asin(1);print(asin * Mathf.Rad2Deg);

坐标系

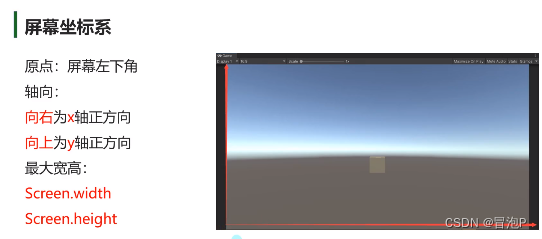
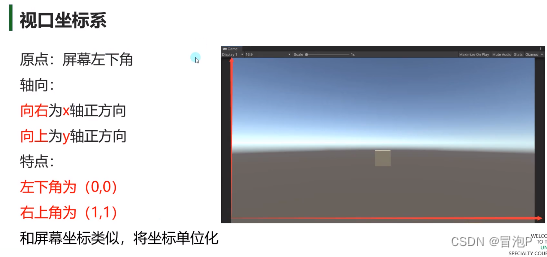
3D数学 – 向量

理解

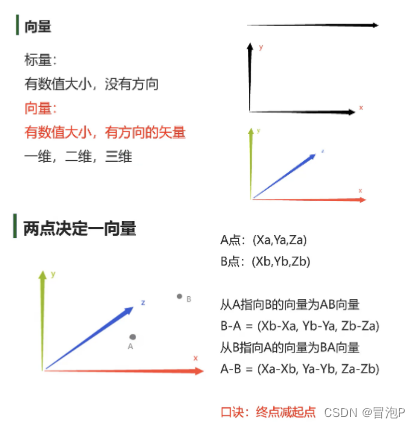
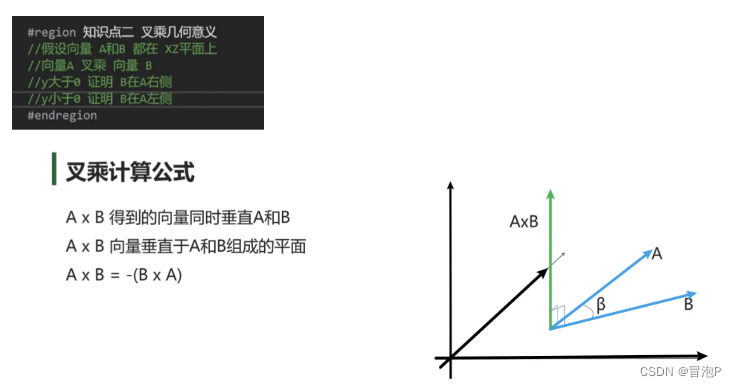
常用函数

// 点乘
Vector3.Dot(dir1, dir2);// 叉乘
Vector3.Cross(dir1, dir2);// 角度
Vector3.Angle(dir1, dir2);// 两点间距离
Vector3.Distance(pos1, pos2);

线性插值

与Mathf.Lerp用法相同，只是参数为Vector3

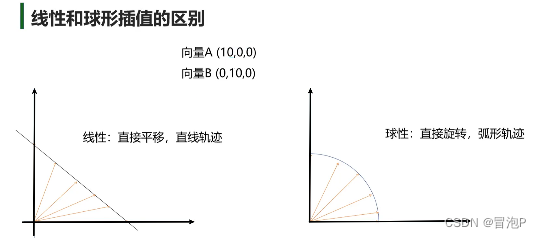
3D数学 – 四元数

// 初始化四元数Quaternion q = Quaternion.AngleAxis(60, Vector3.right);this.transform.rotation = q;// 欧拉角转四元数Vector3 euler = new Vector3(1, 2, 3);Quaternion qua = Quaternion.Euler(euler);// 四元数转欧拉角euler = qua.eulerAngles;

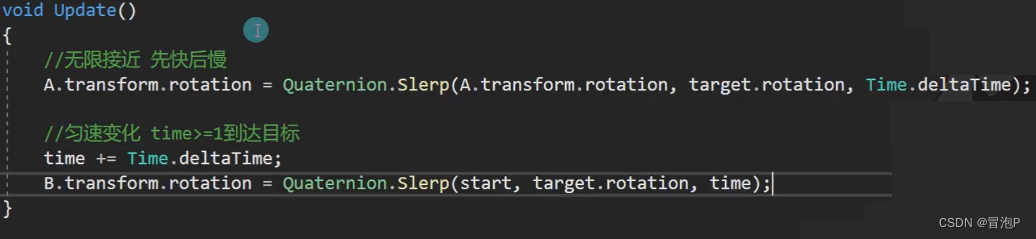
看向

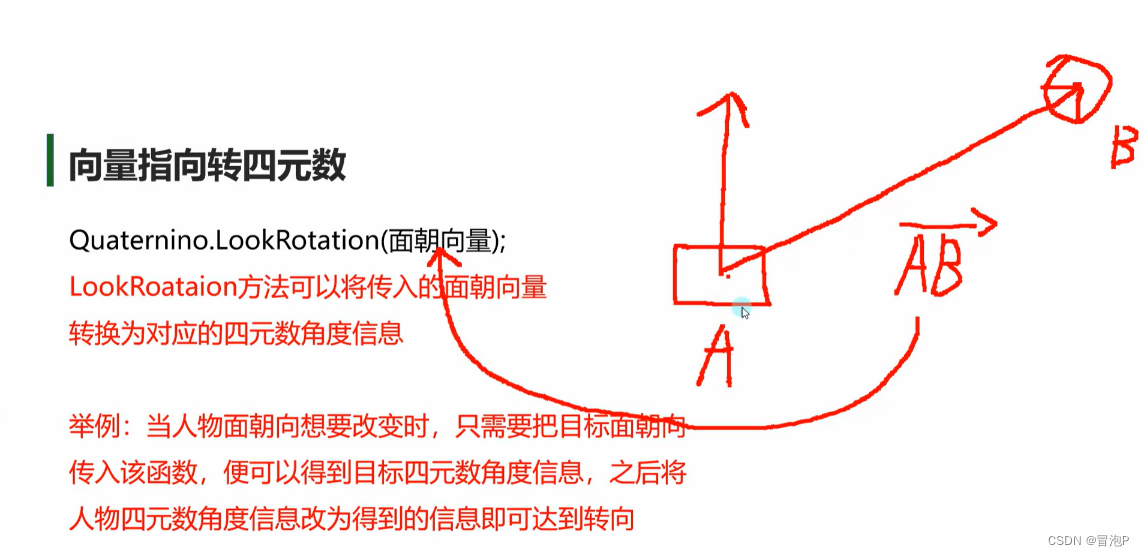
四元数计算

延迟函数

1. 延迟函数

   参数一：函数名 字符串 参数二：延迟时间 单位秒

   注意：延迟函数无法直接调用有参函数，函数名必须是该脚本申明的函数

   Invoke("function", 5);
   

2. 延迟重复执行函数

   参数一：函数名 字符串 参数二：第一次执行延迟时间 参数三：之后每次执行的间隔时间

   注意：同上

   InvokeRepeating("function", 5, 5);
   

3. 取消延迟函数

   CancelInvoke(); // 取消该脚本上所有延迟函数
   CancelInvoke("function"); // 取消指定函数名的延迟函数
   

4. 判断是否有延迟函数

   bool isInvoke = IsInvoking();
   bool isInvoke2 = IsInvoking("function");
   

影响延迟函数：

脚本依附对象失活、脚本失活，延迟函数继续执行

脚本依附对象销毁、脚本销毁，延迟函数继续执行

协同程序

1. 多线程

   注意：新开的线程无法访问Unity相关对象的内容

   Thread th;void Start()
   {th = new Thread(Test); // 创建线程th.Start(); // 开启线程
   }// 线程与Unity编辑器共存亡，所以需要关闭线程
   private void OnDestroy() 
   {th.Abort(); // 结束线程th = null;    
   }private void Test()
   {while(true){Thread.Sleep(1000);print("Thread");}
   }
   

2. 协同程序（协程）

   • “假”的多线程，协程不是多线程

   • 将代码分时执行

   • 使用场景：异步加载、下载，场景异步加载，批量创建防止卡顿

   • 与线程的区别：

     ​ 线程：新开一个独立的管道和主线程并行执行

     ​ 协程：新开一个协程在原线程之上开启，进行逻辑的分时分步执行