2.15学习总结

2.15
1.聪明的质监员（二分+前缀和）
2.村村通（并查集）
3.玉蟾宫(悬线法DP)
4.随机排列（树状数组逆序对问题）
5.增进感情（DFS）

6.医院设置（floyd）

聪明的质监员https://www.luogu.com.cn/problem/P1314

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 �n 个矿石，从 11 到 �n 逐一编号，每个矿石都有自己的重量 ��wi 以及价值 ��vi 。检验矿产的流程是：

给定�m 个区间 [��,��][li,ri]；

选出一个参数 �W；

对于一个区间 [��,��][li,ri]，计算矿石在这个区间上的检验值 ��yi：

��=∑�=��[��≥�]×∑�=��[��≥�]��yi=j=li∑ri[wj≥W]×j=li∑ri[wj≥W]vj

其中 �j 为矿石编号。

这批矿产的检验结果 �y 为各个区间的检验值之和。即：∑�=1��i=1∑myi

若这批矿产的检验结果与所给标准值 �s 相差太多，就需要再去检验另一批矿产。小T 不想费时间去检验另一批矿产，所以他想通过调整参数 �W 的值，让检验结果尽可能的靠近标准值 �s，即使得 ∣�−�∣∣s−y∣ 最小。请你帮忙求出这个最小值。

输入格式

第一行包含三个整数 �,�,�n,m,s，分别表示矿石的个数、区间的个数和标准值。

接下来的 �n 行，每行两个整数，中间用空格隔开，第 �+1i+1 行表示 �i 号矿石的重量 ��wi 和价值 ��vi。

接下来的 �m 行，表示区间，每行两个整数，中间用空格隔开，第 �+�+1i+n+1 行表示区间 [��,��][li,ri] 的两个端点 ��li 和 ��ri。注意：不同区间可能重合或相互重叠。

输出格式

一个整数，表示所求的最小值。

输入输出样例

输入 #1复制

5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3

输出 #1复制

10

说明/提示

【输入输出样例说明】

当 �W 选 44 的时候，三个区间上检验值分别为 20,5,020,5,0 ，这批矿产的检验结果为 2525，此时与标准值 �S 相差最小为 1010。

【数据范围】

对于 10%10% 的数据，有 1≤�,�≤101≤n,m≤10；

对于 30%30%的数据，有 1≤�,�≤5001≤n,m≤500 ；

对于 50%50% 的数据，有 1≤�,�≤5,0001≤n,m≤5,000；

对于 70%70% 的数据，有 1≤�,�≤10,0001≤n,m≤10,000 ；

对于 100%100% 的数据，有 1≤�,�≤200,0001≤n,m≤200,000，0<��,��≤1060<wi,vi≤106，0<�≤10120<s≤1012，1≤��≤��≤�1≤li≤ri≤n 。

思路：每次找的时候用前缀和存，不然会TLE

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=2e5+5;int n,m,s,min1=INF,maxn,minn=INF,sum,ans;	//矿石，区间，标准值int w[N],v[N],l[N],r[N],pre_v[N],pre_n[N];bool check(int k){ans=0,sum=0;memset(pre_v,0,sizeof(pre_v));memset(pre_n,0,sizeof(pre_n));for (int i=1;i<=n;++i){if (w[i]>=k){pre_v[i]=pre_v[i-1]+v[i];pre_n[i]=pre_n[i-1]+1;}else{pre_v[i]=pre_v[i-1];pre_n[i]=pre_n[i-1];}}for (int i=1;i<=m;++i){ans+=(pre_n[r[i]]-pre_n[l[i]-1])*(pre_v[r[i]]-pre_v[l[i]-1]);}sum=abs(ans-s);if (ans>s) return true;else return false;
}signed main(){cin>>n>>m>>s;for (int i=1;i<=n;++i){cin>>w[i]>>v[i];maxn=max(maxn,w[i]);minn=min(minn,w[i]);} for (int i=1;i<=m;++i){cin>>l[i]>>r[i];}minn=minn-1,maxn=maxn+2;while (minn<=maxn){int mid=minn+maxn>>1;if (check(mid)) minn=mid+1;else maxn=mid-1;if (sum<min1) min1=sum;}cout<<min1;
}

村村通https://www.luogu.com.cn/problem/P1536

题目描述

某市调查城镇交通状况，得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府 "村村通工程" 的目标是使全市任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要相互之间可达即可）。请你计算出最少还需要建设多少条道路？

输入格式

输入包含若干组测试数据，每组测试数据的第一行给出两个用空格隔开的正整数，分别是城镇数目 �n 和道路数目 �m ；随后的 �m 行对应 �m 条道路，每行给出一对用空格隔开的正整数，分别是该条道路直接相连的两个城镇的编号。简单起见，城镇从 11 到 �n 编号。

注意：两个城市间可以有多条道路相通。

在输入数据的最后，为一行一个整数 00，代表测试数据的结尾。

输出格式

对于每组数据，对应一行一个整数。表示最少还需要建设的道路数目。

输入输出样例

输入 #1复制

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

输出 #1复制

1
0
2
998

说明/提示

数据规模与约定

对于 100%100% 的数据，保证 1≤�<10001≤n<1000 。

思路：并查集，把所有的关系都连接起来，然后遍历所有情况，找到没有连接的，计数器自增

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=2e5+5;int f[N],n,m,cnt,p;int find(int x){if (f[x]==x) return x;else if (f[x]!=x){f[x]=find(f[x]);return f[x];}
}void merge(int i,int j){f[find(i)]=find(j);
}signed main(){while (1){cnt=0;cin>>n;if (n==0) return 0;cin>>m;for (int i=1;i<=n;++i) f[i]=i;for (int i=0;i<m;++i){int a,b;p=a;cin>>a>>b;merge(a,b);}for (int i=1;i<=n;++i){if (find(i)!=find(p)){cnt++;merge(i,p);}}cout<<cnt<<endl;;}
}

玉蟾宫https://www.luogu.com.cn/problem/P4147

题目背景

有一天，小猫 rainbow 和 freda 来到了湘西张家界的天门山玉蟾宫，玉蟾宫宫主蓝兔盛情地款待了它们，并赐予它们一片土地。

题目描述

这片土地被分成 �×�N×M 个格子，每个格子里写着 'R' 或者 'F'，R 代表这块土地被赐予了 rainbow，F 代表这块土地被赐予了 freda。

现在 freda 要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着 'F' 并且面积最大。

但是 rainbow 和 freda 的 OI 水平都弱爆了，找不出这块土地，而蓝兔也想看 freda 卖萌（她显然是不会编程的……），所以它们决定，如果你找到的土地面积为 �S，它们每人给你 �S 两银子。

输入格式

第一行两个整数 �N，�M，表示矩形土地有 �N 行 �M 列。

接下来 �N 行，每行 �M 个用空格隔开的字符 'F' 或 'R'，描述了矩形土地。

输出格式

输出一个整数，表示你能得到多少银子，即 (3×最大 ’F’ 矩形土地面积3×最大 ’F’ 矩形土地面积) 的值。

输入输出样例

输入 #1复制

5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F

输出 #1复制

45

说明/提示

对于 50%50% 的数据，1≤�,�≤2001≤N,M≤200。
对于 100%100% 的数据，1≤�,�≤10001≤N,M≤1000。

思路：用悬线法写，l数组存每个点向左最多可以到哪里，r数组为右，h数组存的是向上最多可以到哪里，但是在找h数组的时候，需要同时判断垂直的点，lr数组的关系

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=1010;int h[N][N],m,n,l[N][N],r[N][N];
char a[N][N];signed main(){cin>>n>>m;for (int i=1;i<=n;++i){for (int j=1;j<=m;++j){cin>>a[i][j];if (a[i][j]=='F')h[i][j]=1;l[i][j]=j;r[i][j]=j;}}for (int i=1;i<=n;++i){for (int j=2;j<=m;++j){if (a[i][j]=='F' && a[i][j-1]=='F'){l[i][j]=l[i][j-1];}}for (int j=m-1;j>=1;--j){if (a[i][j]=='F' && a[i][j+1]=='F'){r[i][j]=r[i][j+1];}}}int ans=0;for (int i=1;i<=n;++i){for (int j=1;j<=m;++j){if (a[i][j]=='F' && a[i-1][j]=='F'){h[i][j]=h[i-1][j]+1;l[i][j]=max(l[i][j],l[i-1][j]);r[i][j]=min(r[i][j],r[i-1][j]);}if (a[i][j]=='F')ans=max(ans,(r[i][j]-l[i][j]+1)*h[i][j]);}}cout<<ans*3;
}

随机排列https://www.acwing.com/problem/content/5469/

给定一个 1∼n1∼� 的排列 a1,a2,…,an�1,�2,…,��。

我们规定，交换操作指从排列中随机选择两个不同元素并交换彼此位置。

给定两种打乱排列的方式：

对排列连续进行 3n3� 次交换操作。
对排列连续进行 7n+17�+1 次交换操作。

已知，给定排列 a1∼an�1∼�� 就是由 1,2,…,n1,2,…,� 经过上述两种打乱方式之一得到的。

请你判断，给定排列具体是由哪一种打乱方式得到的。

输入格式

第一行包含整数 n�。

第二行包含 n� 个整数 a1,a2,…,an�1,�2,…,��。

输出格式

如果给定排列是由方式 11 打乱得到的，则输出 11，如果给定排列是由方式 22 打乱得到的，则输出 22。

保证给定排列一定是由两种打乱方式之一得到的。

数据范围

前 33 个测试点满足 2≤n≤102≤�≤10。
所有测试点满足 2≤n≤1062≤�≤106，保证 a1∼an�1∼�� 是一个 1∼n1∼� 的排列。

输入样例：
5
2 4 5 1 3
输出样例：
1

思路：本质上是找逆序数，由于每次改变都会改变逆序数的奇偶性，所以，当前数组的逆序数个数的奇偶性与改变次数的奇偶性相同

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 1e6+5;
int tr[N],w[N];int lowbit(int x){return x & -x;
}void update(int x, int k){while(x<=N){tr[x]+=k;x+=lowbit(x);}
}int query(int x){int res=0;while (x>0){res+=tr[x];x-=lowbit(x);}return res;
}int main()
{int n;cin>>n;int res=0;for (int i = 0; i < n; ++ i ){int x;cin>>x;res=(res+query(n)-query(x))%2;update(x,1);}if (res== 3*n%2) cout<<1;else cout << 2;
}

增进感情https://www.luogu.com.cn/problem/P2080

题目背景

小明和小红的感情，是慢慢发展起来的。

题目描述

他们对对方分别有一个好感值。定义两人的亲密程度为两人的好感值之和。

如果他们的亲密程度达到 �v，则他们将走到一起。他们以后的生活将取决于两人的好感值之差的绝对值，这个值越小，他们的生活将越幸福。

现在，他们对对方的好感值都为 00，小明有 �n 件事可以干，每件事可以增加他对小红的好感 ��ai 点，并且增加小红对他的好感 ��bi 点。（可能为负数）

小明可以任选一些事做，请你帮小明求出怎样才能让他们的生活更加幸福（求出两人在一起的前提下，好感值之差的最小绝对值即可）。

输入格式

第一行，两个正整数 �,�n,v。

之后 �n 行，每行两个空格隔开的整数 ��,��ai,bi。

输出格式

一行，一个非负整数，表示两人在一起的前提下，好感值之差的最小绝对值。如果无论如何两人也无法在一起，输出 -1。

输入输出样例

输入 #1复制

4 15
5 6
-1 8
7 2
1 0

输出 #1复制

3

说明/提示

数据范围与约定

对于 20%20% 数据，保证 �≤10n≤10。

对于 100%100% 数据，保证 1≤�≤301≤n≤30，1≤∣��∣,∣��∣≤1001≤∣ai∣,∣bi∣≤100。

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3fconst int N=35;int n,v,ans=INF,l,r;
int a[N],b[N],vis[N];void dfs(int idx){if (l+r>=v){ans=min(ans,abs(l-r));}if (idx>n || ans==0){return ;}for (int i=idx;i<=n;++i){if (!vis[i]){vis[i]=1;l+=a[i],r+=b[i];dfs(i+1);l-=a[i],r-=b[i];vis[i]=0;}}
}signed main(){cin>>n>>v; 	//v是最大的好感度for (int i=1;i<=n;++i){cin>>a[i]>>b[i];} dfs(1);if (ans==INF) cout<<-1;else cout<<ans;
}

医院设置https://www.luogu.com.cn/problem/P1364

题目描述

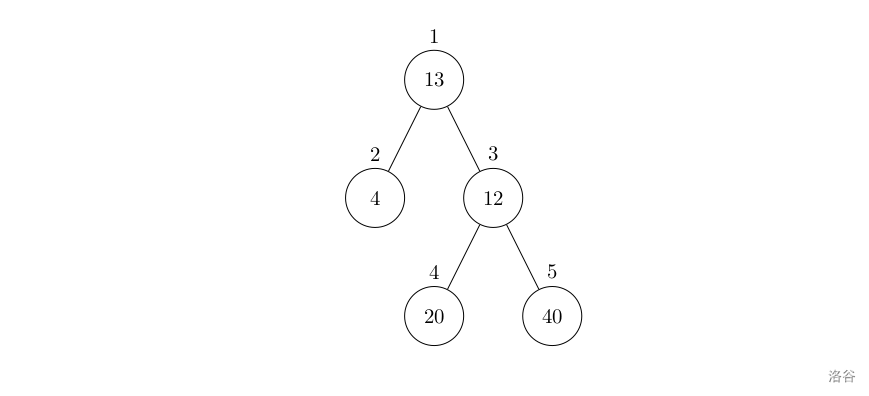
设有一棵二叉树，如图：

其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 11。如上图中，若医院建在 11 处，则距离和 =4+12+2×20+2×40=136=4+12+2×20+2×40=136；若医院建在 33 处，则距离和 =4×2+13+20+40=81=4×2+13+20+40=81。

输入格式

第一行一个整数 �n，表示树的结点数。

接下来的 �n 行每行描述了一个结点的状况，包含三个整数 �,�,�w,u,v，其中 �w 为居民人口数，�u 为左链接（为 00 表示无链接），�v 为右链接（为 00 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1复制

5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1复制

81

说明/提示

数据规模与约定

对于 100%100% 的数据，保证 1≤�≤1001≤n≤100，0≤�,�≤�0≤u,v≤n，1≤�≤1051≤w≤105。

思路：n<=100数据量小，可以用floyd算法，找到最短路径，然后根据权，再遍历所有的点找到最适合的点

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3fconst int N=105;int n,a[N][N],w[N];signed main(){cin>>n;for (int i=1;i<=n;++i){for (int j=1;j<=n;++j){if (i==j) a[i][j]=0;else a[i][j]=INF;}}for (int i=1;i<=n;++i){int l,r;cin>>w[i]>>l>>r;if (l>0) a[i][l]=a[l][i]=1;if (r>0) a[i][r]=a[r][i]=1;}for (int k=1;k<=n;++k){for (int i=1;i<=n;++i){for (int j=1;j<=n;++j){a[i][j]=min(a[i][j],a[i][k]+a[k][j]);}}}int sum=INF;for (int i=1;i<=n;++i){int cnt=0;for (int j=1;j<=n;++j){cnt+=a[i][j]*w[j];	}sum=min(sum,cnt);}cout<<sum;
}