算法学习——LeetCode力扣贪心篇1

在这里插入图片描述

455. 分发饼干

455. 分发饼干 - 力扣（LeetCode）

描述

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示

1 <= g.length <= 3 * 104
0 <= s.length <= 3 * 104
1 <= g[i], s[j] <= 231 - 1

代码解析

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int num = 0 , s_point = s.size()-1;//饼干和孩子排序sort(g.begin() , g.end());sort(s.begin() , s.end());//先用最大的饼干开始喂能吃饱的孩子，吃不饱的跳过不喂for(int i=g.size()-1 ; i >= 0 && s_point >=0 ;i--){if( s[s_point] >= g[i]){s_point--; //喂好一个饼干指针减少num++;}}return num;}
};

376. 摆动序列

376. 摆动序列 - 力扣（LeetCode）

描述

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个摆动序列，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为摆动序列的最长子序列的长度。

示例

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

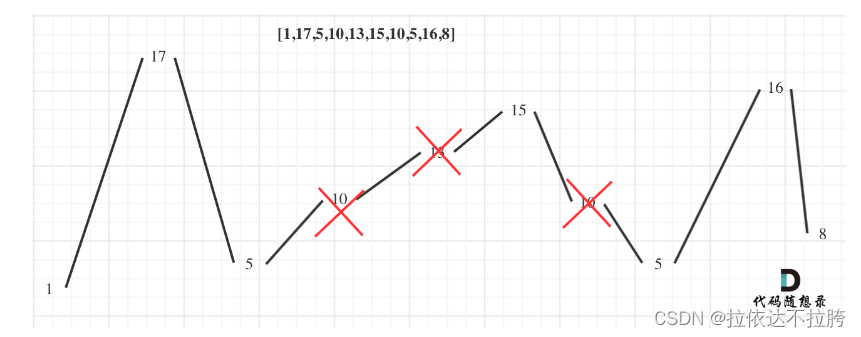
输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

提示

1 <= nums.length <= 1000
0 <= nums[i] <= 1000

进阶

你能否用 O(n) 时间复杂度完成此题?

代码解析

贪心法

核心思想是找山坡。接替找上山坡和下山坡
在开始由前两个点确定向上还是向下
开始向上，就找向下
开始向下就找向上

在这里插入图片描述

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size()==1 ||(nums.size()==2 && nums[0] != nums[1]) ) return nums.size();int pre = 0 ,num = 0 ; bool flag ,start = false ;for(int i=1 ，pre = 0; i<nums.size() ;i++ , pre++) //遍历所有点，pre是前一个点，i是当前点{if(nums[i] == nums[pre]) continue; //如果遇到相同点跳过if(start == false)//start是开始标志，当第一次开始时，确定第一个坡是上山还是下山{if (nums[i] > nums[pre] ) flag = 0; //第一个坡是上山，flag为0，找下山坡else flag = 1;                      //第一个坡是下山，flag为1，找上山坡start = true;  //开始正式循环找num++;//第一个坡记录}else if(start == true){if(   (flag == 1 && (nums[i] > nums[pre]))      //上一个是下坡，找到上坡了||(flag == 0 && (nums[i] < nums[pre]))    ) //上一个是上坡，找到下坡了{num++; //记录坡数flag = !flag;//标志反转，找完上接着下，进行摆动}  }}//num是坡的数量，第一个坡是俩点，补上第一个点+1return num+1;}
};

dp法

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size()==1) return 1;vector<int> dp(nums.size(),1);int flag = -1;for(int i=1 ; i<nums.size();i++){if(flag==-1){if(nums[i]-nums[i-1] > 0) {flag=1;dp[i] = dp[i-1] +1;}else if(nums[i]-nums[i-1] < 0){flag=0;dp[i] = dp[i-1] +1;} continue;}if(nums[i]-nums[i-1] > 0 && flag==0 ){dp[i] = dp[i-1] + 1;flag = 1;}else if(nums[i]-nums[i-1] < 0 && flag==1){dp[i] = dp[i-1] + 1;flag = 0;}else{dp[i]=dp[i-1];continue;}// cout<<dp[i]<<" ";}return dp[nums.size()-1];}
};

53. 最大子数组和

53. 最大子数组和 - 力扣（LeetCode）

描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示

1 <= nums.length <= 105
-104 <= nums[i] <= 104

进阶

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

代码解析

贪心法

class Solution {
public:int maxSubArray(vector<int>& nums) {int sum=0 ,result= INT32_MIN;      //sum是当前数组的和，result是sum中最大的时候for(int i=0 ; i<nums.size() ;i++){sum += nums[i];  //记录当前的sumif(sum > result) result= sum;  //如果sum大于当前result，更新resultif(sum < 0) sum = 0;  //某一个时期的sum小于0舍去}return result;}
};

动态规划

class Solution {
public:int maxSubArray(vector<int>& nums) {vector<int>  dp(nums.size() ,0);int result = INT_MIN;dp[0]= nums[0];for(int i=1 ; i<nums.size() ;i++){dp[i] = max(nums[i],dp[i-1]+nums[i]);}for(int i=0 ; i<nums.size() ;i++) {// cout<<dp[i]<<' ';if(dp[i] > result) result = dp[i];}return result;}
};

122. 买卖股票的最佳时机 II

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

描述

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在同一天出售。

返回你能获得的最大利润。

示例

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示

1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

代码解析

贪心算法

核心思想是找到利润。然后利润大于0的相加

class Solution {
public:int maxProfit(vector<int>& prices) {vector<int> profit; int result = 0;for(int i=1 ;i < prices.size(); i++){if(prices[i] - prices[i-1] > 0 ) //单日利润大于0的存入profit.push_back(prices[i] - prices[i-1]);}for(int i=0 ; i < profit.size(); i++) //计算利润和result += profit[i]; return result;}
};

动态规划

dp数组的含义：

dp[i][0] 表示第i天持有股票所得现金。
dp[i][1] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][0]

第i-1天就持有股票，那么就保持现状，即：dp[i - 1][0]
第i天买入股票，就是昨天不持有股票的所得现金减去今天的股票价格
即：dp[i - 1][1] - prices[i]

]如果第i天不持有股票即dp[i][1]的情况

第i-1天就不持有股票，那么就保持现状，即：dp[i - 1][1]
第i天卖出股票，所得现金就是按照今天股票佳价格卖出后所得现金
即：prices[i] + dp[i - 1][0]

class Solution {
public:int maxProfit(vector<int>& prices) {if(prices.size()<=1) return 0;vector<vector<int>> dp(prices.size() , vector<int>( 2,0 ) );dp[0][0] = -prices[0];dp[0][1] = 0;for(int i=1 ; i<prices.size() ;i++){dp[i][0] = max( dp[i-1][0] , dp[i-1][1] - prices[i] );dp[i][1] = max( dp[i-1][1] , dp[i-1][0] + prices[i] );}return  dp[prices.size()-1][1];}
};

55. 跳跃游戏

55. 跳跃游戏 - 力扣（LeetCode）

描述

给你一个非负整数数组 nums ，你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ，所以永远不可能到达最后一个下标。

提示

1 <= nums.length <= 104
0 <= nums[i] <= 105

代码解析

回溯法（超时）

class Solution {
public:bool backtraking(vector<int>& nums  , int target ,int step){if (step == target) return 1; //检验步子能否到达最后点else if (step > target) return 0;if(nums[step]==0) return 0;for(int j=nums[step] ; j >= 1; j--){if(backtraking(nums ,target , step + j )) return 1; }return 0;}bool canJump(vector<int>& nums) {int target = nums.size() - 1;int step = 0;return backtraking(nums,target,step);}
};

贪心

class Solution {
public:bool canJump(vector<int>& nums) {int cover=0;for(int i=0 ; i<nums.size()-1 && i <= cover ; i++) //循环点，保证点是覆盖范围内的{if(i+nums[i] > cover ) cover = i+nums[i]; //如果当前点的范围大于现在范围，范围更新}if(cover >= nums.size()-1) return 1;   //如果范围覆盖最后一个点返回成功else return 0;}
};