今日复习计划:DFS搜索基础
1.简介
搜索方法:穷举问题解空间部分(所有情况),从而求出问题的解。
深度优先搜索:本质上是暴力枚举
深度优先:尽可能一条路走到底,走不了再回退。
2.DFS和n重循环
给定一个数字x,将其拆分成3个正整数,后一个要求大于等于前一个,给出方案。
最简单的思想:三重循环暴力求解。
若是拆分成n个正整数,就需要实现n重循环
n重循环 = 特定的树状结构 = DFS搜索
举个例子:
给定一个数字6,将其 拆分成3个正整数,后一个要求大于等于前一个,给出方案。
将其拆分成3个正整数,当然需要3重循环
第一层:0
第二层:1 2 3 4 5 6
第三层:6组1 2 3 4 5 6,分别连接第二层的每个数字
这就是我们上数学时经常画的树状结构图。
n重循环,同样的道理
给定一个数字x,将其 拆分成n个正整数,后一个要求大于等于前一个,给出方案。
需要n重循环,也就是需要n层树状结构
用DFS:从上往下找一条合法的路径,所谓合法,就是要满足路径值不递减,长度为n,和为x三个条件。
我来把它转化成代码:
def dfs(depth):# depth:表示当前处于第depth层# 递归出口if depth == n:# 判断数字是否递增for i in range(1,n):if path[i] >= path[i - 1]:continueelse:returnif sum(path) != x:return# 这才是我们要的答案print(path)return# 对于每一层,枚举当前拆出的数字for i in range(1,x + 1):path[depth] = i # 当前层拆出了一个i,记录上去dfs(depth + 1)x = int(input()) # 题目给的数字
n = int(input()) # 需要拆分成n重循环
# path = [i] # 表示第i个数字,给path一个初始值
path = [0] * n
dfs(0)运行结果:
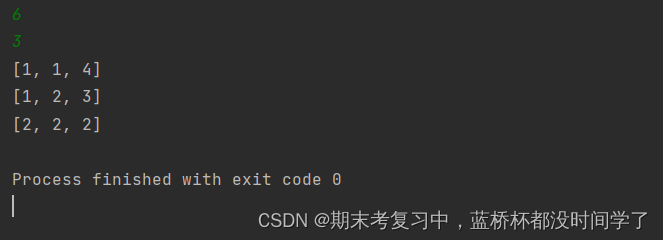
当然了,可以优化:
def dfs(depth,last_value):# depth:表示当前处于第depth层# 递归出口if depth == n:if sum(path) != x:return# 这才是我们要的答案print(path)return# 对于每一层,枚举当前拆出的数字for i in range(last_value,x + 1):path[depth] = i # 当前层拆出了一个i,记录上去dfs(depth + 1,i)x = int(input('输入题中的数字:')) # 题目给的数字
n = int(input('请输入题目要求要拆分成几重循环:')) # 需要拆分成n重循环
# path = [i] # 表示第i个数字,给path一个初始值
path = [0] * n
dfs(0,0)
运行结果:
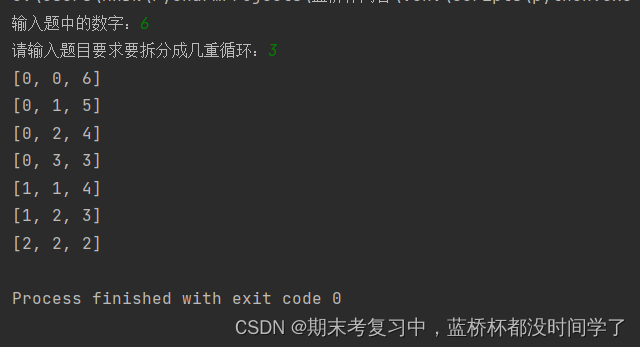
这里的区别是:(我举个例子)
给定一个数字6,将其 拆分成3个正整数,后一个要求大于等于前一个,给出方案。
将其拆分成3个正整数,当然需要3重循环
第一重:0
第二重:1 2 3 4 5 6
第三重:1 2 3 4 5 6(对应数字1) 2 3 4 5 6(对应数字2)3 4 5 6(对应数字3)
4 5 6(对应数字4)5 6(对应数字5)6(对应6)
就是把不必要的分支去掉了,类似于《运筹学》中“分支定界法”的“减支”这一步骤
例题1:分糖果
题目描述:
两种糖果分别于9个和16个,,要全部分给7个小朋友,每个小朋友得到的糖果总数最少为2个最多为5个,问有多少种不同的分法,且糖果必须全部分完。
只要有其中一个小朋友在两种方案中分到的糖果不完全相同,这两种方案就算两种不同的方案。
答案提交:
这是一道结果填空的题,你只需要算出结果都提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
用7重循环,每重循环代表一个小朋友,每个小朋友枚举自己的糖果情况。
参考答案:
ans = 0
def dfs(depth,n,m):# depth:第depth个小朋友# n:第一种糖果的剩余量# m:第二种糖果的剩余量# 递归出口if depth == 7:if n == 0 and m == 0:global ansans += 1return# 接下来枚举每个小朋友的情况# 第一种糖果的情况for i in range(0,6):# 因为每个人最多5个糖果# 第二种糖果的情况for j in range(0,6):# 接下来是题目所给的条件if 2 <= i + j <= 5 and i <= n and j <= m:dfs(depth + 1,n - i,m - j)dfs(0,9,16) # 这是题目给的初始值
print(ans)
运行结果:
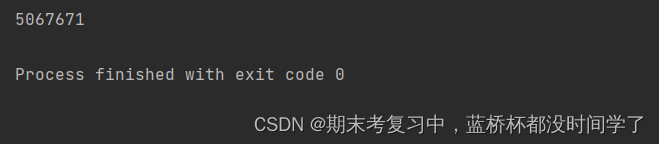
例题2:买瓜
题目描述:
小蓝正在一个瓜摊上买瓜,瓜摊上共有n个瓜,每个瓜的质量为Ai。
小蓝刀工了得,他可以把任何瓜劈成等重的两份,不过每个瓜只能劈一刀,小蓝希望买到的瓜的重量的和恰为m。
请问小蓝至少要劈多少个瓜才能买到质量恰好为m的瓜。
如果怎样小蓝都无法得到总重恰好为m的瓜,请输出-1。
输入描述:
输入的第一行包含两个整数n,m,用一个空格分开,分别表示瓜的个数和小蓝想买到的瓜的总重量。
第二行包括n个整数Ai,相邻整数之间用空格分隔,分别表示每个瓜的重量。
输出描述:
输出一个整数,表示答案。
思路:
n重循环,每重循环3种情况:买一个,买一半,不买。
参考答案:
def dfs(depth,weight,cnt):if weight > m:returnif weight == m:global ansans = min(ans, cnt)if depth == n:return# 枚举当前3种情况dfs(depth + 1,weight + 0,cnt)dfs(depth + 1,weight + A[depth],cnt)dfs(depth + 1,weight + A[depth] // 2,cnt + 1)n,m = map(int,input().split())
m *= 2
A = list(map(int,input().split()))
A = [x * 2 for x in A]
ans = n + 1
dfs(0,0,0)
if ans == n + 1:ans = -1print(ans)运行结果:
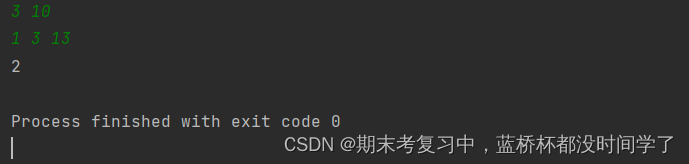
OK,这篇就先写到这里,下次继续!
(若有不懂的地方,可以互相交流)
)


)
)
)

)









)

