学了常见的筛法,让我们看个题:

首先,我们知道欧拉筛复杂度为nlognlogn,这题可以承受,但是空间上存不了,而如果我们枚举1--n^1/2,复杂度不允许。
其实在枚举的方法中,我们只需找出有无在【2,n^1/2]的素数即可。
这样,我们就可以用类似打表的形式记入素数。n^1/2差不多3万,有前面的定理可知质数数量差不多几十个,这样子就可以了。
下面介绍算数基本定理:
任何一个N=p1^c1*p2^c2*p3^c3*...(唯一)
推论:N的正约数合集为p1^b1*p2^b2*p3^b3(0<=bi<=ci)
N的正约数的个数为
N的正约数的和为
下面是最大公约数与最小公倍数

下面我们介绍欧拉函数:

我们来看看他们的应用吧:
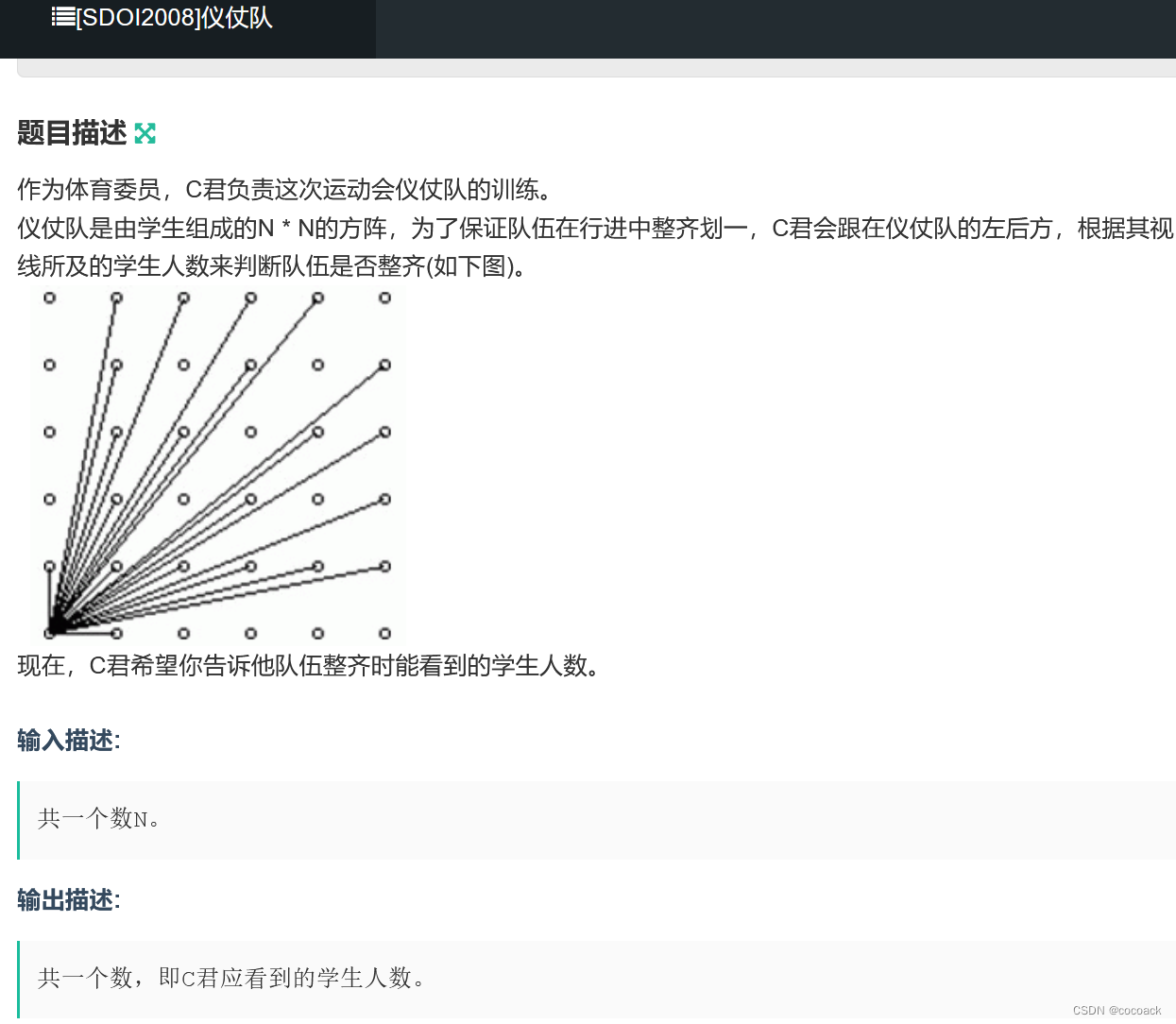
显然,他可以看到横坐标与纵坐标互质的人,我们以y=x分两半,因此,问题等价于求1---n的欧拉函数(注意(1,0),(0,1))
下面因为积性函数,我们可以用筛法求:
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,v[40011],pi[40011],cnt,prime[40011];
long long ans;
int main(){cin>>n;n--;for(int i=2;i<=n;i++){if(v[i]==0){v[i]=i;pi[i]=i-1;prime[++cnt]=i;}for(int j=1;j<=cnt;j++){if(v[i]<prime[j]) break;if(prime[j]*i>n) break;if(prime[j]==v[i]) pi[prime[j]*i]=pi[i]*v[i];else pi[prime[j]*i]=pi[i]*pi[prime[j]];v[prime[j]*i]=prime[j];}ans+=pi[i];}cout<<2*ans+3;
}注意,当prime[j]<v[i]时,这两个互质,可以用积性函数的性质。
当相等时,我们需要用到定义:
i*v[i]他的质因数的种类没变,只要N变成N*v[i]即可。
接题:
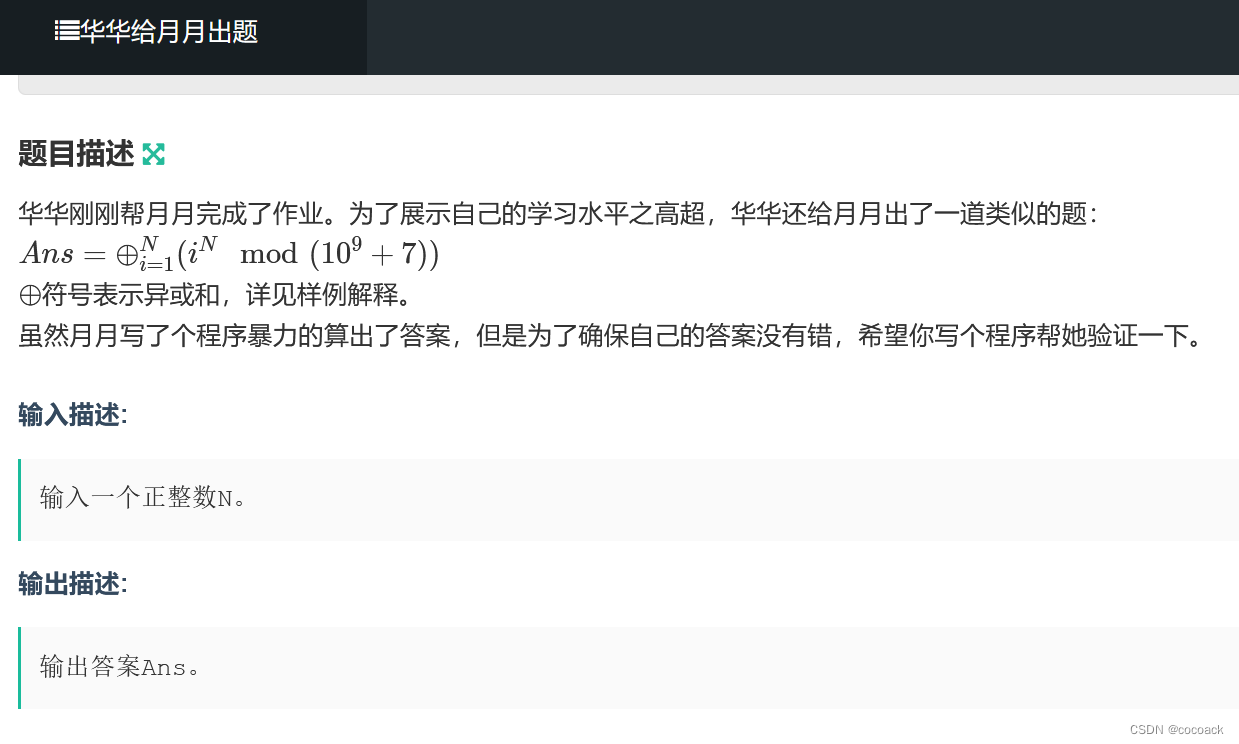
对全部数快速幂会超,我们发现a^n*d^n=(a*d)^n,于是我们配合筛法即可。
下面为AC代码(注意,因为空间的要求,我们把int换成bool ):
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 13e6 + 10;
const int mod = 1e9 + 7;
int n,prime[10000],ans,cnt,pi[maxn];
bool v[maxn];
long long quickmi(long long x,long long b){long long i=1;while(b){if(b&1) i=(x*i)%mod;b>>=1;x=(x*x)%mod;}return i;
}
signed main(){scanf("%d",&n);ans=1;for(int i=2;i<=n;i++){if(v[i]==0){pi[i]=quickmi(i,n);prime[++cnt]=i;}for(int j=1;j<=cnt;j++){if(i%prime[j]==0) break;if(prime[j]*i>n) break;v[prime[j]*i]=1;pi[prime[j]*i]=(pi[prime[j]]*pi[i])%mod;}ans^=pi[i];}printf("%lld",ans);
}




:gem5内存系统——The gem5 Memory System)




)








不支持)