图文并茂讲解Travelling Salesman

题目

思路

一道lca板子题，不会的同学可以先康康详解最近公共祖先(LCA)-CSDN博客

我们可以发现，商人是从1开始，旅行到第一个城镇，再到第二个，第三个……

那么我们只需要求出1~第一个城镇的距离，第一个城镇到第二个城镇的距离，第二个城镇到第三个城镇的距离……最后再把这些距离加起来就得到了答案。

那么，如何求树上两点之间的距离呢?

比如画一张图:

其中deep表示该点的深度(1号节点深度为1)

假设要求u到v之间的距离

那么我们把u到v之间的路径标出来

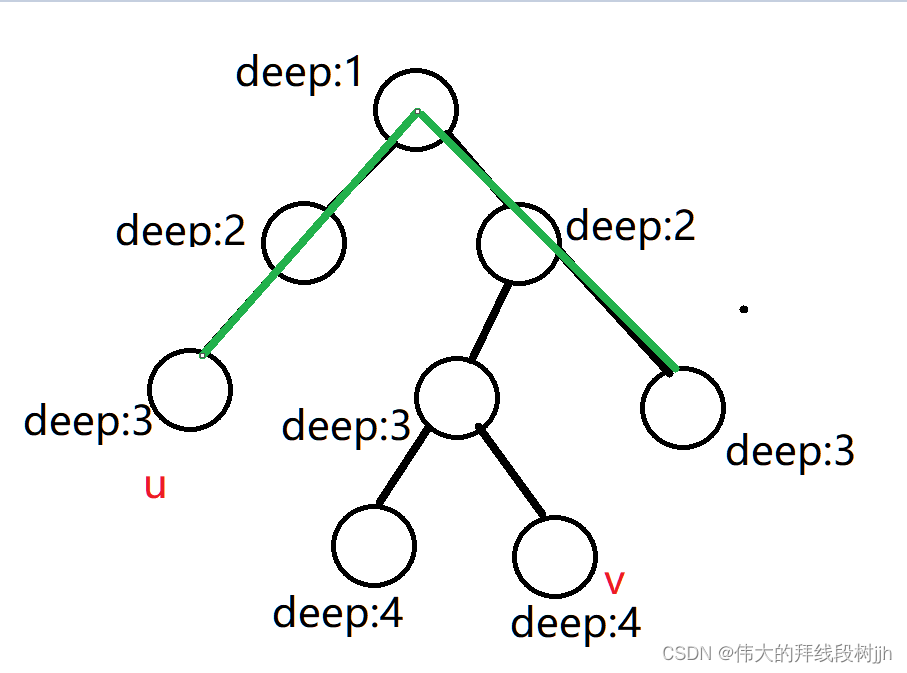我们可以发现u到v之间的最短路径是一定会经过lca(u,v)的。

所以，求u->v之间的距离就转化成了求(u->lca(u,v)之间的距离)+(v->lca(u,v)之间的距离)

那么，u到lca(u,v)之间的距离怎么求呢?

其实就是deep[u] - lca(u,v)!(v同理)

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,mx[300001][41],deep[300001],id = 1,ans,a[1000001];
vector<int> vec[300001];
void dfs(int x,int fa)
{deep[x] = deep[fa] + 1;mx[x][0] = fa;for(int i = 0;i < vec[x].size();i++)if(vec[x][i] != fa)dfs(vec[x][i],x);
}
int lca(int x,int y)
{if(deep[x] < deep[y]) swap(x,y);for(int i = 40;i >= 0;i--)if(deep[mx[x][i]] >= deep[y])x = mx[x][i];if(x == y) return x;for(int i = 40;i >= 0;i--)if(mx[x][i] != mx[y][i]){x = mx[x][i];y = mx[y][i];}return mx[x][0];
}
signed main()
{cin>>n;for(int i = 1;i < n;i++){int u,v;cin>>u>>v;vec[u].push_back(v);vec[v].push_back(u);}dfs(1,0);for(int i = 1;i <= 40;i++)for(int j = 1;j <= n;j++)mx[j][i] = mx[mx[j][i - 1]][i - 1];cin>>m;a[0] = 1;for(int i = 1;i <= m;i++){cin>>a[i];ans += deep[a[i]] + deep[a[i - 1]] - deep[lca(a[i],a[i - 1])] * 2;}cout<<ans;return 0;
}