ONLYOFFICE文档8.0新功能浅探
上个月末这个月初的几天,ONLYOFFICE版本更新了!更新到了一个比较整的大的版本号,8.0版本,看来这个生产力工具的升级速度基本上能保持每年两个版本号的速度,还是很快的,一般来说,能比这种速度还快的,就都是那种纯粹面向消费者的手机端app软件了,它们基本上每年每个重大公农历节庆,都要有更新升级,尤其是春节前的这些天,我手机端的国产app无一例外,打开哪个,都要提醒我它自己要更新了,但是更新内容又不说,哼,别以为我不知道,所有国产手机app春节前更新,都是没有正经功能增加升级的,都是纯而又纯的,增加了很多春节档期的推销广告而已,无一例外,春节大促!

所以我的建议就是,对于个人使用手机端国产app来说,春节前一概拒绝app的更新提示。而对于ONLYOFFICE这样的生产力工具,它的这次更新只是碰巧赶在了临近春节的时候,更新推出的新功能,还是非常有诚意非常提高生产力的。
具体的新功能全面列表的介绍,参见本期推文的第二篇的转载文章吧,它讲解的很全面。而这片文章,略过对咱们没什么用处的新功能,只挑选比较有用的新功能来仔细讲一讲。
ONLYOFFICE这次更新的特点,是三端同更,三端更新的时间非常接近,不像以前那样三端的更新会前后相差很多天。哪三端?ONLYOFFICE作为协作办公软件,大体上有三个地方:一个是咱们个人电脑PC上可以单独的独立安装的本地运行的,处理电脑本地硬盘里文档的个人软件版本,这是Office类软件最早最古老的形式,另一端,是互联网端,Software As Service服务即软件端,由ONLYOFFICE的开发商自己,所提供的在线Office版本,一个团队多个成员可以登上去协作,ONLYOFFICE的服务器端现在主推协作空间这个服务器,以前也有一个叫做工作区的服务器产品,它里面还有什么日历通讯录邮件等功能,但无论是以前的工作区还是现在的协作空间,最基本的功能都是ONLYOFFICE在线文档编辑器功能,第三端,则是自己在互联网上买云主机VPS或者买网络服务器NAS部署在企业内网家庭内网里面,然后在VPS或者NAS上面安装ONLYOFFICE的在线协同办公服务器程序,这种自部署自托管的形式可以参考自己的上一篇图文:
云主机上都可以安装什么有趣的服务 https://blog.csdn.net/VincentYoung/article/details/135828774
https://blog.csdn.net/VincentYoung/article/details/135828774
这次更新,服务器端安装文件已经可以从ONLYOFFICE官网上下载,桌面版如果开启自动更新就会已经自动升级到最新版本了,第二种纯在线SAS的版本直接登上去就已经是最新版本的了,因此,本文所展示的新功能的使用截图,我都是混着用本地版、在线版本的,界面会有细微不同。
表单文件格式从oform转变为pdf

众所周知,ONLYOFFICE之前推出表单格式文件的时候,是用docxf格式来创建编辑表单文件,然后导出oform格式的可填写表单,你也可以再从oform格式导出为pdf格式的可填写表单文件,而现在版本更新到8.0之后,流程简化为了,用docxf格式创建编辑表单文件之后就直接导出pdf格式的可填写表单文件,省略了中间的oform格式文件了。好处就是,pdf格式文件更加的通用常见,几乎所有的电脑即使是初始安装的新电脑,不管是windows操作系统还是linux操作系统,都能直接打开pdf文件,不论是系统自带的pdf阅读器,还是系统自带的网页浏览器,都能打开pdf文件,打开pdf格式的表单就能填写、保存再提交,这可太方便了。
同步的ONLYOFFICE文档8.0版增强了pdf格式文件的支持,例如增加了密码保护的功能:
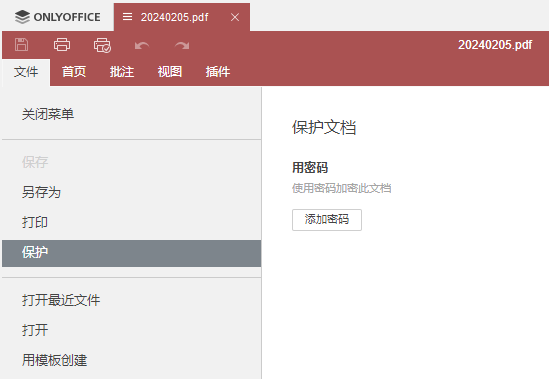
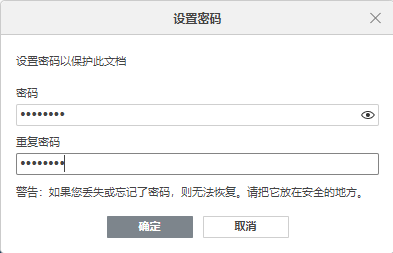
只需要从文件菜单中选择保护,就可以添加密码了
单变量求解
这大概是这次版本更新里面最有用的新增功能之一了,没错,就是单变量求解,字面意思。不懂?就是说,如果您已知公式的结果,但不确定公式所需的输入值,就可以用单变量求解功能从想要的结果反推计算出需要的输入值,就像数学里面的解方程一样,中学数学就学过的,要在表格文件里面使用单变量求解功能,其实很简单,就在菜单栏的数据菜单栏里面,有一个很大的新增加的按钮:单变量求解

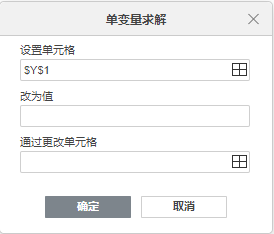
点击即可打开单变量求解对话框
渔
看不懂?授之以鱼不如授之以渔,把单变量求解的问题放一边,我先讲一讲对于这种内涵强大的功能我们去哪里寻找帮助。
不仅仅局限于这一个功能,也不限于ONLYOFFICE这一款软件,即使你用微软Office也不会百分百精通所有功能,总是会遇到知识盲点或者新功能需要学习,这个时候,我们先把软件的语言界面设置为英文,然后再看这个功能英文叫什么:

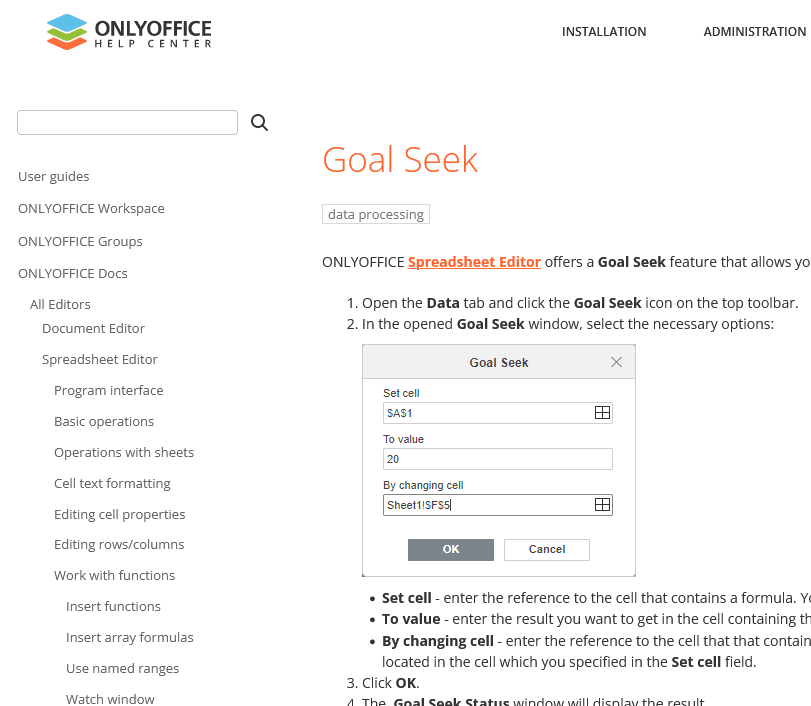
然后到ONLYOFFICE的官方帮助网站和微软Office的官方帮助网站输入这个关键词搜索,就能得道两者关于这个功能的详细讲解了:
goal seek site:onlyoffice.com
到了这里我就已经远远超纲了,所以这里假定各位读者朋友们找不到这个页面,那么微软的不用番羽总还是能找到的
微软的帮助网页就在Use Goal Seek to find the result you want by adjusting an input value这里了,没错,微软Office最大的优势就是,你在任何其它Office里面在功能上有不会的,都可以去微软网站上看帮助细节,准没错的。
解一元一次方程
一般的帮助页面讲这个单变量求解都是拿复利的还贷月供来做例子,但是这是典型的计算机迭代计算,并不太亲民,并不是最简单的例子,最简单的应该是解一元一次方程:
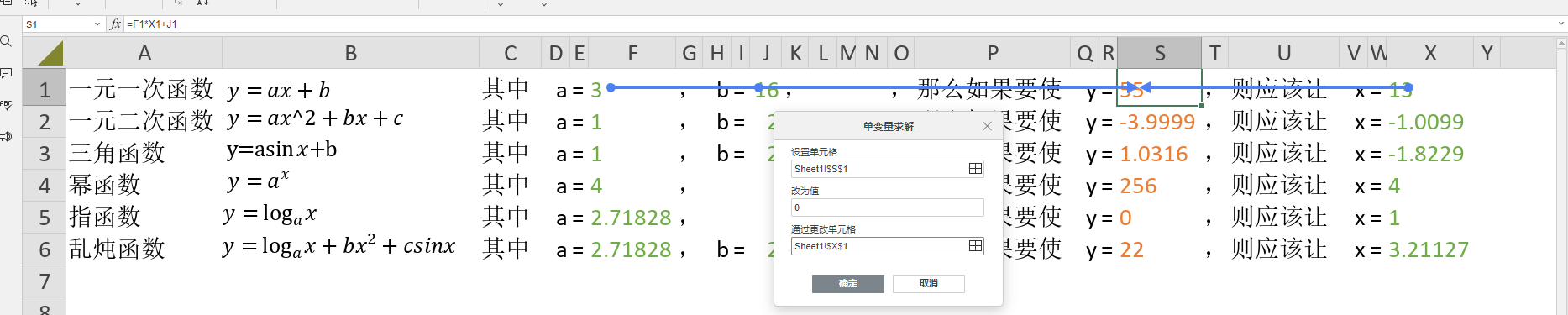
写了一句话,给出了一元一次函数并且用格子给各个参数赋予了数值,然后,如果要使y等于一个数,则应该让自变量等于多少呢?先随便给自变量一个数,然后在函数y的值的格子里面,用表格的公式来把这个一元一次函数表达式写进去计算一下当前我所输入的x的值,所对应的y的值是多少,当然,现在的y值还不是我们要的y值,还仅仅是我们所随便输入的一个x值所得到的y值。
然后,就是用单变量求解器,求解要使y等于几需要x等于几,在这个对话框里面第一个设置项,选中S1格子,就是包含了计算一元一次函数的计算公式的那个格子,而对话框的第二个设置项,输入我们要让这个y最终等于的值,而第三个设置项,就是选择要通过更改哪一个自变量的数值的格子,选择X1格子,就是x,当前y这个公式引用到了3个格子,a、b和x,你也可以把x当作已知数,把a或者b当作自变量未知数来求解,性质是一样的,总之就是求解s1格子所引用到多个格子里面任意指定的一个格子需要取值是多少的这样的操作。三个设置项设置完后点击确定按钮,单变量求解弹出对话框就会变为单变量求解状态弹出框窗口:

一元一次方程做为最简单的数学方程,求解速度也是最快的,几乎是瞬时得到结果,直接点击确定,就可以刷新表格里面的y和x的格子的值了:

求解后y值的S1格子处刷新为0,就是上面在求解对话框中所设置的想要y所得到的值,而x值得X1格子得到了唯一的数值解-5.333333,一看就是无限循环小数了,这并不是一个解析解而是一个数值解,但是一看这个数值你心里面就能看出来解析解是多少了。
为了展示清楚,特意在y值的格子S1上开启了追踪引用单元格的箭头线,用箭头来表示,哪些格子参与计算了哪些格子,也就是哪些格子是自变量可以当作要求姐的未知数,哪个格子是最终变量,非常直观:

解一元二次方程
上面的一元一次方程就仅仅是放一个example而已,实用意义并不大,因为一元一次方程求解太简单了,很多时候甚至都不需要笔算只需要心算就够了,用不到表格来辅助求解,所以这里放两个zample,讲一元二次方程,比上面一元一次方程要优惠了一半,当然了,还不如下面的一元三次便宜…………
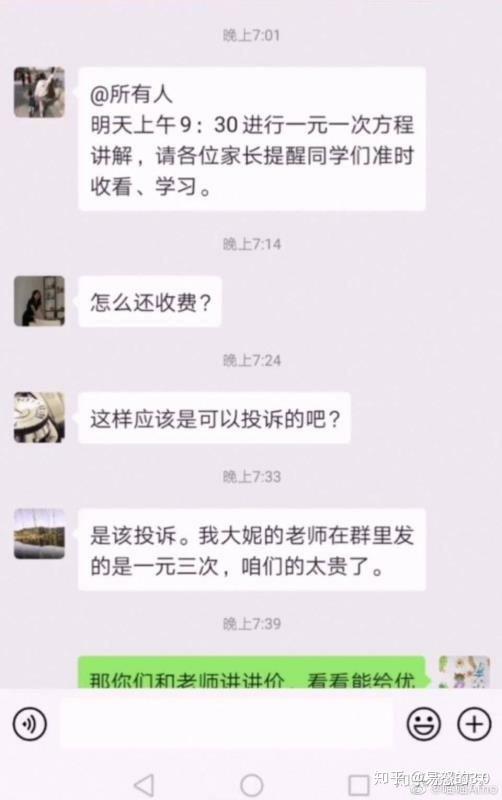
与一元一次方程不同,一元二次方程不一定有解。一元一次方程对应的是xy平面坐标上的任意一条直线,只要它不是水平的,则y的任意值都可以求解到x的唯一解,但是一元二次函数对应的是一条抛物线,对应于一个最终的y值,未知数x可能求得两个解,或者唯一解,或者没有实数解。比如本文的一元二次方程,对应其参数a和b的值,xy抛物线是下图这样的,对了,这个抛物线图也是用ONLYOFFICE的表格编辑器制作的
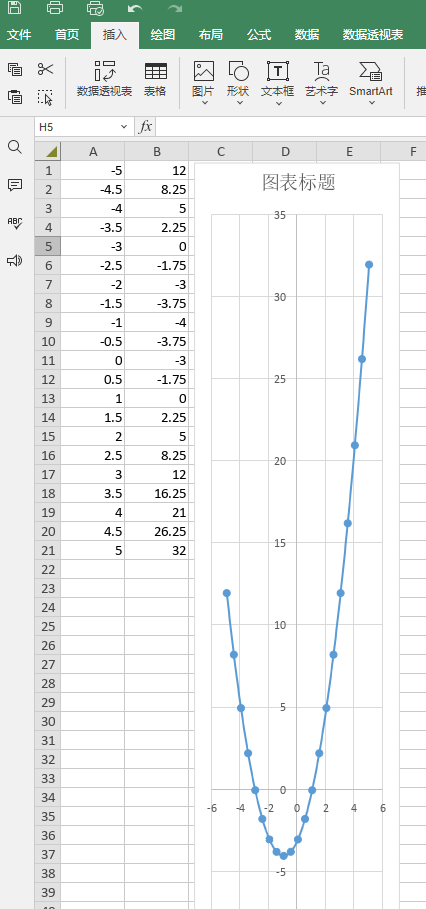
由图上可以直观看出来,x取值-1的时候,函数y得到最小值大概是-4,所以,如果要求这条抛物线在什么地方y的值是-5、-6等更小的数值,那么就会必然求解不出来的,这个单变量求解功能就会报告无解。
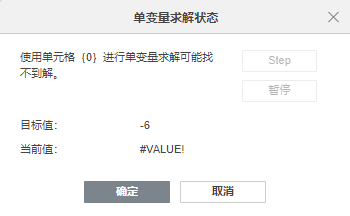
那么问题来了,在非最小值处,一元二次方程都应该是有两个姐的,大姐和二姐,那么,这个单变量求解功能得到的是哪一个解呢?据我的观察,它这个功能似乎大概是求解距离0最近的一个解,它背后底层的算法大概其是从0开始迭代计算的,直到求解得到一个解,就返回,不再寻找是否还存在其它解。
三角函数
比两个解更多的是,周期性存在无数个解的,三角函数方程。
![]()
上面的一元一次方程和一元二次方程,徒手计算都能得到解析解和数值解,非常简单,而这个三角函数,徒手计算就只能得到解析解,要想得到数值解,那就必须拿一本数学用表在里面查阅正弦数值表了,或者拿个科学型计算器来按出来,三角函数方程求数值解就不是徒手能计算出来的了。

这种不能徒手计算出来的数值解的方程,就能体现出ONLYOFFICE表格编辑器里面的单变量求解的实际作用来了,虽然只能求出多个解之中的一个接来,但是我们熟悉三角函数的都知道,其余的解,都是周期性的,每一个周期里面两个解,两个解是在波峰或波谷左右两侧对称分布的,这样我们就能继续了,从这一个解来找出其余的解了,如下图所示
图表向导新功能
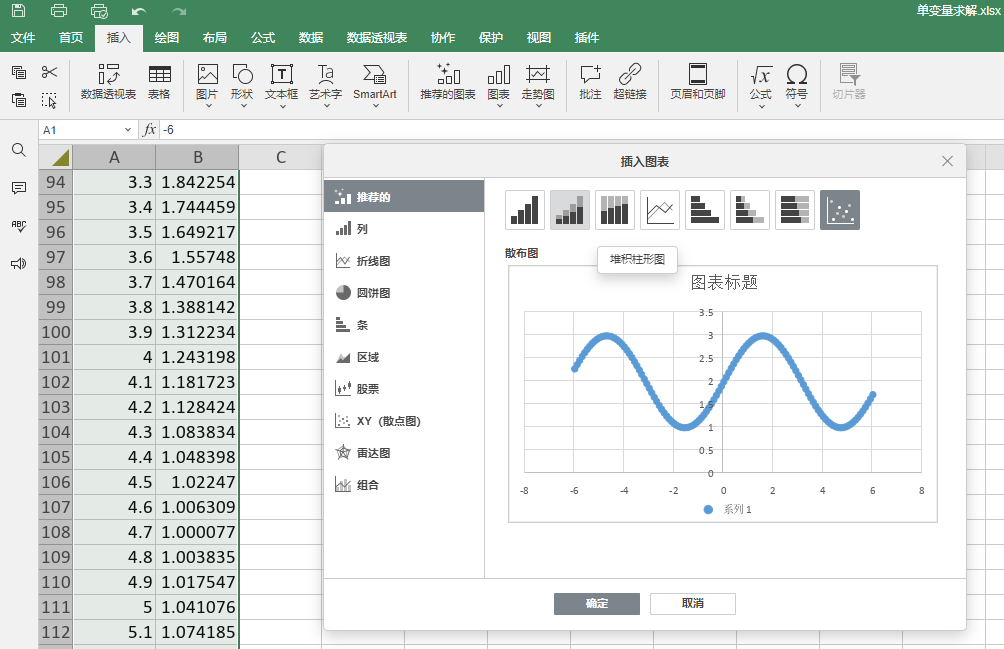
如上图所示,本次ONLYOFFICE版本升级新增的一个功能就是图表向导,它会自动的根据你所选择的数据范围内的数据来比较聪明的推荐适合于该数据的图表,只需要在插入菜单里面选择“推荐的图表”大按钮,就会在插入图表对话框中首先推荐一排图表类型,这里我选择推荐的最右侧的散步图类型。
幂函数指函数

类似的,解析解可以徒手算出来,数值解必须借助数学用表或计算器的,幂函数、指函数、对数函数等构造的一元方程
都可以用单变量求解功能来求解,这个功能并不仅仅针对一次、二次、三次等普通的方程可以用,对任何类型的函数构成的方程,只要是一元的,都能求解,真的很良心,绝不收二元、三元更贵的价格,只要一元!你买不了上当,买不了吃亏,只需要一元!能解一切的一元方程!
乱炖函数
单变量求解功能有多强大呢?你可以乱炖函数创建复杂的一元方程,让它去解!上面的不管是一次方程还是二次方程,都是有求解公式的,也就是说,不用单变量求解功能,也可以直接在表格编辑器中手写求解公式来直接计算数值解,只要你的数学技能足够强,但是现实中,并不是所有数学方程都能推导出求解公式的,就只能用计算机一元求解算法来暴力求解,这才是单变量求解功能的用处:

这是自己随便编的一个乱炖函数,什么奇怪东西都有,我甚至无法徒手在纸上计算推导它最后是否有解,有几个解,解析解是多少,数值解更是无从计算,我只能大概手绘这个函数的曲线的大概形状来判断它的解的分布,那么这就可以让单变量求解功能来大显身手了
实例之某反省野国师笑话
键政专家的博客每多一个数学物理公式都会掉粉多少个,上面这么多公式看起来太讨厌了,所以这里自己再举一个例子,咱们野生国师键盘政军家最爱的


关于反导拦截的一个经典笑话:

正确的计算公式应该是这样的,如下截图所示各个格子
=(1-POWER((1-B1),G2))
现实中,真正的问题其实是这样问的,我一枚导弹的拦截命中成功率是已知的,那么为了成功拦截,我一次齐射两枚或者三枚或者更多,使得其中至少有一枚能够命中拦截来袭导弹的概率,能够达到一个很高的数值,比如百分之九十九,那么,我究竟需要一次齐射多少枚地空拦截弹?
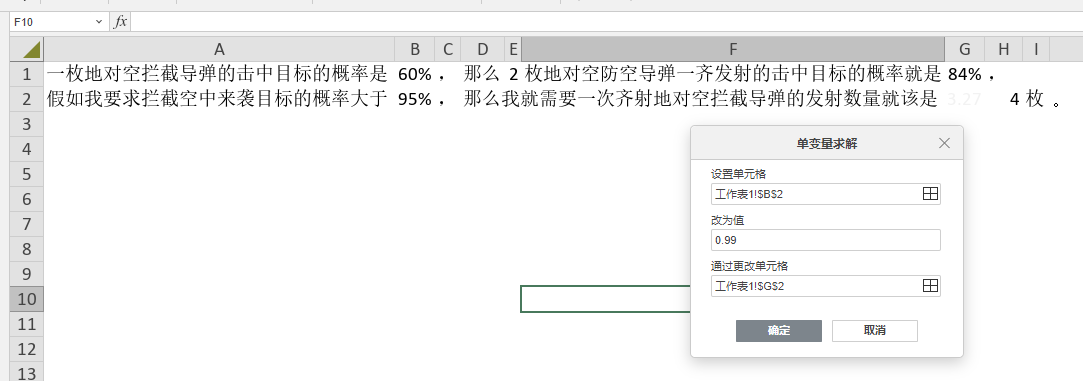
这里需要注意的是概率的输入必须是小数的形式,99%的概率要输入为0.99,求解得到的数值解是有小数部分的,并不能直接四舍五入,比如得到的答案是5.03枚,那就是必须得齐射6枚才行,得也就是要使用ceiling函数处理一下求解结果

颜色动态变化动画效果
在之前的图文中自己介绍过可以用幻灯片切换页面的变形效果来实现颜色动态变化的动画
// 插入图文链接
但是这必须做成多个幻灯片页面来做,稍微麻烦一些,而这一次升级到8.0版本后,则可以直接针对任何图形元素本身施加变色动画功能了:
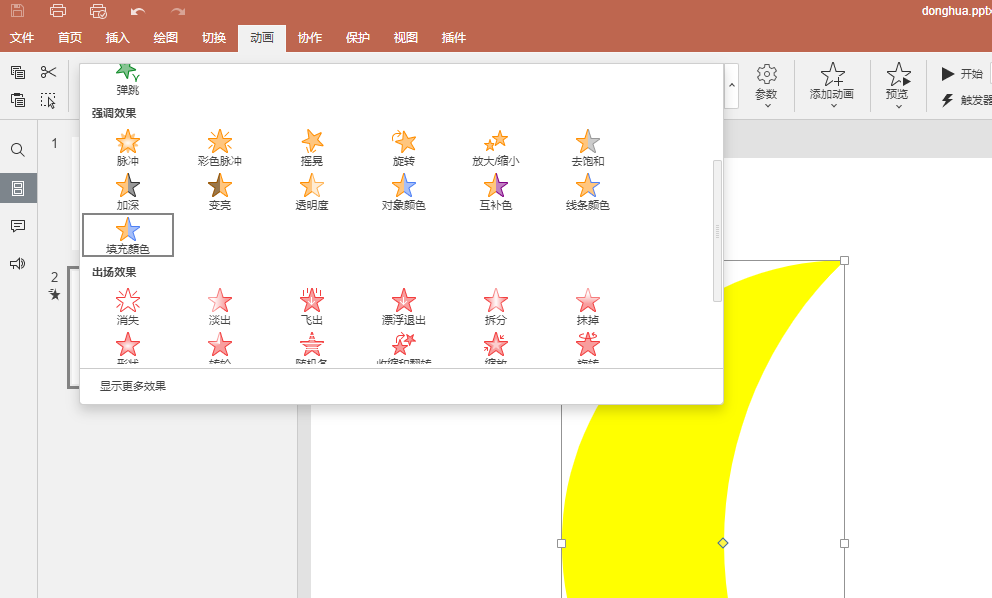
只需要选中一个图形对象,然后在动画菜单栏内,从强调效果类型中,选择最后一个“填充颜色”,即可,
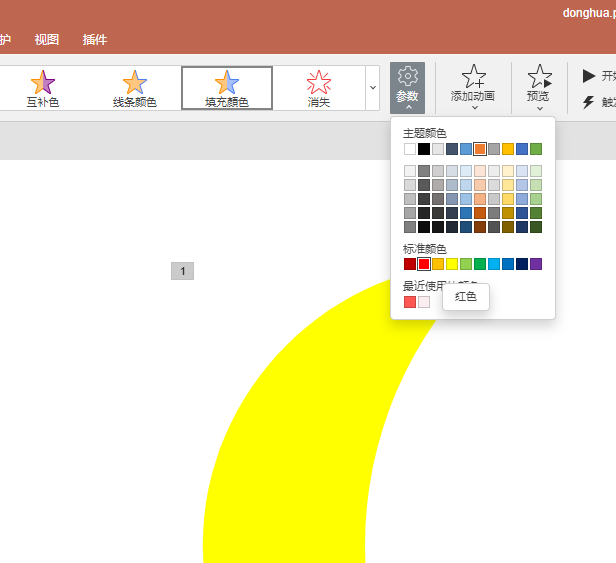
然后在右侧的参数下拉按钮中选择要变化到的颜色,比如,从正常的金色月亮变成血红的红月:

插件界面可视化的更新
这次更新后,终于可以同时启用多个插件功能了,开启多个插件后,会在左侧工具栏上显示多个插件的按钮,就可以切换多个插件的插件栏来用了,并且,最关键的是之前的左侧工具栏的宽窄无法鼠标拖动调节,这次更新,我终于可以随意调节了,这样终于可以下面的聊天窗口拉宽了看梗图了,新色魔团伙BBS的娇客版关了后自己就只剩下这一个地方看笑话了:

当然也有的插件本来就不是在左侧工具栏使用的,比如ChatGPT插件,就是主要通过弹出式Popup窗口来使用的:

安装过人工智能ChatGPT插件的朋友们可能会发现,这次更新后,插件菜单栏内的ChatGPT按钮好像不见了,怎么找回来呢?现在ONLYOFFICE里面可以手动更新各个不同的插件了:
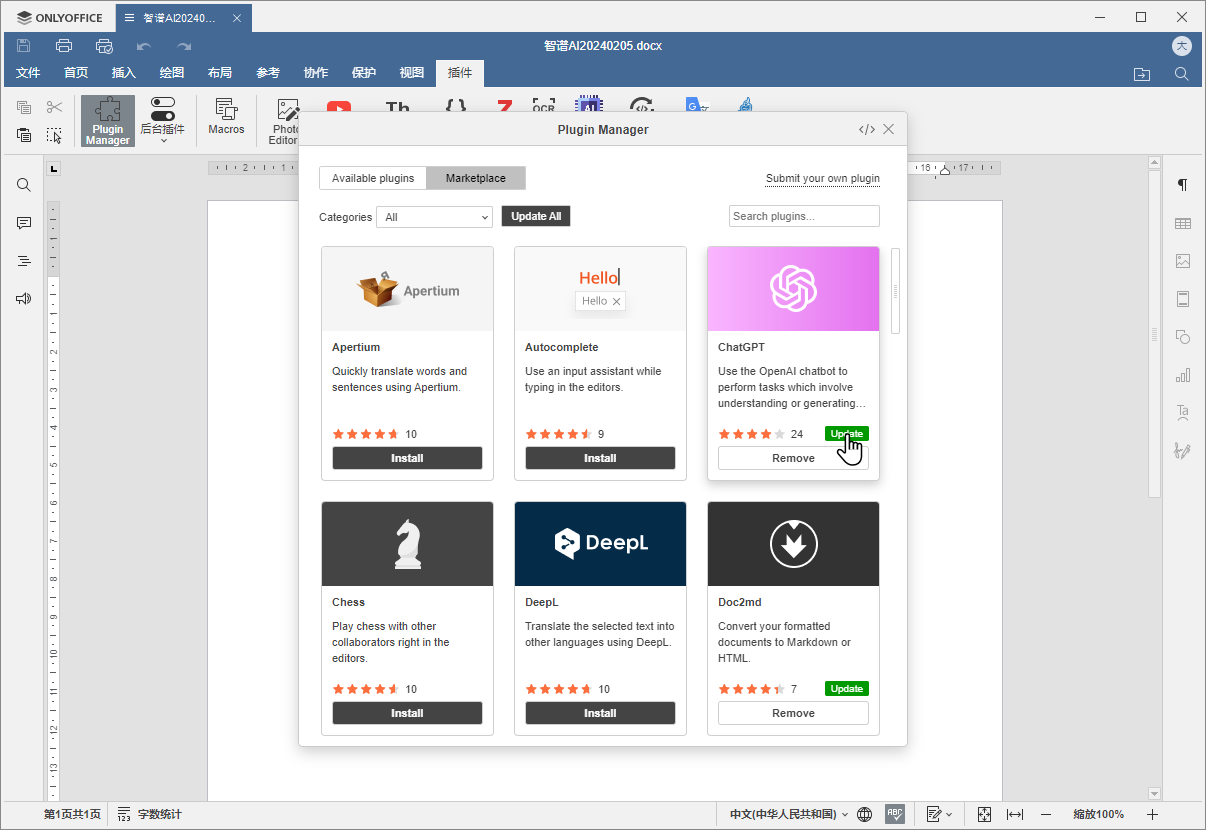
只需要打开插件管理器,就可以看到ChatGPT插件还在,点击更新按钮。

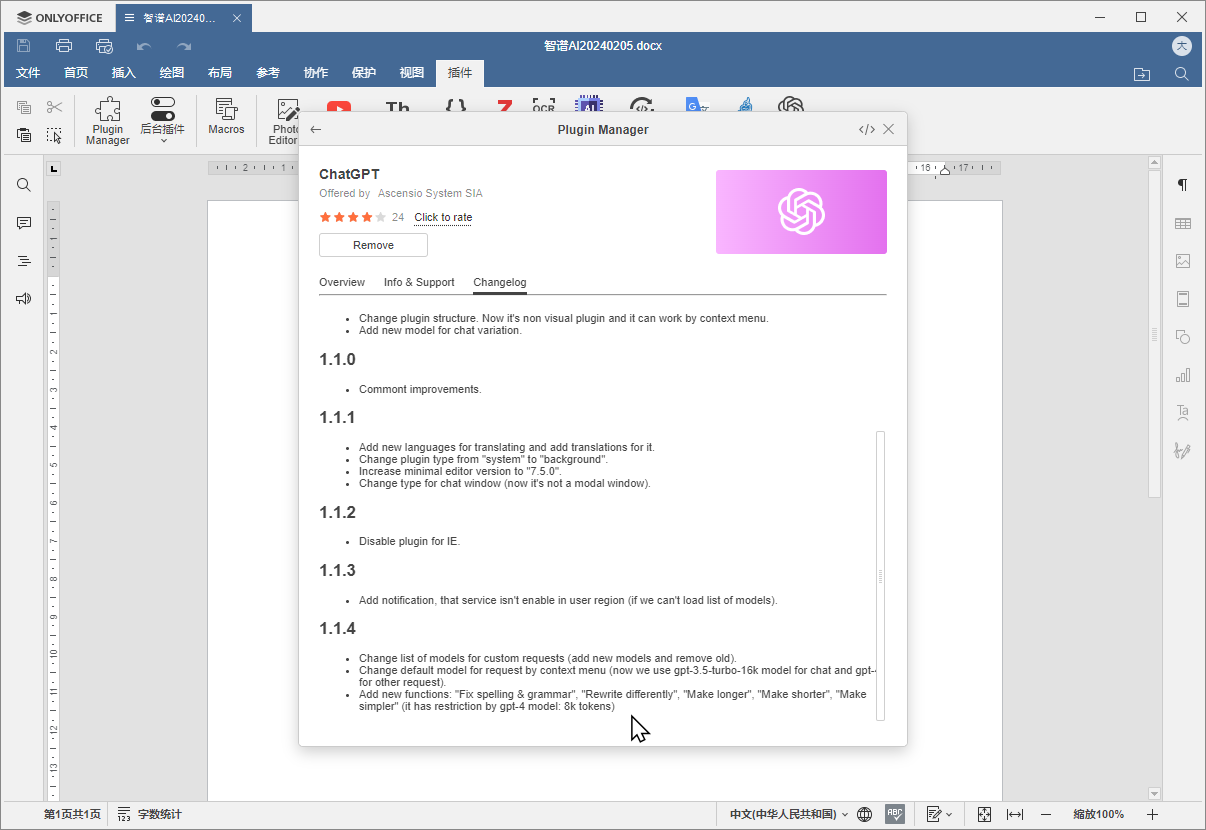
确认更新,就可以针对单独的一个一个插件来更新插件的版本了,可以切换到changeslog页面查看插件自己的更新记录版本新特性:
其它功能
为什么要略去,比如Right to Left从右向左的界面功能,这是为了适应中东骆驼文那种从右向左文字而推出的功能,咱们用不上,万一设置切换过去RTL了,再想切换回来你可能都眼花找不回来,就像一个赛博灯泡一样,千万不要好奇而尝试!
还有新增了可以自定义头像、显示头像的功能,在网络协作的时候,看对方的图标不再是名字的首字母缩写了:
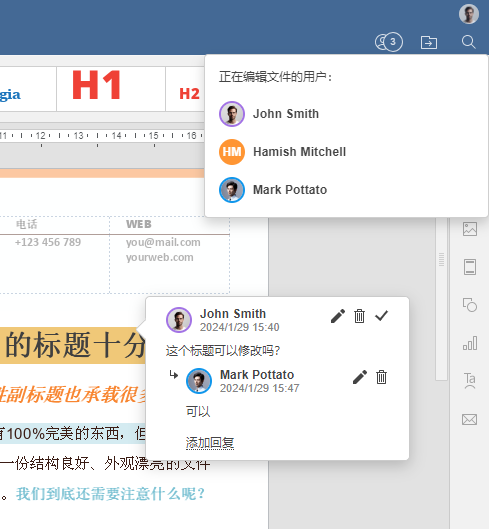
但是我希望你们在协作办公中千万不要遇上我这样的换头像换昵称狂魔协作杀手
参考文献
ONLYOFFICE 文档 8.0 现已发布:PDF 表单、RTL、单变量求解、图表向导、插件界面设计等更新
Goal Seek
一元一次方程是什么梗???
什么是科学计算器
台湾省1发“天弓”成功率“70%”,3发真能210%拦截大陆导弹?反导拦截难在哪里?



)
-HPA实战)



)



)






