Think-on-Graph:解决大模型在医疗、法律、金融等垂直领域的幻觉
- Think-on-Graph 原理
- ToG 算法步骤:想想再查,查查再想
- 实验结果
论文:https://arxiv.org/abs/2307.07697
代码:https://github.com/IDEA-FinAI/ToG
Think-on-Graph 原理
幻觉是什么:大模型的「幻觉」问题。
-
多跳推理路径的探索算法,提高深度推理能力:ToG 通过在知识图谱中动态探索多个推理路径,并利用 beam search 算法挑选最有前景的路径,从而增强了LLMs的深度推理能力。
-
显式、可编辑的推理路径,增强推理的责任感和可追溯性:通过提供明确的推理路径,ToG不仅增加了推理过程的可解释性,而且允许对模型输出的来源进行追踪和校正,从而提高了推理的责任感和可靠性。
-
插件式框架,提高大模型的灵活性和效率:通过知识图谱而非LLMs更新知识,可以提高知识的更新频率,降低更新成本,同时增强小型LLMs的推理能力,使其能与大型模型(如GPT-4)竞争。
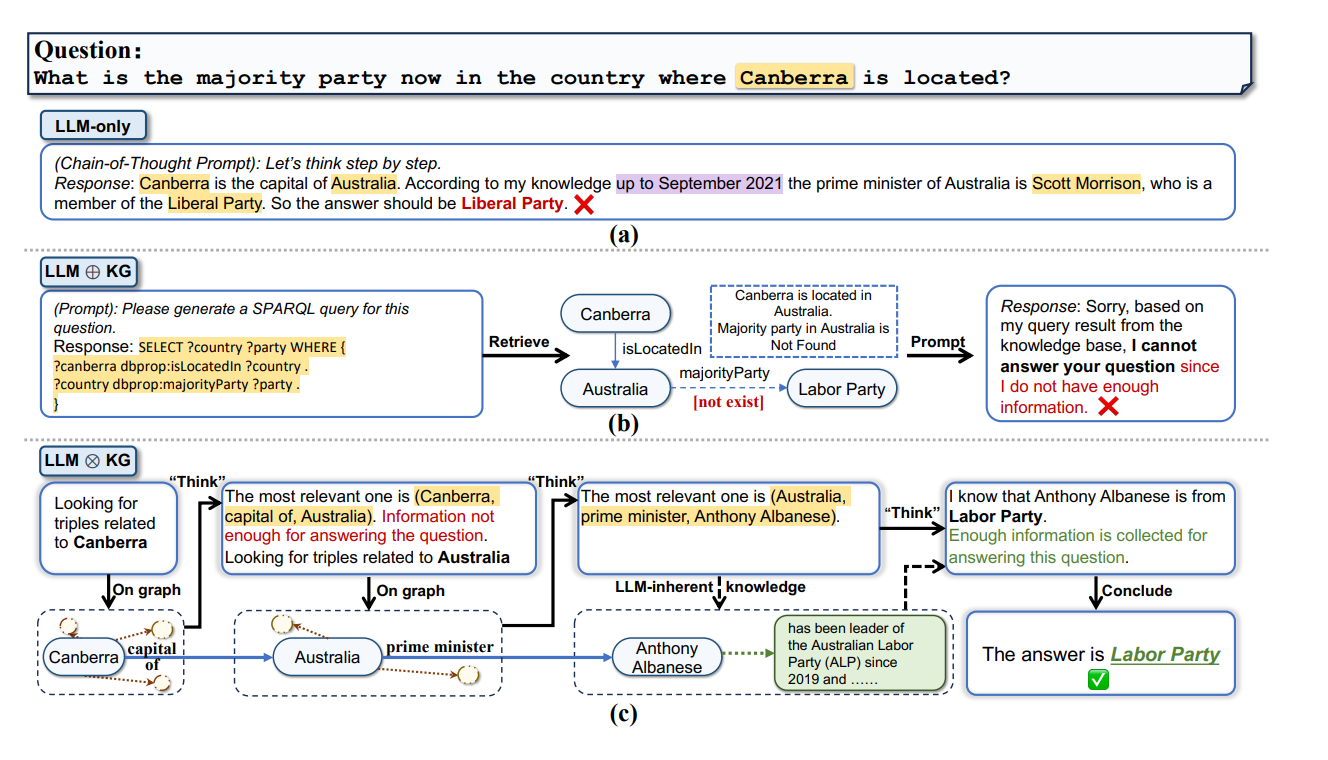
Think-on-Graph 新技术 对比 之前的技术:
(a) LLM-only(只有大模型的情况):
在这个例子中,LLM独立地尝试回答问题:“What is the majority party now in the country where Canberra is located?”。
LLM使用的是链式思考,首先确认堪培拉是澳大利亚的首都,然后基于2021年9月的信息,认为澳大利亚总理是斯科特·莫里森,属于自由党,所以答案应该是自由党。
然而,这个答案是错误的,因为LLM的知识是过时的。
(b) LLM ⊕ KG(例如,通过LLM生成的SPARQL查询):
在这种范式下,LLM首先生成一个SPARQL查询来检索知识图谱(KG)。
在这个例子中,查询是为了找到堪培拉的国家,并检索该国家的主要政党。
由于知识图谱中不存在“majority party”的相关信息,这种方法未能得出正确答案。
© LLM ⊗ KG(例如,Think-on-Graph):
这个范式展示了LLM与知识图谱紧密协作。
首先,LLM通过探索知识图谱中与堪培拉有关的三元组(triples)。
然后,通过“Think”步骤,它找到了最相关的三元组是(澳大利亚,首相,安东尼·阿尔巴尼斯)。
由于LLM知道安东尼·阿尔巴尼斯属于劳工党,并且自2019年以来一直是澳大利亚劳工党(ALP)的领导者,因此能够推断出正确答案是劳工党。
所以,Think-on-Graph 这种LLM与知识图谱的新技术,效果也是最好的。
- LLM ⊗ KG (Think-on-Graph) 方法通过结合LLM的动态推理能力和KG的丰富、结构化知识
- 显著提升了解答的准确性和可靠性
- 解决了仅使用LLM时的知识过时问题 和 LLM与KG结合时的信息缺失问题
Think-on-Graph 工作流程:

工作流程分为三个深度搜索阶段(Depth 1、Depth 2、Depth 3),逐步深化搜索,每个阶段都深入探索与前一阶段发现的实体相关的更多信息。
- 以回答问题:“堪培拉所在的国家目前的主要政党是什么?”
-
Depth 1:识别问题中的关键实体(堪培拉)和与其直接相关的属性(它是哪个国家的首都)。
- 搜索: 以堪培拉为中心,探索相关实体和关系。
- 剪枝: 对探索结果进行评估,保留重要的实体和关系,淘汰评分低的部分。在这个阶段,确定堪培拉是一个地域,是澳大利亚的首都。
-
Depth 2:以第一阶段确定的国家(澳大利亚)为中心,进一步探索与政府头目(首相)相关的信息。
- 搜索: 以澳大利亚为中心,进一步探索与政府、首相等相关的实体和关系。
- 剪枝: 继续评估和淘汰,确定了澳大利亚的首相是安东尼·阿尔巴尼斯。
-
Depth 3:最后,确定首相(安东尼·阿尔巴尼斯)的政党隶属,从而得出国家的主要政党。
- 搜索: 最后以安东尼·阿尔巴尼斯为中心,搜索与政党相关的实体和关系。
- 剪枝: 最终找到安东尼·阿尔巴尼斯与劳工党的关系。
在每个深度的搜索和剪枝过程中,发光的实体代表中心实体,粗体实体代表被选中的中心实体。
图中的边缘的黑暗度代表了由LLM给出的评分,虚线表示由于评分低而被剪枝的关系(精准回答,避免模糊宽泛)。
最终,基于这些推理路径,生成的答案是“Labor Party”(劳工党)。
本质:ToG通过逐步深入的探索和剪枝过程,结合LLM的推理能力和KG的丰富数据,动态构建推理路径以提供精准且可追溯的答案。
ToG 算法步骤:想想再查,查查再想
ToG方法的主要问题是如何利用LLM进行深度推理以回答基于知识图谱的复杂问题。
ToG是通过 beam search 在知识图谱上执行搜索,以此来解决问题。
-
子问题1:初始化图搜索。
- 子解法1:定位初始实体。
之所以使用这个解法,是因为需要在知识图谱中确定起始点,这是构建推理路径的基础。
- 子解法1:定位初始实体。
-
子问题2:探索。
- 子解法2.1:关系探索。
用于从当前已知实体探索可能的关系,因为这有助于确定接下来可能的推理方向。 - 子解法2.2:实体探索。
接着用于从已知关系探索相关实体,因为这可以进一步扩展推理路径。
- 子解法2.1:关系探索。
-
子问题3:推理。
- 子解法3:评估推理路径。
之所以使用此解法,是因为需要评估当前推理路径是否足够回答问题,如果足够则生成答案,否则继续探索和推理过程。
- 子解法3:评估推理路径。
还有 ToG-R(基于关系的Think-on-Graph 变种):
-
子问题1:减少LLM调用次数。
- 子解法1:随机剪枝。
之所以使用这个解法,是因为它减少了使用LLM进行实体剪枝的需要,这样可以降低总体成本和推理时间。
- 子解法1:随机剪枝。
-
子问题2:强调关系文字信息。
- 子解法2:关系链探索。
选择这种解法是因为它强调了关系的文字信息,当中间实体的文字信息缺失或LLM不熟悉时,可以减少误导推理的风险。
- 子解法2:关系链探索。
ToG 方法的本质在于,通过LLM执行的知识图谱上的beam search,分阶段探索和评估推理路径,以便深度推理出复杂问题的精确答案,而 ToG-R 进一步减少了LLM调用,强调文字信息,提高了效率和鲁棒性。
- 初始化图搜索的问题,通过定位初始实体的子解法来解决。
- 探索问题,通过关系探索和实体探索两个子解法来解决。
- 推理问题,通过评估推理路径的子解法来解决。
- ToG-R 特有的问题,通过随机剪枝和关系链探索两个子解法来解决。

假设我们要回答的问题是:“谁是最近一次举办奥运会的国家的现任总统?”
-
初始化图搜索:
- 我们首先利用LLM确定问题中的关键实体“最近一次举办奥运会的国家”,并将其作为搜索的起始点。
-
探索:
- 关系探索:
在知识图谱中搜索与“奥运会举办国”相关的实体关系,比如“举办年份”和“国家”。 - 实体探索:
接下来,我们基于“举办年份”这一关系,探索出最近一次举办奥运会的具体国家,例如“日本”。
- 关系探索:
-
推理:
- 根据已经探索到的信息,评估是否有足够的数据来回答原问题。
- 如果已知的国家“日本”和关系“现任总统”足够回答问题,我们就进行下一步;
- 如果不足够,就需要进一步的探索和推理。
在ToG-R中,如果在实体探索阶段关系信息不够充分,我们可能会采用随机剪枝策略,选择一个可能的实体,例如随机选择一位政治人物,然后继续下一轮探索。
实验结果
ToG这个算法通过在各种不同的数据集上的测试显示出它很擅长处理需要多步逻辑推理的复杂问题,这得益于它能够在多个层面上全面理解和应用知识图谱中的信息。
- 在和其他方法的比较中,ToG特别展现了它的泛化能力,即使在没有针对特定问题集进行训练的情况下,它也能提供准确的答案。
实验中还特别考察了不同大小的语言模型对ToG的影响。
- 结果表明,更大的模型能够更好地发挥知识图谱的潜力,但即便是较小的模型,ToG也能超越只用最大模型的传统方法。
- 这意味着使用ToG,我们可以用更经济的小模型来代替昂贵的大模型,特别是在那些外部知识图谱能提供帮助的特定场景中。
此外,ToG的性能也受到搜索深度和宽度的影响,通过调整这两个参数,ToG的表现有所提升,尽管提升的幅度在深度超过一定阈值后会减弱。
- 在提高性能的同时也要考虑到计算成本。
不同知识图谱的选择也对ToG的表现有显著影响。
-
例如,在构建于Freebase上的数据集中,ToG的表现更好,这显示了匹配度高的知识图谱对提升性能至关重要。
-
而且,不同的提示设计,如三元组格式相比自然语言句子,对于ToG来说也有更好的效果。
在探索过程中使用不同的剪枝工具也会影响ToG的表现。
- 实验表明,与BM25或SentenceBERT相比,使用LLM作为剪枝工具可以获得更好的结果,尽管后者在效率上有优势。
最后,ToG的一个独特之处在于它提供了知识的追溯性和可校正性。
- 如果用户发现了推理过程中的错误,他们可以通过ToG回溯并纠正知识图谱中的错误信息。
- 不仅增强了LLM使用知识图谱的能力,还提升了知识图谱本身的质量。

)

——编码信道数学模型)



缓存双写一致性策略)

)

)
)



|Day39(动态规划))


