回归 VS 分类

• 回归估计一个连续值
• 分类预测一个离散类别

---

从回归到多类分类

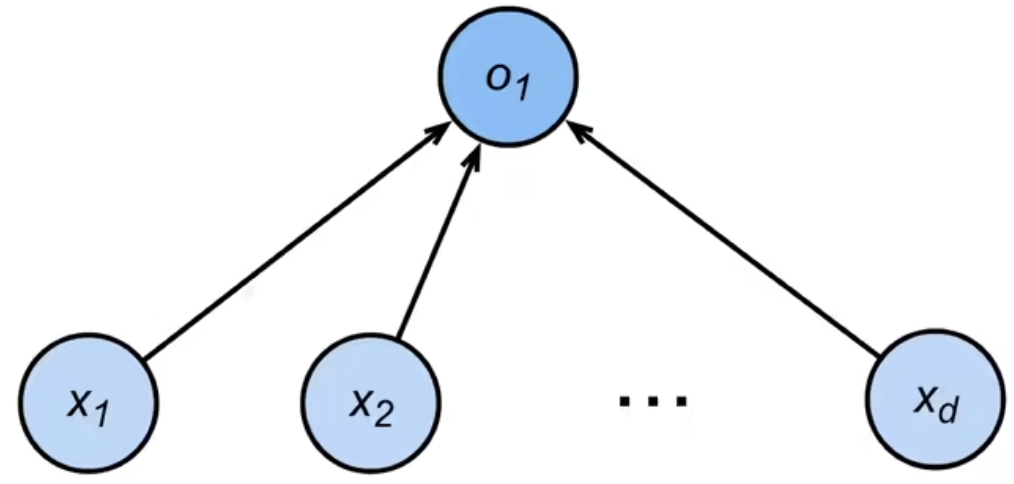
回归

• 单连续数值输出
• 输出的区间：自然区间 $\mathbb{R}$
• 损失：跟真实值的区别
  

分类

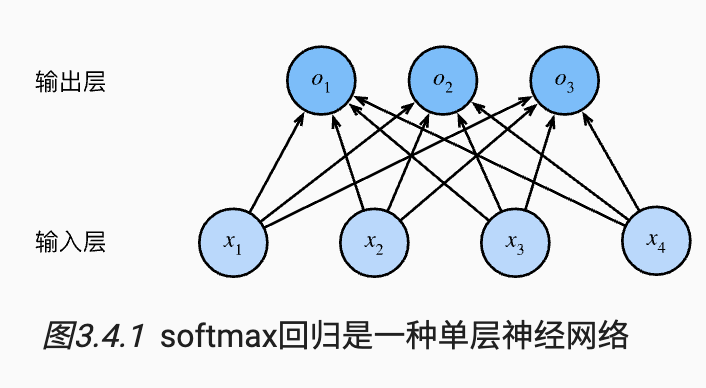
• 通常多个输出（这个输出的个数是等于类别的个数）
• 输出的第$i$个元素是用来预测第$i$类的置信度
  

---

从回归到多类分类——均方损失

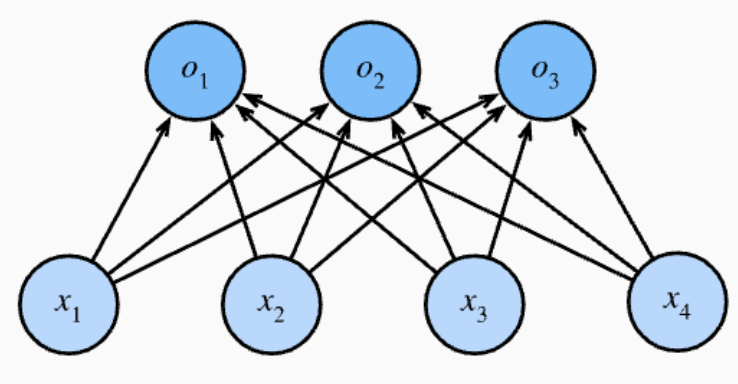
• 对类别进行一位有效编码（因为类别不是一个数，可能是一个字符串等等）
  假设我们有$n$个类别，我们可以用最简单的一位有效编码来进行编码。假设我们有$n$个类别，那么我们的标号就是一个长为$n$的向量，从$y_1$到$y_n$，其中，假设我的真实的类别是第$i$个，那么$y_i$等于$1$，其他的元素全部等于$0$。意思就是这个向量中，我们恰好有一个位置为$1$，这个位置的下标表示第$i$个元素，其他的元素全部为$0$。
  $$y=[y_1,y_2,...,y_n{]}^T$$
  $$y_i=\{\begin{array}{l}1ifi=y\\ 0otherwise\end{array}$$
• 使用均方损失训练(当我们有了编码以后，我们可以用最简单的回归问题的均方损失来训练，我们可以在不改动的情况下)
• 最大值最为预测（假设我们有我们训练出来的一个模型，我们做预测的时候，那么就是我们选取$i$时的最大化$o_i$即置信度的值，作为我的预测，$i$是我们预测的一个标号）
  $$\hat{y}=\underset{i}{\mathrm{argmax}}{o}_i$$

---

从回归到多类分类——无校验比例

对于分类来讲，我们其实不关心，它们之间的实际的值，我们关心的是说，我是不是能够对正确类别的置信度特别大。

我们可以将我们的目标函数改为，我们需要使得我们对正确类$y$的置信度，就是$o_y$，要远远大于其他非正确类的$o_i$，要大于某一个阈值，$\Delta$。
这样子能保证我的模型真正地能够将我的真正的类和不一样的类拉开距离。

虽然我们这里没有说你具体$o_i$要什么样的值，大一点小一点都没关系，我们关心的是一个相对值，但是我们如果把值放在一个合适的区间，也会让我们后面的变得更加简单。

• 对类别进行一位有效编码

• 最大值最为预测$$\hat{y}=\underset{i}{\mathrm{argmax}}{o}_i$$

• 需要更置信的识别正确类（大余量）
  $$o_y-o_i\ge \Delta (y,i)$$

从回归到多类分类——校验比例

我们希望使得我们的输出能够是一个概率，现在我们的输出是$o_1$一直到$o_n$，就是一个$o$的一个向量。那么我们怎么做这个事情呢？
我们可以引入一个新的操作子，叫做$softmax$，我们将$softmax$作用在$o$上面，得到一个$\hat{y}$,它是一个长为$n$的向量，但是它有我们要的属性，即它的每个元素都非负，而且它的和为1。

• 输出匹配概率（非负，和为$1$）
  $$\hat{y}=softmax(o)$$$${\hat{y}}_i=\frac{exp(o_i)}{{\sum }_{k}exp(o_k)}$$具体我们的操作是说，$\hat{y}$里面的第$i$个元素，它是等于$o$里面的第$i$个元素，作指数，指数的好处是说我不管它里面的值是多少，我都能够把它变成非负；再除以所有的$o_k$作指数的和，这样我们能够保证$\hat{y}$所有的元素加起来的和为$1$。这样的好处就是说，我们的$\hat{y}$它其实就是一个概率啦。

回忆一下，我们对真实标号的$y$，也是作成一个概率，因为他刚好只有一个元素为$1$，剩下的全部为$0$，任何满足所有元素非负，且和为$1$的，都可以当作一个概率。
那么我们就得到两个概率，一个是真实的$y$的概率，一个是预测的$\hat{y}$的概率。

• 概率$y$和$\hat{y}$的区别作为损失

---

Softmax和交叉熵损失

我们假设有两个离散概率$p$和$q$，都有$n$个元素

• 交叉熵常用来衡量两个概率的区别$H(p,q)=\sum _i-p_{i}log(q_i)$
• 将它作为损失
  $$l(y,\hat{y})=-\sum _i{y}_{i}log{\hat{y}}_i=-log{\hat{y}}_y$$我们知道，真实值里面只有$1$个为$1$，其余都为$0$，因而公式可以简写为，负的$log$对真实类别$y$它的预测的$\hat{y}$，就是对真实类别我的预测值求$log$然后求负数。
  可以看到，对分类问题来讲，我们不关心对非正确类的预测值，我们只关心对正确类的预测值它要执行度要多大。
• 其梯度是真实概率和预测概率的区别
  $${\partial }_{o_i}l(y,\hat{y})=softmax(o{)}_i-y_i$$
  
  
  

---

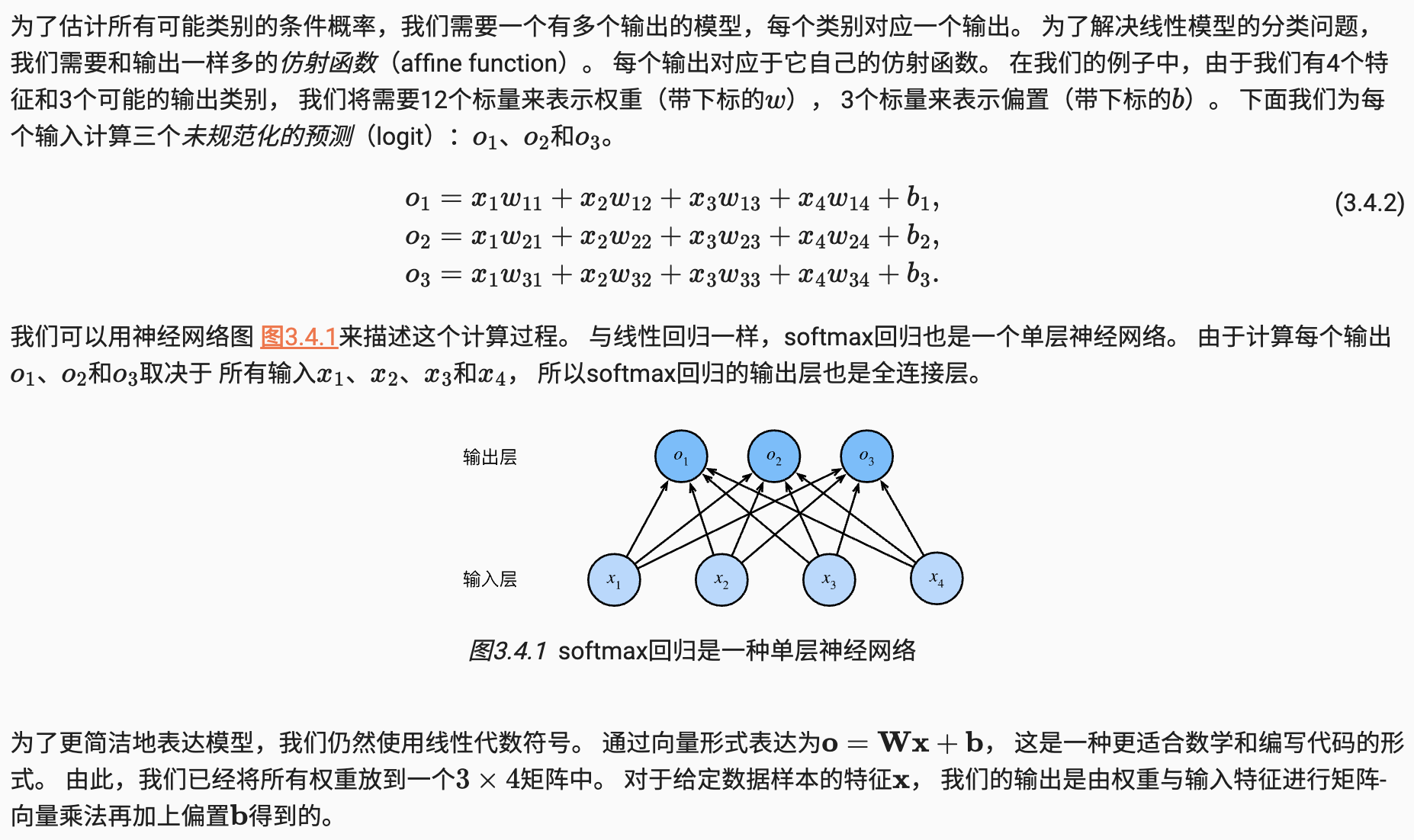
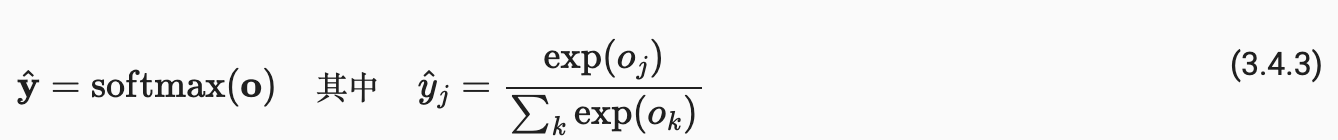
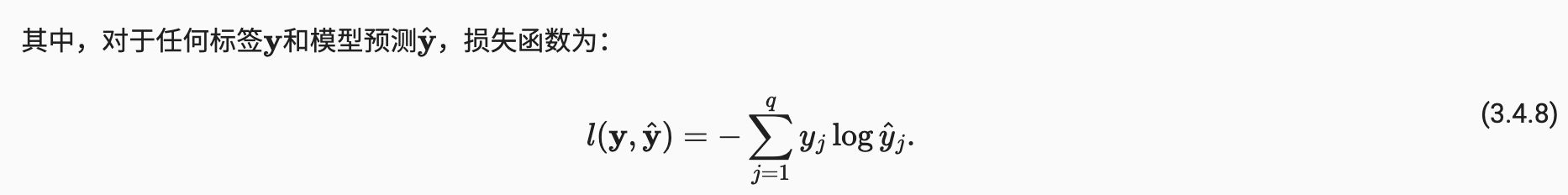
总结

• Softmax回归是一个多类分类模型
• 使用Softmax操作子得到每个类的预测置信度
• 使用交叉熵来衡量预测和标号的区别