Tensor中统计学相关的函数
torch.mean() #返回平均值
torch.sum() #返回总和
torch.prod() #计算所有元素的积
torch.max() # 返回最大值
torch.min() # 返回最小值
torch.argmax() #返回最大值排序的索引值
torch.argmin() #返回最小值排序的索引值
torch.std() #返回标准差
torch.var() #返回方差
torch.median() #返回中间值
torch.mode() #返回众数值
torch.histc() #计算input的直方图
torch.bincount() #返回每个值得频数
分布函数
Tensor的torch.distributions
distributions 包含可参数化的概率分布和采样函数
- 得分函数
- 强化学习中策略梯度方法的基础
- pathwise derivative估计器
- 变分自动编码器中的重新参数化技巧
- ExponentialFamily、Bernoulli、Categorical、 Beta、 Binomial.Cauchy、Chi2、Dirichlet、Exponential、 FisherSnedecor.Gamma、Geometric、Gumbel、HalfCauchy、HalfNormal.Independent、 Laplace、 LogNormal、LowRankMultivariateNormal、Multinomial、 MultivariateNormalNegativeBinomial、Normal、OneHotCategorical、 Pareto、Poisson、RelaxedBernoulli、RelaxedOneHotCategorical.StudentT、TransformedDistribution、Uniform、 Weibul
Tensor中的随机抽样
- 定义随机种子
- torch.manual_seed(seed)
- 定义随机数满足的分布
- torch.normal()
Pytorch与线性代数运算
Tensor中的范数运算
范数
- 在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即 非负性、齐次性、三角不等式
- 常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小
0范数/1范数/2范数/p范数/核范数
- torch.dist(input, other p=2)计算p范数
- torch.norm()计算2范数
Tensor中的矩阵分解
常见的矩阵分解
- LU分解:将矩阵A分解成L(下三角)矩阵和U(上三角)矩阵的乘积
- QR分解:将原矩阵分解成一个正交矩阵Q和一个上三角矩阵R的乘积
- EVD分解:特征值分解
- SVD分解:奇异值分解
特征值分解
- 将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法
- 特征值 VS 特征向量
PCA与特征值分解
- PCA:将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征
- PCA算法的优化目标就是
- 降维后同一纬度的方差最大
- 不同维度之间的相关性为0
- 协方差矩阵
奇异值分解
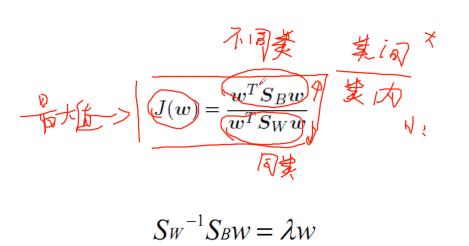
LDA与奇异值分解
EVD分解 VS SVD分解
- 矩阵方阵且满秩(可对角化)
- 矩阵分解不等于特征降维度
- 协方差矩阵描述方差和相关性
Pytorch中的奇异值分解
- torch.svd()
