目录

题目地址：

题目：

我们直接看题解吧：

解题分析：

解题思路：

代码实现：

代码补充说明：

代码实现(中序遍历)：

---

题目地址：

98. 验证二叉搜索树 - 力扣（LeetCode）

难度：中等

今天刷验证二叉搜索树，大家有兴趣可以点上面链接，看看题目要求，试着做一下。

题目：

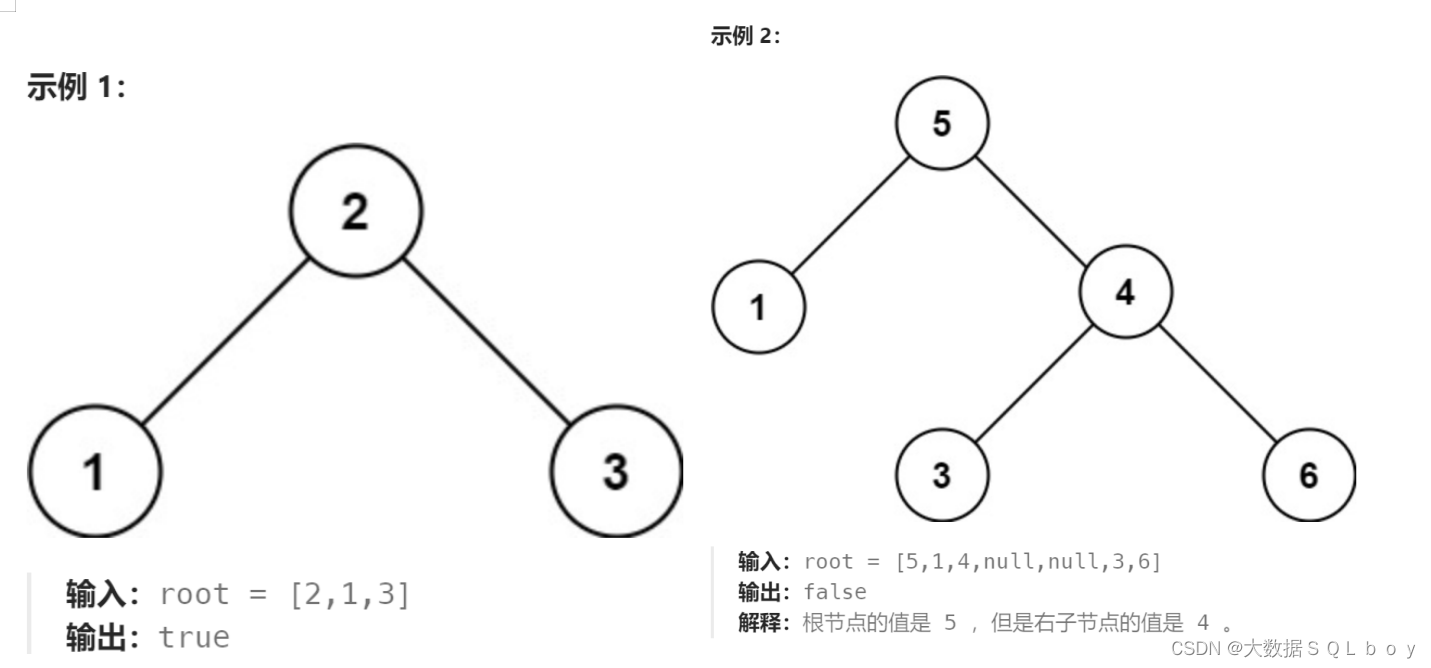
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

 

我们直接看题解吧：

快速理解解题思路小建议：

可以先简单看一下解题思路，然后照着代码看思路，会更容易理解一些。

解题方法：

方法1，递归

方法2，中序遍历

中序遍历相关题目及解题：

二叉树的中序遍历，力扣-CSDN博客

解题分析：

由题意可知二叉搜索树的定义：

  · 如果该二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；

   · 若该二叉树的右子树不空，则右子树上所有节点的值均大于它的根节点的值；

  ·它的左右子树也为二叉搜索树。

解题思路：

      1、核心思路：

设计递归函数以root为根的子树，判断子树中所有的节点的值是否在(l,r)区间范围内(开区间)

   若满足范围要求则继续调用它的左右子树是否满足(若都满足则为二叉树)，

   若不满足则直接返回false

    2、具体递归调用：

递归调用左子树，需将上界upper改为root.val，即左子树的所有节点的值均小于它的根节点的值；

 递归递归调用右子树，则需要将下界lower改为root.val，即右子树的所有节点的值均大于它的根节点的值；

可结合力扣解题思路-->98. 验证二叉搜索树 - 力扣（LeetCode） 

代码实现：

class Solution {public boolean isValidBST(TreeNode root) {return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);//函数递归入口}public boolean isValidBST(TreeNode node, long lower, long upper) {if (node == null) {  //判断节点是否null，即是否为叶子节点return true;}if (node.val <= lower || node.val >= upper) {return false;//判断范围，若不在区间范围内则返回false结束递归}return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);//若在区间范围内，则递归调用该节点的左右子树}
}

代码补充说明：

1、函数递归调用的入口为helper（root,-inf,+inf）,-inf表示long类型的最小值，+inf反之 

      注意第一次调用时上下界是不可用的，需调用其左右子树，

                -inf,+inf作用是确保不出现数据范围越界

2、为防止出现数据边界越界的问题，由于整个树的数据类型都是Int，用Int的话值会被覆盖掉，而long类型覆盖了整个Int类型的范围，因此将数据类型设置为long

 

代码实现(中序遍历)：

由中序遍历的访问特点“左节点 -> 根节点 -> 右节点”，

          再根据二叉搜索树的特点“左节点的值 < 当前结点的值 < 右节点的值”，

我们可以利用这两个特性得出：

我们在中序遍历的时候实时检查当前结点的值是否大于前一个中序遍历到的结点的值即可。

因为按照“左 -> 根 -> 右”的顺序遍历，刚好结点间的值是从小到大排序的。

所以，如果均大于则说明这个序列是升序的，整棵树是二叉搜索树，否则不是。

class Solution {long pre = Long.MIN_VALUE;//创建临时变量，存储前一节点的值，初始为long的最小值public boolean isValidBST(TreeNode root) {if (root == null) {return true;}// 访问左子树，如果左子树中任意一个节点出错就可以直接返回false，不用后续再遍历了if (!isValidBST(root.left)) {return false;}// 访问当前节点：若当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；if (root.val <= pre) {return false;}// 若当前节点大于中序遍历的前一个节点，则更新变量pre的值；pre = root.val;// 接着访问右子树return isValidBST(root.right);}
}