---

0. 引言

前情提要：
《NLP深入学习（一）：jieba 工具包介绍》
《NLP深入学习（二）：nltk 工具包介绍》
《NLP深入学习（三）：TF-IDF 详解以及文本分类/聚类用法》
《NLP深入学习（四）：贝叶斯算法详解及分类/拼写检查用法》
《NLP深入学习（五）：HMM 详解及字母识别/天气预测用法》
《NLP深入学习（六）：n-gram 语言模型》
《NLP深入学习（七）：词向量》
《NLP深入学习（八）：感知机学习》
《NLP深入学习（九）：KNN 算法及分类用法》
《NLP深入学习（十）：决策树（ID3、C4.5以及CART）》
《NLP深入学习（十一）：逻辑回归（logistic regression）》

1. 什么是支持向量机

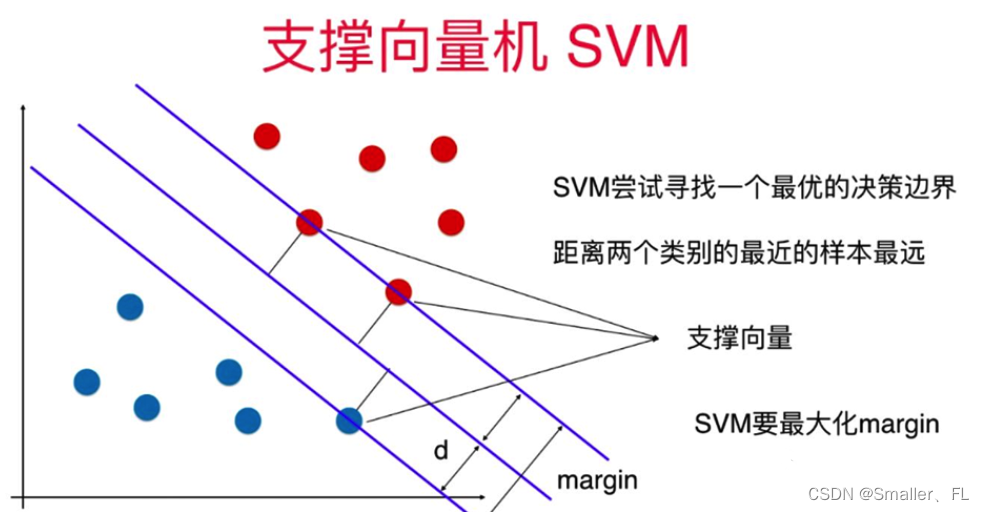
支持向量机（Support Vector Machine, SVM）是一种监督学习模型，主要用于分类和回归分析任务，但最常用于二分类问题。其核心思想是通过构建一个能够最大化类别间隔（margin）的超平面来划分不同类别的数据点。

在二维或三维空间中，超平面是一个线性决策边界，而在高维特征空间中，则是一个多维的分割面。SVM的目标是最小化误分类点到这个超平面的距离（即找到最大间隔超平面），这样不仅可以使得模型具有很好的泛化能力，而且对未知样本的预测更加稳定。

对于非线性可分的数据集，SVM使用核函数（Kernel Trick）将原始输入数据映射到高维特征空间，在这个新的空间中寻找最优的超平面。常用的核函数包括线性核、多项式核、高斯核（径向基函数，RBF）等。

2. 线性 SVM

线性可分支持向量机（Linearly Separable Support Vector Machine）是 SVM 的一个特例，它假设训练数据是线性可分的，即存在一个超平面能够将正类别和负类别的样本完全分开。

以下是线性可分支持向量机的推导过程：

1. 假设我们有训练数据集：$\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$，其中 $x_i$ 是输入样本， $y_i$ 是对应的类别标签（+1 或 -1）。

2. 我们的目标是找到一个超平面，表示为 $w\cdot x+b=0$，其中 $w$ 是法向量（weights）， $b$ 是偏置（bias）。

3. 超平面将空间分成两个区域：正类别和负类别。我们希望对于所有的 $i$，如果 $y_i=1$，则 $w\cdot x_i+b>0$，如果 $y_i=-1$，则 $w\cdot x_i+b<0$。

4. SVM 的优化目标是最大化超平面到最近的正类别和负类别样本之间的间隔。这个间隔由超平面到最近的支持向量（支持向量是离超平面最近的训练样本）的距离决定。

5. 支持向量到超平面的距离公式是：$\text{distance}=\frac{|w\cdot x+b|}{\Vert w\Vert }$。

6. 为了最大化间隔，我们需要最小化 $\Vert w\Vert$，即最小化 $\frac{1}{2}\Vert w{\Vert }^2$（这个因子出现是为了方便后续求导）。

7. SVM 的目标函数为：
   $$\text{min}\frac{1}{2}\Vert w{\Vert }^2$$
   约束条件为：
   $$y_i(w\cdot x_i+b)\ge 1,\text{for all}i=1,2,...,n$$

8. 利用拉格朗日乘子法，我们将目标函数和约束条件转化为拉格朗日函数：
   $$\mathcal{L}(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^n{\alpha }_i\left[y_i(w\cdot x_i+b)-1\right]$$
   其中，${\alpha }_i$ 是拉格朗日乘子。

9. 对 $\mathcal{L}$ 分别对 $w$ 和 $b$ 求偏导数并令其等于零，得到：
   $$w=\sum _{i=1}^n{\alpha }_i{y}_i{x}_i$$
   $$\sum _{i=1}^n{\alpha }_i{y}_i=0$$

10. 将以上结果代入拉格朗日函数，得到拉格朗日对偶问题：
    $$\text{max}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)$$
    约束条件为：
    $${\alpha }_i\ge 0,\sum _{i=1}^n{\alpha }_i{y}_i=0$$

11. 最优解 ${\alpha }^{\ast }$ 被找到后，可以通过 $w^{\ast }={\sum }_{i=1}^n{\alpha }_i^{\ast }{y}_i{x}_i$ 计算得到超平面的法向量， $b^{\ast }$ 由支持向量计算得到。

3. 非线性 SVM

3.1 推导过程

非线性支持向量机（Nonlinear Support Vector Machine）通过引入核函数来处理非线性可分的情况。核函数允许我们将数据映射到高维空间，使得在高维空间中数据变得线性可分。以下是非线性支持向量机的推导过程：

假设我们有训练数据集：$\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$，其中 $x_i$ 是输入样本， $y_i$ 是对应的类别标签（+1 或 -1）。

1. 我们引入一个映射函数 $\varphi :{\mathbb{R}}^d\to {\mathbb{R}}^D$，将原始输入空间映射到更高维的特征空间，其中 $D$ 是高维空间的维数。

2. 我们的目标是在特征空间中找到一个线性可分的超平面。超平面表示为 $w\cdot \varphi (x)+b=0$，其中 $w$ 是法向量（weights）， $b$ 是偏置（bias）。

3. SVM 的优化目标是最大化间隔，即最小化 $\Vert w\Vert$。目标函数为：
   $$\text{min}\frac{1}{2}\Vert w{\Vert }^2$$
   约束条件为：
   $$y_i(w\cdot \varphi (x_i)+b)\ge 1,\text{for all}i=1,2,...,n$$

4. 利用拉格朗日乘子法，我们将目标函数和约束条件转化为拉格朗日函数：
   $$\mathcal{L}(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^n{\alpha }_i\left[y_i(w\cdot \varphi (x_i)+b)-1\right]$$
   其中，${\alpha }_i$ 是拉格朗日乘子。

5. 对 $\mathcal{L}$ 分别对 $w$ 和 $b$ 求偏导数并令其等于零，得到：
   $$w=\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x_i)$$
   $$\sum _{i=1}^n{\alpha }_i{y}_i=0$$

6. 将以上结果代入拉格朗日函数，得到拉格朗日对偶问题：
   $$\text{max}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)$$
   约束条件为：
   $${\alpha }_i\ge 0,\sum _{i=1}^n{\alpha }_i{y}_i=0$$

   这里，$K(x_i,x_j)$ 是核函数，它表示在特征空间中点 $x_i$ 和 $x_j$ 的内积。

7. 选择适当的核函数，如线性核、多项式核、高斯核等，根据问题的性质来进行非线性映射。

8. 最优解 ${\alpha }^{\ast }$ 被找到后，可以通过 $w^{\ast }={\sum }_{i=1}^n{\alpha }_i^{\ast }{y}_i\varphi (x_i)$ 计算得到超平面的法向量， $b^{\ast }$ 由支持向量计算得到。

这样，通过引入核函数，我们可以处理非线性可分的情况，将数据映射到高维空间中，然后在高维空间中寻找线性可分的超平面。

3.2 常用核函数

核函数在非线性支持向量机中扮演着关键的角色，它用于将输入数据映射到高维空间，从而使得在高维空间中的数据更容易被线性分割。以下是一些常用的核函数：

1. 线性核函数（Linear Kernel）：
   $$K(x_i,x_j)=x_i\cdot x_j$$
   简单的内积操作，适用于线性可分的情况。

2. 多项式核函数（Polynomial Kernel）：
   $$K(x_i,x_j)=(x_i\cdot x_j+c{)}^d$$
   其中，$c$ 是常数，$d$ 是多项式的次数。通过调整 $c$ 和 $d$ 可以实现不同程度的非线性映射。

3. 高斯径向基核函数（Gaussian Radial Basis Function, RBF）：
   $$K(x_i,x_j)=\exp \left(-\frac{\Vert x_i-x_j{\Vert }^2}{2{\sigma }^2}\right)$$
   其中，$\sigma$ 是控制函数宽度的参数。常用于处理复杂的非线性关系，对于很多问题表现良好。

4. Sigmoid核函数：
   $$K(x_i,x_j)=\tanh (\alpha x_i\cdot x_j+c)$$
   其中，$\alpha$ 和 $c$ 是调节参数。它类似于神经网络中的激活函数。

5. 拉普拉斯核函数（Laplacian Kernel）：
   $$K(x_i,x_j)=\exp \left(-\frac{\Vert x_i-x_j\Vert }{\sigma }\right)$$
   类似于高斯核函数，但它对离中心点较远的数据点的惩罚更加明显。

6. 多项式Spline核函数：
   $$K(x_i,x_j)={\left(1+x_i\cdot x_j+\frac{(x_i\cdot x_j{)}^2}{2}\right)}^d$$
   这是一种非线性的核函数，可以通过调整参数 $d$ 来实现不同程度的非线性映射。

4. 参考

《NLP深入学习（一）：jieba 工具包介绍》
《NLP深入学习（二）：nltk 工具包介绍》
《NLP深入学习（三）：TF-IDF 详解以及文本分类/聚类用法》
《NLP深入学习（四）：贝叶斯算法详解及分类/拼写检查用法》
《NLP深入学习（五）：HMM 详解及字母识别/天气预测用法》
《NLP深入学习（六）：n-gram 语言模型》
《NLP深入学习（七）：词向量》
《NLP深入学习（八）：感知机学习》
《NLP深入学习（九）：KNN 算法及分类用法》
《NLP深入学习（十）：决策树（ID3、C4.5以及CART）》
《NLP深入学习（十一）：逻辑回归（logistic regression）》

欢迎关注本人，我是喜欢搞事的程序猿； 一起进步，一起学习；

也欢迎关注我的wx公众号：一个比特定乾坤