文章目录
- 零、前言
- 一、二分图匹配转化为网络流模型
- 1.1建模步骤
- 1.2整数值最大流和二分图匹配的关系
- 1.3代码实现
- 二、OJ练习
- P2756 飞行员配对方案问题
- P3254 圆桌问题
零、前言
阅读本文前,需具备以下知识:
二分图及染色法判定-CSDN博客
二分图最大匹配——匈牙利算法详解-CSDN博客
最大流—EK算法,流网络,残留网络,定理证明,详细代码-CSDN博客
最大流-Dinic算法,原理详解,四大优化,详细代码-CSDN博客
一、二分图匹配转化为网络流模型
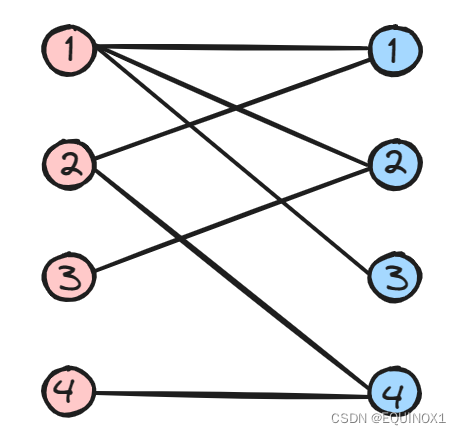
1.1建模步骤
- 二分图G中创建虚拟源点s,虚拟汇点t,s和左部点边,t和右部点连边
- 得到新图G‘,新图G’中所有边容量设为1
- 在G‘中寻找整数值最大流f,原二分图G中所有有流量的边即为最大匹配
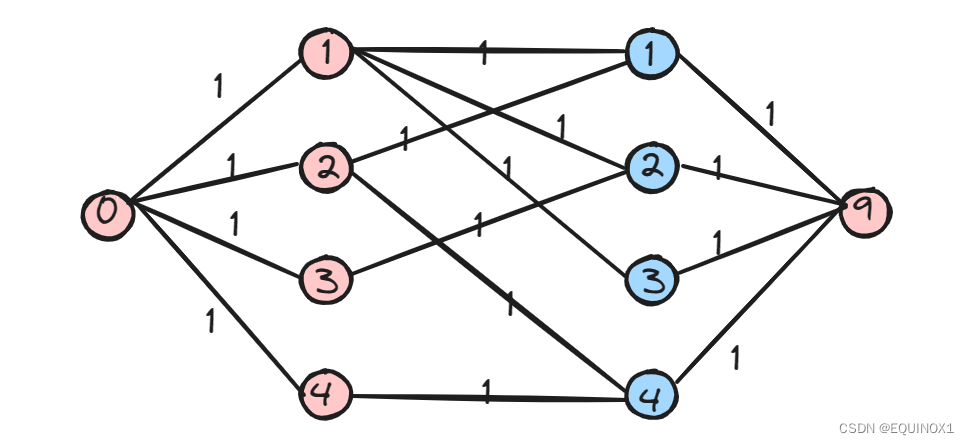
1.2整数值最大流和二分图匹配的关系
对于流网络中的最大流,不一定为整数,也可以是浮点数,所以我们有两个问题:
整数值可行流是否是二分图中一个匹配,二分图中的一个匹配是否对应一个整数值可行流?
对于可行流而言,由于所有边的容量上限都为1,所以每个左部点最多流经1点流量,也最多将这1点流量流向一个右部点,即每个左部点最多和一个右部点建立流量,换句话说,任取两条有流量的边,必然没有公共点,所以可行流是一个匹配。
那么对于一个匹配而言,我们匹配边赋予1点流量,再建立虚拟源点和虚拟汇点,我们发现新图除源汇点外满足容量守恒,斜对称和容量限制,所以是一个可行流。
于是建立了整数可行流和二分图最大匹配之间的双射关系。
为什么一定能找到一个整数值最大流?
由于建立的流网络中只用到了整数值,我们求解最大流的算法也都只用到了整数值,所以最大流一定是整数流
1.3代码实现
以P3386 【模板】二分图最大匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)为模板
时间复杂度:(On m^0.5)
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int N = 1010, M = (50000 + N) << 1, inf = 1e9;
struct edge
{int v, c, nxt;
} edges[M];
int n, m, e, s, t, head[N], d[N], cur[N], idx = 0;
inline void addedge(int u, int v, int c)
{edges[idx] = {v, c, head[u]}, head[u] = idx++;
}
inline void add(int u, int v, int c)
{addedge(u, v, c), addedge(v, u, 0);
}
int dfs(int u, int limit)
{if (u == t)return limit;int res = 0;for (int i = cur[u]; ~i && limit; i = edges[i].nxt){cur[u] = i;int v = edges[i].v;if (d[v] == d[u] + 1 && edges[i].c){int incf = dfs(v, min(limit, edges[i].c));if (!incf)d[v] = 0;limit -= incf, res += incf, edges[i].c -= incf, edges[i ^ 1].c += incf;}}return res;
}
bool bfs()
{memset(d, 0, sizeof(d));queue<int> q;q.emplace(s), d[s] = 1;while (q.size()){int u = q.front();q.pop();for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (!d[v] && edges[i].c){d[v] = d[u] + 1, q.emplace(v);if (v == t)return true;}}}return false;
}
int dinic()
{int res = 0;while (bfs())memcpy(cur, head, sizeof(head)), res += dfs(s, inf);return res;
}
int main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0), memset(head, -1, sizeof(head));// freopen("in.txt", "r", stdin);int a, b, c;cin >> n >> m >> e, s = 0, t = n + m + 1;for (int i = 0; i < e; i++)cin >> a >> b, add(a, b + n, 1);for (int i = 1; i <= n; i++)add(s, i, 1);for (int i = 1; i <= m; i++)add(i + n, t, 1);cout << dinic();return 0;
}
二、OJ练习
P2756 飞行员配对方案问题
P2756 飞行员配对方案问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
很显然是一个二分图最大匹配问题,建图跑板子即可,然后题目还要求我们输出匹配边的两个节点,我们遍历匹配边,反向边和正向边的邻接点即为两个匹配点
F1 Dinic
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <queue>
#include <unordered_set>
#include <map>
#include <bitset>
using namespace std;
#define sc scanf
#define int long long
#define N 105
#define M 10010
const int MOD = 10000007;
const int inf = 0x3f3f3f3f3f3f3f3f;int n, m, s, t, idx = 0;
int d[N], cur[N], head[N]; // 深度,当前边,前向星头
struct edge
{int v, c, nxt;
} edges[M];inline void addedge(int u, int v, int c)
{edges[idx] = {v, c, head[u]};head[u] = idx++;
}bool bfs() // 多路增广
{memset(d, 0, sizeof(d));queue<int> q;q.emplace(s), d[s] = 1;while (q.size()){int u = q.front();q.pop();for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (!d[v] && edges[i].c){d[v] = d[u] + 1;q.emplace(v);if (v == t)return true;}}}return false;
}int dfs(int u, int limit)
{if (u == t)return limit;int ret = 0;for (int i = cur[u]; ~i && limit > 0; i = edges[i].nxt){cur[u] = i;int v = edges[i].v;if (d[v] == d[u] + 1 && edges[i].c){int incf = dfs(v, min(limit, edges[i].c));if (!incf)d[v] = 0;edges[i].c -= incf, edges[i ^ 1].c += incf, ret += incf, limit -= incf;}}return ret;
}int dinic()
{int ret = 0;while (bfs())memcpy(cur, head, sizeof(head)), ret += dfs(s, inf);return ret;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// freopen("in.txt", "r", stdin);memset(head, -1, sizeof(head));cin >> m >> n;int a, b;s = 0, t = n + 1;memset(head, -1, sizeof(head));for (int i = 1; i <= m; i++)addedge(s, i, 1), addedge(i, s, 0);for (int i = m + 1; i <= n; i++)addedge(i, t, 1), addedge(t, i, 0);while (1){cin >> a >> b;if (a == -1 && b == -1)break;addedge(a, b, 1), addedge(b, a, 0);}cout << dinic() << '\n';for (int i = 0; i < idx; i += 2)if (edges[i].v > m && edges[i].v <= n && !edges[i].c)cout << edges[i ^ 1].v << " " << edges[i].v << '\n';
}F2 匈牙利求最大匹配
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <queue>
#include <unordered_set>
#include <map>
#include <bitset>
using namespace std;
#define sc scanf
#define int long long
#define N 105
#define M 10010
const int MOD = 10000007;
const int inf = 0x3f3f3f3f3f3f3f3f;int n, m, idx, ans = 0;
int match[N]{0}, head[N];
bool vis[N];
struct edge
{int v, nxt;
} edges[M << 1];inline void addedge(int u, int v)
{edges[idx] = {v, head[u]};head[u] = idx++;
}bool dfs(int u)
{for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (vis[v])continue;vis[v] = 1;if (!match[v] || dfs(match[v])){match[v] = u;return true;}}return false;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// freopen("in.txt", "r", stdin);memset(head, -1, sizeof(head));cin >> m >> n;int a, b;memset(head, -1, sizeof(head));while (1){cin >> a >> b;if (a == -1 && b == -1)break;addedge(a, b);}for (int i = 1; i <= m; i++)memset(vis, 0, sizeof(vis)), ans += dfs(i);cout << ans << '\n';for (int i = m + 1; i <= n; i++)if (match[i])cout << match[i] << " " << i << '\n';
}
P3254 圆桌问题
P3254 圆桌问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
仍然是二分图最大匹配,不过这里是多重匹配,处理多重匹配我们的策略是拆点,当然可以用匈牙利来做,这里我们直接用Dinic,体会一下如何将问题抽象为网络流问题。
这里建图相较于匈牙利解法就很爽了,每个左部点右部点最大连边数就是它们跟源点汇点边的容量,然后左右部点之间互相连容量为1的边,然后跑板子即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;const int N = 430, M = (150 * 270 + N) * 2;
const int inf = 1e9;
int n, m, s, t, idx = 0, cur[N], head[N], d[N];
struct edge
{int v, c, nxt;
} edges[M];
inline void addedge(int u, int v, int c)
{edges[idx] = {v, c, head[u]};head[u] = idx++;
}
inline void add(int u, int v, int c)
{addedge(u, v, c), addedge(v, u, 0);
}
bool bfs()
{memset(d, 0, sizeof(d));queue<int> q;q.emplace(s), d[s] = 1;while (q.size()){int u = q.front();q.pop();for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (!d[v] && edges[i].c){d[v] = d[u] + 1;q.emplace(v);if (v == t)return true;}}}return false;
}
int dfs(int u, int limit)
{if (u == t)return limit;int ret = 0;for (int i = cur[u]; ~i && limit; i = edges[i].nxt){cur[u] = i;int v = edges[i].v;if (d[v] == d[u] + 1 && edges[i].c){int incf = dfs(v, min(limit, edges[i].c));if (!incf)d[v] = 0;ret += incf, limit -= incf, edges[i].c -= incf, edges[i ^ 1].c += incf;}}return ret;
}
int dinic()
{int ret = 0;while (bfs())memcpy(cur, head, sizeof(head)), ret += dfs(s, inf);return ret;
}
int main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);freopen("in.txt", "r", stdin);cin >> m >> n;s = 0, t = m + n + 1;memset(head, -1, sizeof(head));int tot = 0;for (int i = 1; i <= m; i++){int r;cin >> r, add(s, i, r), tot += r;}for (int i = 1; i <= n; i++){int c;cin >> c, add(m + i, t, c);}for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)add(i, m + j, 1);if (dinic() != tot){cout << '0';}else{cout << '1' << '\n';for (int i = 1; i <= m; i++){for (int j = head[i]; ~j; j = edges[j].nxt)if (edges[j].v > m && edges[j].v <= m + n && !edges[j].c)cout << edges[j].v - m << ' ';cout << '\n';}}
}




)




)






)


