多臂老虎机理论系列

@[多臂老虎机理论](Lower bounds for non-adaptive exploration)

多臂老虎机之Lower bounds

定理 2.12：
在这里插入图片描述
定理的意义在于，对于任何不调整探索策略的算法，存在至少一个问题实例，使得随着时间的推移，该算法的预期遗憾将至少与 $T^{2/3}\times K^{1/3}$ 的乘积成比例增长。这表明，如果算法不采用基于过去经验调整其探索策略的自适应方法，那么在最坏情况下，它的性能会受到明显的限制。简而言之，这个定理强调了自适应探索在优化多臂老虎机问题中的重要性。
在这里插入图片描述
定理 2.12：建立在定理 2.11 的基础上，提出了一个更精细的下界。在定理 2.12 中，它假设了所有问题实例中，算法的预期遗憾的上界为 $\cdot T^\gamma$ ，其中 $\gamma\in[2/3,1)$ ，这意味着遗憾的增长速度慢于线性但快于 $T^{2/3}$ 。然而，定理指出即便如此，在最坏情况下，总遗憾的预期值仍然有一个较大的下界，具体为 $\mathbb{E}[R(T)] \geq \Omega (C^{-2} \cdot T^\lambda \cdot \sum_a \Delta(a)), \text{ where } \lambda = 2(1 - \gamma).$

这里的 $\Delta(a)$ 指的是某个臂 $a$ 的期望奖励与最佳臂之间的差距，而 $\sum_a \Delta(a)$ 就是所有臂的这种差距的总和。

文中提到的 Explore-first 策略，是一种先进行 N 轮探索的策略，其中 $N$ 是与 $\Delta^{-2} \log T$ 成正比的轮数。在这种情况下，如果问题实例的最小间隔至少为 $\Delta$ ，这种探索策略可以导致对数级别的遗憾增长，这在多臂老虎机问题中是一种非常有效的遗憾增长率。
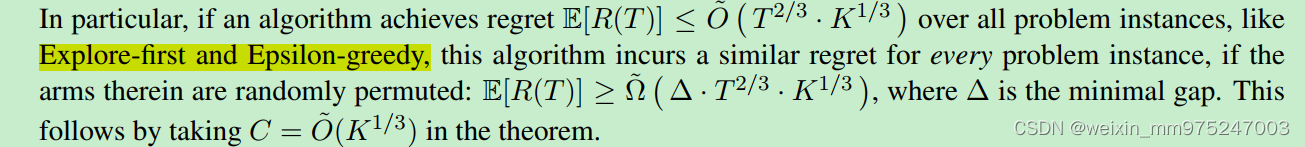
在这里插入图片描述

文中讨论了算法在多臂老虎机问题中的表现，特别是在所有问题实例上算法的遗憾上界和特定情况下的下界。
算法在所有问题实例上的遗憾上界： $\mathbb{E}[R(T)] \leq \tilde{O} (T^{2/3} \cdot K^{1/3})$ 。如果臂是随机排列的，算法在每个问题实例上的遗憾下界： $\mathbb{E}[R(T)] \geq \Omega (\Delta \cdot T^{2/3} \cdot K^{-1/3}),$

2.6 Instance-dependent lower bounds

在这里插入图片描述

这段文本提及的是多臂老虎机问题中的另一个基本下界。这里的下界是指算法在最优策略下所能实现的最小遗憾，这个下界依赖于实例的特定参数。文本中说的是，不同于 $\sqrt{KT}$ 这种对所有问题实例都适用的下界，存在一个与实例相关的常数，这个常数与 $\log(T)$ 相乘后给出了一个下界。这表明对于每一个问题实例，遗憾不能低于 $\Omega(\log(T))$ 的增长速度。这个下界补充了UCB1和Successive Elimination算法的 $\log(T)$ 上界。基本下界公式： $\Omega(\log(T)) \text{ regret}$ ，这个下界是对于所有问题实例都适用的，并且它强调了算法性能的一个重要限制——即使在最好的情况下，遗憾的增长速度也至少是对数级别的。
在这里插入图片描述
定理 2.13 表明没有算法能够达到预期遗憾小于 $o(c_T \log t)$ 对于所有问题实例 $I$ ，其中“常数” $c_T$ 可以依赖于问题实例但不依赖于时间 $t$ 。定理 2.13 指出，至少存在一个问题实例使得任何给定算法都有“高”遗憾。这个下界是对算法的一个限制，它说明在最佳情况下，算法的遗憾增长速度至少是对数级别的。作者提出要有一个更强的下界，确保每个问题实例都有高遗憾，但这是不可能的，因为总会有一些简单的策略在某些问题实例上表现得很好，即使这些策略看起来很“愚蠢”。例如，一个总是选择第一个臂的算法，在第一个臂是最佳的情况下遗憾为零。

为了排除这些反例，我们需要算法在所有问题实例上都表现得相对较好，即使它们不一定是最优的。
在这里插入图片描述
定理 2.14 为多臂老虎机问题中算法的遗憾提供了上界和下界。

上界表述如下：对于每个问题实例 $I$ 和每个 $\alpha > 0$ ，存在一个与问题实例和 $\alpha$ 相关，但与时间 $t$ 无关的常数 $C_{I,\alpha}$ ，使得算法的预期遗憾 $\mathbb{E}[R(t)]$ 满足 $\mathbb{E}[R(t)] \leq O(C_{I,\alpha} t^\alpha)$ 。这说明算法的性能不会随时间的推移无限下降；遗憾的增长有一个上限，该上限随时间的增长速度慢于 $t$ 的任意正实数次幂。

下界表述如下：对于任意固定的问题实例 $I$ ，存在一个时间点 $t_0$ ，使得对所有 $\geq t_0$ ，算法的预期遗憾满足 $\mathbb{E}[R(t)] \geq C_I \ln(t)$ ，这里的常数 $C_I$ 依赖于问题实例但不依赖于时间 $t$ 。这意味着随着时间的推移，算法的性能不能比对数增长的遗憾更好。

总的来说，定理 2.14 描述了多臂老虎机算法的一个性能界限，它告诉我们算法的遗憾随时间的增长是受限的，并且至少有对数级别的遗憾增长是不可避免的。这对于理解算法在长期运行中的表现具有重要意义。
在这里插入图片描述
该评论（Remark 2.15）提到了多臂老虎机算法性能的一个假设，并引入了如何根据臂的“间隙”来精细化定理 2.14。

Remark中提到的假设（Assumption 2.16）表明，如果一个算法的预期遗憾 $\mathbb{E}[R(t)]$ 小于等于 $log t)^{1000}$ ，那么它满足定理 2.14 中对预期遗憾的要求。

这个评论的意图是要进一步完善定理 2.14，特别是在如何选择与实例相关的常数 $C_I$ 上给出指导。这种精细化允许我们根据每个臂的间隙来调整算法的性能指标，以此提供一个更为个性化的遗憾界限，而不是使用一个普遍适用的常数。通过这样的方式，我们可以更精确地描述算法的长期性能，尤其是在面对不同难度的问题实例时。

简而言之，Remark 2.15 强调了在特定条件下，算法遗憾的界限可以进一步细化，并根据每个臂的间隙进行个性化调整。这有助于更好地理解算法在面对具有不同奖励结构的问题实例时的表现。

在这里插入图片描述

定理 2.16 给出了在多臂老虎机问题中，对于任何满足一定假设的算法的预期遗憾的两个不同界限的计算方法。

(a)部分 提供了一个界限，其中 $C_T$ 的值由所有臂的间隙 $\Delta(a)$ 的倒数加权的和决定，乘以最优臂的期望奖励 $\mu^*$ 和 $\mu^*)$ 的乘积：

$C_T = \sum_{a: \Delta(a)>0} \frac{\mu^*(1 - \mu^*)}{\Delta(a)}$
(b)部分 提供了另一个界限，适用于每个 $\varepsilon > 0$ ，这里 $C_T$ 是一个由臂的间隙 $\Delta(a)$ 和臂 $a$ 的期望奖励 $\mu(a)$ 与最优臂期望奖励 $\mu^*$ 之间的Kullback-Leibler散度的倒数加权的和，再减去一个小的正数 $\varepsilon$ ：

$C_T = \sum_{a: \Delta(a)>0} \frac{\Delta(a)}{KL(\mu(a), \mu^*)} - \varepsilon$

这些计算方法为算法在面对不同问题实例时，提供了量化的预期遗憾下界。

在这里插入图片描述
评论 2.17 对定理 2.14(a) 中的下界与两种特定算法的上界进行了比较。这两种算法是UCB1（Upper Confidence Bound 1）和Successive Elimination。

在多臂老虎机问题中，算法的目标是最小化遗憾，这是真实奖励与算法所选动作奖励之间的差值累计和。UCB1 和 Successive Elimination 都是尝试解决这个问题的算法。评论中提到的下界表示，即使在最优情况下，算法的遗憾也至少会按照某个和问题实例相关的对数因子增长。具体来说： $\leq \sum_{a: \Delta(a)>0} \frac{O(\log T)}{\Delta(a)}$ 这里的 $\Delta(a)$ 是指非最优臂 $a$ 与最优臂之间的期望奖励差值，而 $O(\log T)$ 表示遗憾增长的上界是对数级别的。这个下界是类似于UCB1和Successive Elimination算法遗憾增长的上界。

此外，评论还指出，当最优臂的期望奖励 $\mu^{*}$ 避开 0 和 1 的值时，上界是最优的，直到一个常数因子。例如，当 $\mu^*$ 的值在 $[1/4, 3/4]$ 的范围内时，上界被认为是最优的。这意味着，当最优臂的期望奖励既不是非常低也不是非常高时，这些算法提供的性能界限是紧的，即它们不能再被进一步提升。
在这里插入图片描述