牛客网---------[USACO 2016 Jan S]Angry Cows

题目描述

Bessie the cow has designed what she thinks will be the next big hit video game: "Angry Cows". The premise, which she believes is completely original, is that the player shoots cows with a slingshot into a one-dimensional scene consisting of a set of hay bales located at various points on a number line. Each cow lands with sufficient force to detonate the hay bales in close proximity to her landing site. The goal is to use a set of cows to detonate all the hay bales.

There are N hay bales located at distinct integer positions x1,x2,…,xN on the number line. If a cow is launched with power R landing at position x, this will causes a blast of "radius R", destroying all hay bales within the range x−R…x+R.

A total of K cows are available to shoot, each with the same power R. Please determine the minimum integer value of R such that it is possible to use the K cows to detonate every single hay bale in the scene.

输入描述:

The first line of input contains N (1≤N≤50,000) and K (1≤K≤10). The remaining N lines all contain integers x1…xN (each in the range 0…1,000,000,000).

输出描述:

Please output the minimum power R with which each cow must be launched in order to detonate all the hay bales.

示例1：

输入：

输出：

题目翻译：

奶牛贝西设计了一款她认为会成为下一个热门视频游戏的游戏:“愤怒的奶牛"。她认为这款游戏完全是原创的，游戏的前提是玩家用弹弓将奶牛射入一个由一组干草捆组成的一维场景中，这些干草捆位于一条数线上的不同点上。每头奶牛落地时都会产生足够的力量,以引爆着陆点附近的干草包。目标是用一组奶牛引爆所有干草包。有 N 个干草包，分别位于数线上不同的整数位置 x1、x2..xN。如果发射功率为R的奶牛落在x位置，就会产生"半径为 R"的爆炸，摧毁 [x-R，x+R] 范围内的所有干草包。请确定 R的最小整数值，以便能够用K头奶牛引爆场景中的每一个干草捆。

分析：

此题为二分答案，可以推出 r 越大，k 越小，具有单调性，所以我们小缩小距离，取找合适的炸弹数。

图解：

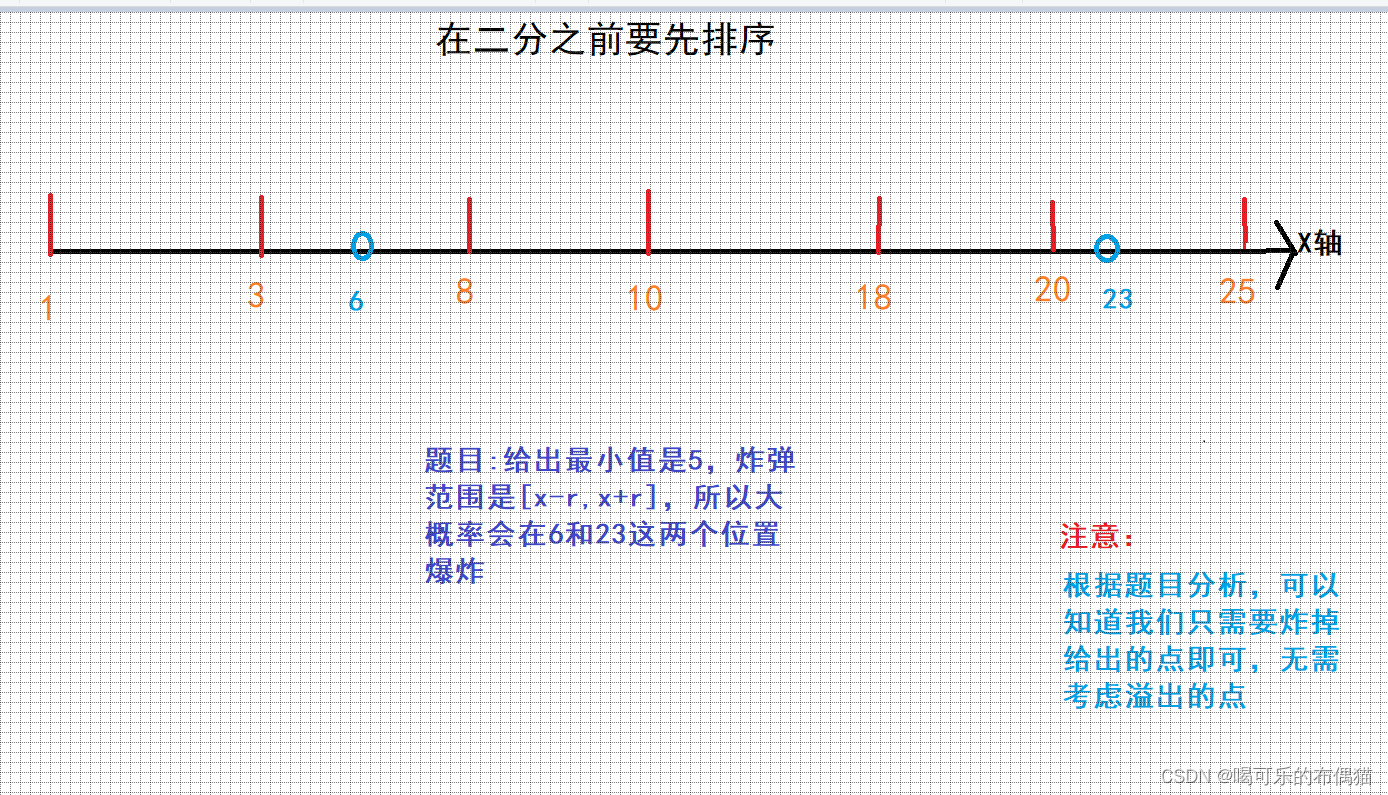
AC代码如下：

#include<iostream>
#include<algorithm>using namespace std;const int N = 50010;
int n,k,a[N];bool check(int x)
{int cow=0,last=0;for(int i=0;i<n;i++){if(a[i] - a[last] > 2*x){cow++; //扔一个牛炸弹//双指针算法 i在前走，j来保证(j,i)这个范围能被一个炸弹炸到（即：保证a[i]-a[j]<=2*mid）last = i; }//这里为什么要加1呢，举个例子 1 10 15//假如2*x=10,后面的15就空出来了，也不会执行cnt++,所以要+1。if(cow + 1 > k) return false;}return true;
}int main()
{scanf("%d %d",&n,&k);for(int i=0;i<n;i++) cin >> a[i];//用二分之前要先排好序sort(a,a+n);//这里就读好题，取好范围即可int l=0,r=1e9;//因为此题是求最小值，所以使用左面模板while(l < r){int mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << l;return 0;
}