题目

给定一个 正整数 数组 beans ，其中每个整数表示一个袋子里装的魔法豆的数目。

请你从每个袋子中 拿出 一些豆子（也可以 不拿出），使得剩下的 非空 袋子中（即 至少还有一颗 魔法豆的袋子）魔法豆的数目 相等。一旦把魔法豆从袋子中取出，你不能再将它放到任何袋子中。

请返回你需要拿出魔法豆的 最少数目。

示例

输入：beans = [4,1,6,5]
输出：4
解释：

• 我们从有 1 个魔法豆的袋子中拿出 1 颗魔法豆。
  剩下袋子中魔法豆的数目为：[4,0,6,5]
• 然后我们从有 6 个魔法豆的袋子中拿出 2 个魔法豆。
  剩下袋子中魔法豆的数目为：[4,0,4,5]
• 然后我们从有 5 个魔法豆的袋子中拿出 1 个魔法豆。
  剩下袋子中魔法豆的数目为：[4,0,4,4]

总共拿出了 1 + 2 + 1 = 4 个魔法豆，剩下非空袋子中魔法豆的数目相等。
没有比取出 4 个魔法豆更少的方案。

解析

这道题目题意上还是不太好理解的，最后要的结果是数组中的每个数据，要么是0，不为0的都应该相等。最后要求的是取出最少的豆子数目，转化一下求剩余最多的豆子。
解题思路第一步是先排序，从小到大排序，然后枚举排序后的数组，要求剩余的豆子最多，那就是剩余豆子组成的长方形面积最大，看下面这张图：

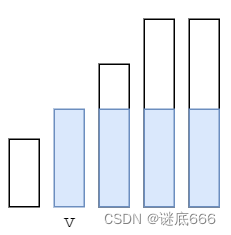
代码入下：

func minimumRemoval(beans []int) int64 {slices.Sort(beans)n := len(beans)sum := 0 // 总的面积maxArea := 0for i, v := range beans {sum += v // 总的豆子，用于最后计算剩余maxArea = max(maxArea , (n-i)*v) // 后面这个每个环节的矩形面积}return int64(sum - maxArea )
}