A - Scoreboard

Problem Statement

Team Takahashi and Team Aoki played $N$ matches.
In the $i$-th match $(1\le i\le N)$, Team Takahashi scored $X_i$ points, and Team Aoki scored $Y_i$ points.
The team with the higher total score from the $N$ matches wins.
Print the winner.
If the two teams have the same total score, it is a draw.

Constraints

$1\le N\le 100$
$0\le X_i\le 100(1\le i\le N)$
$0\le Y_i\le 100(1\le i\le N)$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$X_1$ $Y_1$
$X_2$ $Y_2$
$⋮$
$X_N$ $Y_N$

Output

If Team Takahashi wins, print Takahashi; if Team Aoki wins, print Aoki; if it is a draw, print Draw.

Sample Input 1

4
10 2
10 1
10 2
3 2

Sample Output 1

Takahashi

In four matches, Team Takahashi scored $33$ points, and Team Aoki scored $7$ points.
Team Takahashi wins, so print Takahashi.

Sample Input 2

6
5 4
4 5
2 4
1 6
7 1
3 2

Sample Output 2

Draw

Both teams scored $22$ points.
It is a draw, so print Draw.

Sample Input 3

4
0 0
10 10
50 50
0 100

Sample Output 3

Aoki

One or both teams may score no points in a match.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int N, X, Y, S1 = 0, S2 = 0;cin >> N;while (N --)cin >> X >> Y, S1 += X, S2 += Y;if (S1 == S2) puts("Draw");else if (S1 > S2) puts("Takahashi");else puts("Aoki");return 0;
}

B - Extended ABC

Problem Statement

We define Extended A strings, Extended B strings, Extended C strings, and Extended ABC strings as follows:
A string $S$ is an Extended A string if all characters in $S$ are A.
A string $S$ is an Extended B string if all characters in $S$ are B.
A string $S$ is an Extended C string if all characters in $S$ are C.
A string $S$ is an Extended ABC string if there is an Extended A string $S_A$, an Extended B string $S_B$, and an Extended C string $S_C$ such that the string obtained by concatenating $S_A,S_B,S_C$ in this order equals $S$.
For example, ABC, A, and AAABBBCCCCCCC are Extended ABC strings, but ABBAAAC and BBBCCCCCCCAAA are not.
Note that the empty string is an Extended A string, an Extended B string, and an Extended C string.
You are given a string $S$ consisting of A, B, and C.
If $S$ is an Extended ABC string, print Yes; otherwise, print No.

Constraints

$S$ is a string consisting of A, B, and C.
$1\le |S|\le 100$ ($|S|$ is the length of the string $S$.)

Input

The input is given from Standard Input in the following format:

$S$

Output

If $S$ is an Extended ABC string, print Yes; otherwise, print No.

Sample Input 1

AAABBBCCCCCCC

Sample Output 1

Yes

AAABBBCCCCCCC is an Extended ABC string because it is a concatenation of an Extended A string of length $3$, AAA, an Extended B string of length $3$, BBB, and an Extended C string of length $7$, CCCCCCC, in this order.
Thus, print Yes.

Sample Input 2

ACABABCBC

Sample Output 2

No

There is no triple of Extended A string $S_A$, Extended B string $S_B$, and Extended C string $S_C$ such that the string obtained by concatenating $S_A$, $S_B$, and $S_C$ in this order equals ACABABCBC.
Therefore, print No.

Sample Input 3

A

Sample Output 3

Yes

Sample Input 4

ABBBBBBBBBBBBBCCCCCC

Sample Output 4

Yes

Solution

具体见文后视频。

Code

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);string S;cin >> S;S.erase(unique(S.begin(), S.end()), S.end());if (S == "ABC" || S == "A" || S == "B" || S == "C" || S == "AB" || S == "AC" || S == "BC") puts("Yes");else puts("No");return 0;
}

C - Lining Up 2

Problem Statement

There are $N$ people standing in a line: person $1$, person $2$, $\dots$, person $N$.
You are given the arrangement of the people as a sequence $A=(A_1,A_2,\dots ,A_N)$ of length $N$.
$A_i(1\le i\le N)$ represents the following information:
if $A_i=-1$, person $i$ is at the front of the line;
if $A_i\ne -1$, person $i$ is right behind person $A_i$.
Print the people’s numbers in the line from front to back.

Constraints

$1\le N\le 3\times 10^5$
$A_i=-1$ or $1\le A_i\le N(1\le i\le N)$
There is exactly one way to arrange the $N$ people consistent with the information given.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$A_1$ $A_2$ $\dots$ $A_N$

Output

If person $s_1$, person $s_2$, $\dots$, person $s_N$ are standing in the line in this order, print $s_1$, $s_2$, $\dots$, and $s_N$ in this order, separated by spaces.

Sample Input 1

6
4 1 -1 5 3 2

Sample Output 1

3 5 4 1 2 6

If person $3$, person $5$, person $4$, person $1$, person $2$, and person $6$ stand in line in this order from front to back, the arrangement matches the given information.
Indeed, it can be seen that:
person $1$ is standing right behind person $4$,
person $2$ is standing right behind person $1$,
person $3$ is at the front of the line,
person $4$ is standing right behind person $5$,
person $5$ is standing right behind person $3$, and
person $6$ is standing right behind person $2$.
Thus, print $3$, $5$, $4$, $1$, $2$, and $6$ in this order, separated by spaces.

Sample Input 2

10
-1 1 2 3 4 5 6 7 8 9

Sample Output 2

1 2 3 4 5 6 7 8 9 10

Sample Input 3

30
3 25 20 6 18 12 26 1 29 -1 21 17 23 9 8 30 10 15 22 27 4 13 5 11 16 24 28 2 19 7

Sample Output 3

10 17 12 6 4 21 11 24 26 7 30 16 25 2 28 27 20 3 1 8 15 18 5 23 13 22 19 29 9 14

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 3e5 + 10;int N;
int A[SIZE], Next[SIZE];signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);memset(Next, -1, sizeof Next);cin >> N;for (int i = 1; i <= N; i ++){cin >> A[i];if (A[i] == -1) Next[0] = i;else Next[A[i]] = i;}for (int i = 0; Next[i] != -1; i = Next[i])cout << Next[i] << " ";return 0;
}

D - Cheating Gomoku Narabe

Problem Statement

There is a grid with $H$ rows and $W$ columns. Let $(i,j)$ denote the cell at the $i$-th row from the top and the $j$-th column from the left.
Each cell contains one of the characters o, x, and .. The characters written in each cell are represented by $H$ strings $S_1,S_2,\dots ,S_H$ of length $W$; the character written in cell $(i,j)$ is the $j$-th character of the string $S_i$.
For this grid, you may repeat the following operation any number of times, possibly zero:
Choose one cell with the character . and change the character in that cell to o.
Determine if it is possible to have a sequence of $K$ horizontally or vertically consecutive cells with o written in all cells (in other words, satisfy at least one of the following two conditions). If it is possible, print the minimum number of operations required to achieve this.
There is an integer pair $(i,j)$ satisfying $1\le i\le H$ and $1\le j\le W-K+1$ such that the characters in cells $(i,j),(i,j+1),\dots ,(i,j+K-1)$ are all o.
There is an integer pair $(i,j)$ satisfying $1\le i\le H-K+1$ and $1\le j\le W$ such that the characters in cells $(i,j),(i+1,j),\dots ,(i+K-1,j)$ are all o.

Constraints

$H$, $W$, and $K$ are integers.
$1\le H$
$1\le W$
$H\times W\le 2\times 10^5$
1 ≤ K ≤ max ⁡ { H , W } 1 \leq K \leq \max\lbrace H, W \rbrace 1≤K≤max{H,W}
$S_i$ is a string of length $W$ consisting of the characters o, x, and ..

Input

The input is given from Standard Input in the following format:

$H$ $W$ $K$
$S_1$
$S_2$
$⋮$
$S_H$

Output

If it is impossible to satisfy the condition in the problem statement, print -1. Otherwise, print the minimum number of operations required to do so.

Sample Input 1

3 4 3
xo.x
..o.
xx.o

Sample Output 1

2

By operating twice, for example, changing the characters in cells $(2,1)$ and $(2,2)$ to o, you can satisfy the condition in the problem statement, and this is the minimum number of operations required.

Sample Input 2

4 2 3
.o
.o
.o
.o

Sample Output 2

0

The condition is satisfied without performing any operations.

Sample Input 3

3 3 3
x..
..x
.x.

Sample Output 3

-1

It is impossible to satisfy the condition, so print -1.

Sample Input 4

10 12 6
......xo.o..
x...x.....o.
x...........
..o...x.....
.....oo.....
o.........x.
ox.oox.xx..x
....o...oox.
..o.....x.x.
...o........

Sample Output 4

3

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 2e5 + 10;int H, W, K;
int S1[SIZE], S2[SIZE];signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> H >> W >> K;char X;std::vector<vector<int>> G(H + 1, vector<int>(W + 1));for (int i = 1; i <= H; i ++)for (int j = 1; j <= W; j ++){cin >> X;if (X == 'x') G[i][j] = 0;else if (X == '.') G[i][j] = 1;else G[i][j] = 2;}int Result = 1e18;for (int i = 1; i <= H; i ++){for (int j = 1; j <= W; j ++)S1[j] = S1[j - 1] + (G[i][j] == 0), S2[j] = S2[j - 1] + (G[i][j] == 2);for (int j = K; j <= W; j ++)if (S1[j] - S1[j - K] == 0)Result = min(Result, K - S2[j] + S2[j - K]);}for (int i = 1; i <= W; i ++){for (int j = 1; j <= H; j ++)S1[j] = S1[j - 1] + (G[j][i] == 0), S2[j] = S2[j - 1] + (G[j][i] == 2);for (int j = K; j <= H; j ++)if (S1[j] - S1[j - K] == 0)Result = min(Result, K - S2[j] + S2[j - K]);}if (Result == 1e18) cout << -1 << endl;else cout << Result << endl;return 0;
}

E - Bad Juice

Problem Statement

This is an interactive problem (a type of problem where your program interacts with the judge program through Standard Input and Output).
There are $N$ bottles of juice, numbered $1$ to $N$. It has been discovered that exactly one of these bottles has gone bad. Even a small sip of the spoiled juice will cause stomach upset the next day.
Takahashi must identify the spoiled juice by the next day. To do this, he decides to call the minimum necessary number of friends and serve them some of the $N$ bottles of juice. He can give any number of bottles to each friend, and each bottle of juice can be given to any number of friends.
Print the number of friends to call and how to distribute the juice, then receive information on whether each friend has an upset stomach the next day, and print the spoiled bottle’s number.

Constraints

$N$ is an integer.
$2\le N\le 100$

Input/Output

This is an interactive problem (a type of problem where your program interacts with the judge program through Standard Input and Output).
Before the interaction, the judge secretly selects an integer $X$ between $1$ and $N$ as the spoiled bottle’s number. The value of $X$ is not given to you. Also, the value of $X$ may change during the interaction as long as it is consistent with the constraints and previous outputs.
First, the judge will give you $N$ as input.

$N$

You should print the number of friends to call, $M$, followed by a newline.

$M$

Next, you should perform the following procedure to print $M$ outputs.
For $i=1,2,\dots ,M$, the $i$-th output should contain the number $K_i$ of bottles of juice you will serve to the $i$-th friend, and the $K_i$ bottles’ numbers in ascending order, $A_{i,1},A_{i,2},\dots ,A_{i,K_i}$, separated by spaces, followed by a newline.

$K_i$ $A_{i,1}$ $A_{i,2}$ $\dots$ $A_{i,K_i}$

Then, the judge will inform you whether each friend has a stomach upset the next day by giving you a string $S$ of length $M$ consisting of 0 and 1.

$S$

For $i=1,2,\dots ,M$, the $i$-th friend has a stomach upset if and only if the $i$-th character of $S$ is 1.
You should respond by printing the number of the spoiled juice bottle $X^{\prime }$, followed by a newline.

$X^{\prime }$

Then, terminate the program immediately.
If the $M$ you printed is the minimum necessary number of friends to identify the spoiled juice out of the $N$ bottles, and the $X^{\prime }$ you printed matches the spoiled bottle’s number $X$, then your program is considered correct.

Notes

Each output should end with a newline and flushing Standard Output. Otherwise, you may receive a TLE verdict.
The verdict is indeterminate if your program prints an invalid output during the interaction or terminates prematurely. In particular, note that if a runtime error occurs during the execution of the program, the verdict may be WA or TLE instead of RE.
Terminate the program immediately after printing $X^{\prime }$. Otherwise, the verdict is indeterminate.
The judge for this problem is adaptive, meaning that the value of $X$ may change as long as it is consistent with the constraints and previous outputs.

Sample Input/Output

Below is an interaction with $N=3$.

Input	Output	Description
3		The number of bottles, $N$, is given.
	2	Print the number of friends to call, $M$.
	2 1 2	Serve juice $1$ and juice $2$ to the first friend.
	1 2	Serve juice $2$ to the second friend.
10		The string $S$ is given, indicating whether each friend has a stomach upset the next day.
	1	Print the spoiled bottle's number.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int N;cin >> N;int M = 0;while ((1ll << M) < N) M ++;cout << M << endl;for (int i = 0; i < M; i ++){std::vector<int> A;for (int j = 1; j <= N; j ++)if (j >> i & 1)A.push_back(j);cout << A.size() << " ";for (auto c : A) cout << c << " ";cout << endl;}string S;cin >> S;int Result = 0;for (int i = 0; i < M; i ++)if (S[i] == '1')Result += (1ll << i);if (Result == 0) cout << N << endl;else cout << Result << endl;return 0;
}

F - Usual Color Ball Problems

Problem Statement

You are given positive integers $N$, $M$, $K$, and a sequence of positive integers of length $N$, $(C_1,C_2,\dots ,C_N)$. For each $r=0,1,2,\dots ,N-1$, print the answer to the following problem.

There is a sequence of $N$ colored balls. For $i = 1, 2, \ldots, N$, the color of the $i$-th ball from the beginning of the sequence is $C_i$. Additionally, there are $M$ empty boxes numbered $1$ to $M$. Determine the total number of balls in the boxes after performing the following steps. First, perform the following operation $r$ times. Move the frontmost ball in the sequence to the end of the sequence. Then, repeat the following operation as long as at least one ball remains in the sequence. If there is a box that already contains at least one but fewer than $K$ balls of the same color as the frontmost ball in the sequence, put the frontmost ball into that box. If there is no such box, If there is an empty box, put the frontmost ball into the one with the smallest box number. If there are no empty boxes, eat the frontmost ball without putting it into any box.

## Constraints

All input values are integers.
$1\le N\le 2\times 10^5$
$1\le M,K\le N$
$1\le C_i\le N$

Input

The input is given from Standard Input in the following format:

$N$ $M$ $K$
$C_1$ $C_2$ $\dots$ $C_N$

Output

Print the answer $X_r$ to the problem for each $r=0,1,2,\dots ,N-1$ over $N$ lines as follows:

$X_0$
$X_1$
$⋮$
$X_{N-1}$

Sample Input 1

7 2 2
1 2 3 5 2 5 4

Sample Output 1

3
3
3
4
4
3
2

For example, let us explain the procedure for $r=1$.
First, perform the operation “Move the frontmost ball in the sequence to the end of the sequence” once, and the sequence of ball colors becomes $(2,3,5,2,5,4,1)$.
Then, proceed with the operation of putting balls into boxes as follows:
First operation: The color of the frontmost ball is $2$. There is no box with at least one but fewer than two balls of color $2$, so put the frontmost ball into the empty box with the smallest box number, box $1$.
Second operation: The color of the frontmost ball is $3$. There is no box with at least one but fewer than two balls of color $3$, so put the frontmost ball into the empty box with the smallest box number, box $2$.
Third operation: The color of the frontmost ball is $5$. There is no box with at least one but fewer than two balls of color $5$ and no empty boxes, so eat the frontmost ball.
Fourth operation: The color of the frontmost ball is $2$. There is a box, box $1$, with at least one but fewer than two balls of color $2$, so put the frontmost ball into box $1$.
Fifth operation: The color of the frontmost ball is $5$. There is no box with at least one but fewer than two balls of color $5$ and no empty boxes, so eat the frontmost ball.
Sixth operation: The color of the frontmost ball is $4$. There is no box with at least one but fewer than two balls of color $4$ and no empty boxes, so eat the frontmost ball.
Seventh operation: The color of the frontmost ball is $1$. There is no box with at least one but fewer than two balls of color $1$ and no empty boxes, so eat the frontmost ball.
The final total number of balls in the boxes is $3$, so the answer to the problem for $r=1$ is $3$.

Sample Input 2

20 5 4
20 2 20 2 7 3 11 20 3 8 7 9 1 11 8 20 2 18 11 18

Sample Output 2

14
14
14
14
13
13
13
11
8
9
9
11
13
14
14
14
14
14
14
13

Solution

这题没研究，就不写了

---

Code

G - Tree Inversion

Problem Statement

You are given a tree $T$ with $N$ vertices: vertex $1$, vertex $2$, $\dots$, vertex $N$.
The $i$-th edge $(1\le i<N)$ connects vertices $u_i$ and $v_i$.
For a vertex $u$ in $T$, define $f(u)$ as follows:
$f(u):=$ The number of pairs of vertices $v$ and $w$ in $T$ that satisfy the following two conditions:
Vertex $w$ is contained in the path connecting vertices $u$ and $v$.
$v<w$.
Here, vertex $w$ is contained in the path connecting vertices $u$ and $v$ also when $u=w$ or $v=w$.
Find the values of $f(1),f(2),\dots ,f(N)$.

Constraints

$2\le N\le 2\times 10^5$
$1\le u_i\le N(1\le i\le N)$
$1\le v_i\le N(1\le i\le N)$
The given graph is a tree.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$u_1$ $v_1$
$u_2$ $v_2$
$⋮$
$u_{N-1}$ $v_{N-1}$

Output

Print the values of $f(1),f(2),\dots ,f(N)$ in this order, separated by spaces.

Sample Input 1

7
1 2
2 3
2 4
4 5
4 6
6 7

Sample Output 1

0 1 3 4 8 9 15

The given tree is as follows:

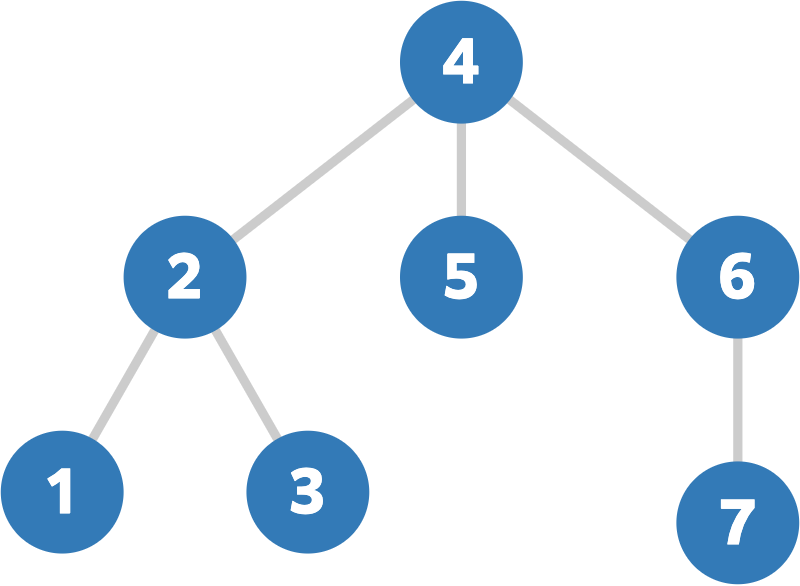
For example, $f(4)=4$.
Indeed, for $u=4$, four pairs $(v,w)=(1,2),(1,4),(2,4),(3,4)$ satisfy the conditions.

Sample Input 2

15
14 9
9 1
1 6
6 12
12 2
2 15
15 4
4 11
11 13
13 3
3 8
8 10
10 7
7 5

Sample Output 2

36 29 32 29 48 37 45 37 44 42 33 36 35 57 35

The given tree is as follows:

The value of $f(14)$ is $57$, which is the inversion number of the sequence $(14,9,1,6,12,2,15,4,11,13,3,8,10,7,5)$.

Sample Input 3

24
7 18
4 2
5 8
5 15
6 5
13 8
4 6
7 11
23 16
6 18
24 16
14 21
20 15
16 18
3 16
11 10
9 11
15 14
12 19
5 1
9 17
5 22
11 19

Sample Output 3

20 20 41 20 21 20 28 28 43 44 36 63 40 46 34 40 59 28 53 53 66 42 62 63

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define lowbit(x) x & -x
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 2e5 + 10;int N;
std::vector<int> G[SIZE];
int DFS_Order[SIZE], Id = 0, Sz[SIZE];
int Count[SIZE], Pos[SIZE];
int Root[SIZE], idx, Answer[SIZE];
struct Node
{int l, r;int cnt;
}Tree[SIZE * 21];int Build(int l, int r)
{int p = ++ idx;if (l == r) return p;int mid = l + r >> 1;Tree[p].l = Build(l, mid), Tree[p].r = Build(mid + 1, r);return p;
}int Insert(int p, int l, int r, int x)
{int q = ++ idx;Tree[q] = Tree[p];if (l == r){Tree[q].cnt ++;return q;}int mid = l + r >> 1;if (x <= mid) Tree[q].l = Insert(Tree[p].l, l, mid, x);else Tree[q].r = Insert(Tree[p].r, mid + 1, r, x);Tree[q].cnt = Tree[Tree[q].l].cnt + Tree[Tree[q].r].cnt;return q;
}int Query(int q, int p, int l, int r, int k)
{int Cnt = Tree[Tree[q].l].cnt - Tree[Tree[p].l].cnt;if (l == r) return Tree[q].cnt - Tree[p].cnt;int mid = l + r >> 1;if (k <= mid) return Query(Tree[q].l, Tree[p].l, l, mid, k);else return Cnt + Query(Tree[q].r, Tree[p].r, mid + 1, r, k);
}struct Segment
{struct Node{int l, r;LL Sum, Lazy;}Tree[SIZE << 2];void Pushup(int u) { Tree[u].Sum = Tree[u << 1].Sum + Tree[u << 1 | 1].Sum; }void Pushdown(int u){if (Tree[u].Lazy){Tree[u << 1].Sum += (LL)(Tree[u << 1].r - Tree[u << 1].l + 1) * Tree[u].Lazy;Tree[u << 1].Lazy += Tree[u].Lazy;Tree[u << 1 | 1].Sum += (LL)(Tree[u << 1 | 1].r - Tree[u << 1 | 1].l + 1) * Tree[u].Lazy;Tree[u << 1 | 1].Lazy += Tree[u].Lazy;Tree[u].Lazy = 0;}}void Build(int u, int l, int r){Tree[u] = {l, r};if (l == r) return;int mid = l + r >> 1;Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);}void Modify(int u, int l, int r, int d){if (Tree[u].l >= l && Tree[u].r <= r){Tree[u].Sum += (LL)(Tree[u].r - Tree[u].l + 1) * d;Tree[u].Lazy += d;return;}Pushdown(u);int mid = Tree[u].l + Tree[u].r >> 1;if (mid >= l) Modify(u << 1, l, r, d);if (mid < r) Modify(u << 1 | 1, l, r, d);Pushup(u);}long long Query(int u, int l, int r){if (Tree[u].l >= l && Tree[u].r <= r)return Tree[u].Sum;Pushdown(u);long long mid = Tree[u].l + Tree[u].r >> 1, Result = 0;if (mid >= l) Result = Query(u << 1, l, r);if (mid < r) Result += Query(u << 1 | 1, l, r);return Result;}
}Result;void DFS(int u, int fa)
{Sz[u] = 1;for (auto c : G[u]){if (c == fa) continue;DFS_Order[ ++ Id] = c, Pos[c] = Id;DFS(c, u);Sz[u] += Sz[c];}
}
void DFS2(int u, int fa)
{for (auto c : G[u]) { if (c == fa) continue; DFS2(c, u); }int C1 = Query(Root[Pos[u] + Sz[u] - 1], Root[Pos[u] - 1], 1, N, u);// cout << u << ":" << Pos[u] << " " << Pos[u] + Sz[u] - 1 << " " << C1 << endl;if (Pos[u] > 1) Result.Modify(1, 1, Pos[u] - 1, C1 - 1);if (Pos[u] + Sz[u] <= N) Result.Modify(1, Pos[u] + Sz[u], N, C1 - 1);Result.Modify(1, Pos[u], Pos[u] + Sz[u] - 1, u - C1);for (auto c : G[u]){if (c == fa) continue;int C2 = Query(Root[Pos[c] + Sz[c] - 1], Root[Pos[c] - 1], 1, N, u);// cout << u << " " << c << " " << C2 << endl;if (Pos[u] <= Pos[c] - 1) Result.Modify(1, Pos[u], Pos[c] - 1, C2);if (Pos[c] + Sz[c] <= Pos[u] + Sz[u] - 1) Result.Modify(1, Pos[c] + Sz[c], Pos[u] + Sz[u] - 1, C2);}
}bool Cmp(PII A, PII B) { return A.second < B.second; }signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> N;int u, v;for (int i = 1; i < N; i ++)cin >> u >> v, G[u].push_back(v), G[v].push_back(u);Result.Build(1, 1, N);DFS_Order[ ++ Id] = 1, Pos[1] = Id;DFS(1, -1);// for (int i = 1; i <= N; i ++)// 	cout << DFS_Order[i] << " ";// cout << endl;Root[0] = Build(1, N);for (int i = 1; i <= N; i ++)Root[i] = Insert(Root[i - 1], 1, N, DFS_Order[i]);DFS2(1, -1);for (int i = 1; i <= N; i ++)Answer[DFS_Order[i]] = Result.Query(1, i, i);for (int i = 1; i <= N; i ++)cout << Answer[i] << " ";return 0;
}

视频题解

---

最后祝大家早日