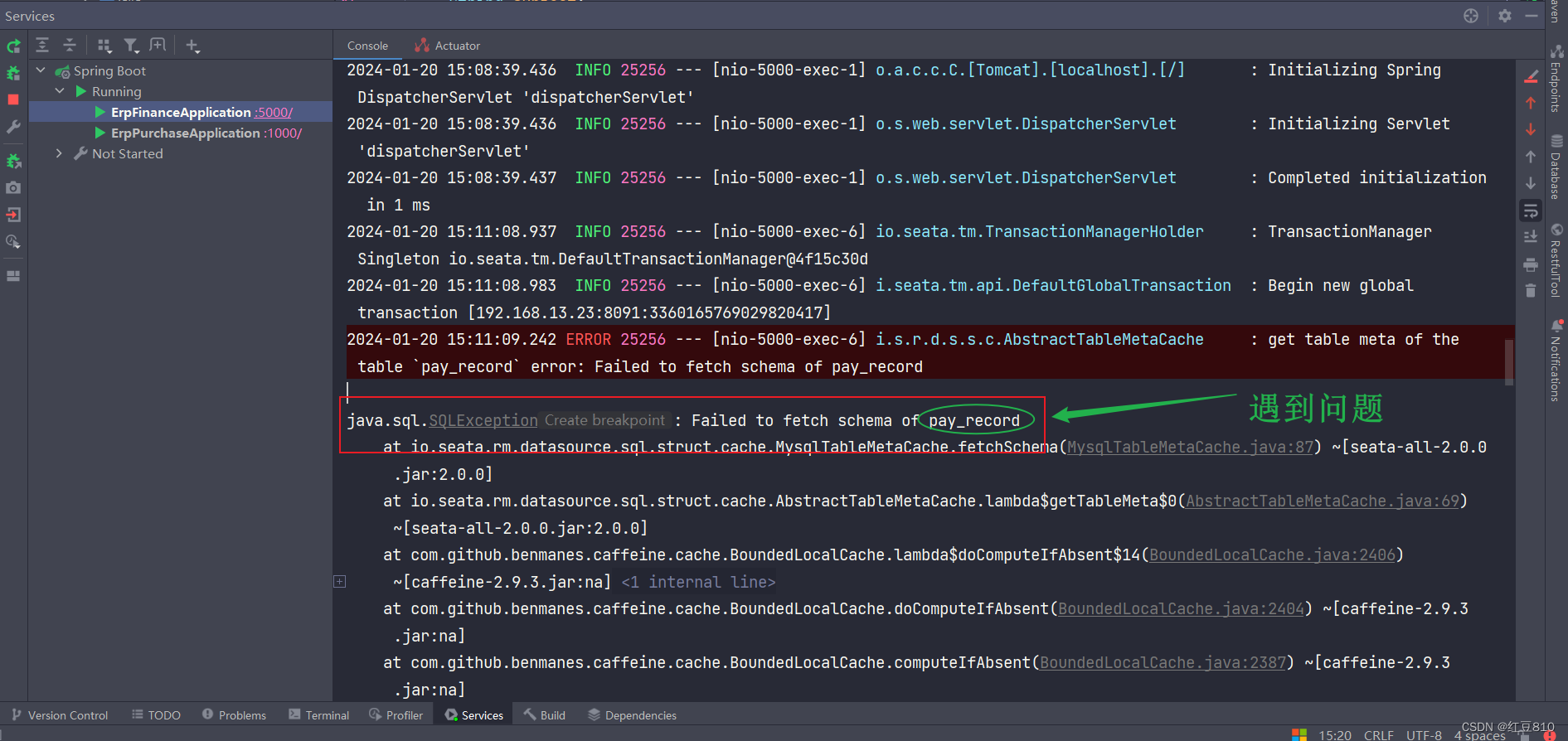
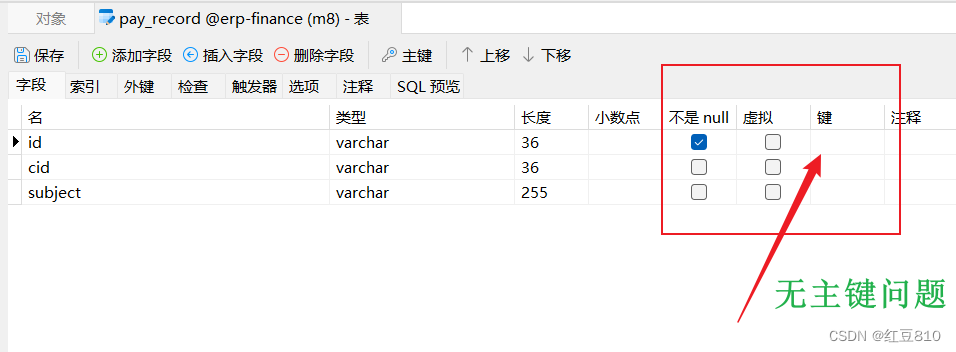
java.sql.SQLException: Failed to fetch schema of XXX 问题
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/635913.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
上海亚商投顾:沪指冲高回落 旅游板块全天强势
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪
沪指昨日冲高回落,创业板指跌近1%,北证50指数跌超3%。旅游、零售板块全天强势…
200. 岛屿数量(js)
示例 1:
输入:grid [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"…
Angular 表单的validation校正学习
概念: Angular中的表单valid是指表单中的输入项是否符合预设的规则和条件。在Angular中,可以通过使用表单控件的属性和方法来判断表单的valid状态,例如使用form.valid属性来判断整个表单是否valid,或者使用formControl.valid属性来…
记自动化测试发现的一个因表空间不足引发的BUG
0 背景介绍 这是一个BS架构的项目,数据库是SQL Server,前端浏览器呈现数据,操作数据。 1 现象介绍 功能为发送消息,类似广播,相关人员在系统中都可以接收到。之前功能都正常,这两天跑自动化测试时&#x…
python类继承之__init__函数覆盖问题
目录
1.问题描述
2.代码演示
3.总结 在Python这个广受欢迎的编程语言中,类继承是一项强大而精巧的特性。通过类继承,我们可以构建出更加灵活、可重用和易维护的代码,同时实现代码的模块化和扩展性。
但是如果对于熟悉C和java的人而言&…
R语言学习 case2:人口金字塔图
step1:导入库
library(ggplot2)
library(ggpol)
library(dplyr)step2:读取数据
data <- readxl::read_xlsx("data_new.xlsx", sheet 1)
datareadxl::read_xlsx() 是 readxl 包中的函数,用于读取Excel文件。
step3࿱…
ckman:非常好用的ClickHouse可视化集群运维工具
概述
什么是ckman
ckman,全称是ClickHouse Management Console, 即ClickHouse管理平台。它是由擎创科技数据库团队主导研发的一款用来管理和监控ClickHouse集群的可视化运维工具。目前该工具已在github上开源,开源地址为:github…
全网最详细丨2024年AMC8真题及答案来了
目录 前言
真题回忆
真题解析
结尾 前言
相信大家都已经知道今年AMC8出事情了吧,但最重要的还是要从中学到新知识。
听说今年考生被提前12分钟强制交卷了,肯定因为试题泄露了。
最新回复:我们这边已经退费了
真题回忆 需要word文档的请…
计算机网络基础概念解释
1. 什么是网络
随着时代的发展,越来越需要计算机之间互相通信,共享软件和数据,即以多个计算机协同⼯作来完成业务,于是有了网络互连。 网络互连:将多台计算机连接在⼀起,完成数据共享。 数据共享本质是网络…
Android System Service系统服务--1
因为工作中经常需要解决一些framework层的问题,而framework层功能一般都是system service 的代理stub,然后封装相关接口,并提供给APP层使用,system service则在不同的进程中运行,这样实现了分层,隔离&#…
「 网络安全常用术语解读 」杀链Kill Chain详解
1. 简介
早在2009年,Lockheed Martin公司就提出了杀链(Kill Chain)理论,现在也称之为攻击者杀链(Attacker Kill Chain)。杀链其实就是攻击者进行网络攻击时所采取的步骤。杀链模型包括7个步骤:1侦察 -> 2武器化 -> 3交付 -> 4利用 …
不要长期把焦点放在让你烦恼的事情上
不要长期把焦点放在让你烦恼的事情上
在快节奏的生活中,我们经常会遇到各种各样让我们担心的事情。这些事情可能是工作上的压力,家庭中的矛盾,或者是个人的迷茫和困惑。然而,长期将焦点放在这些让我们烦恼的事情上,不…
PrestaShop购物系统 SQL注入漏洞复现(CVE-2023-30150)
0x01 产品简介
PrestaShop 是一个功能丰富,基于 PHP5 开发的 Web2.0 网上购物系统。PrestaShop 具有可定制,稳定等特点。整个系统只有 5.8MB,易于快速安装。
0x02 漏洞概述
PrestaShop 的部分主题中使用Leo Custom Ajax模块拓展,Leo Custom Ajax模块中可以在/modules/le…
JNPF低代码开发平台
一、关于低代码 JNPF平台在提供无代码(可视化建模)和低代码(高度可扩展的集成工具以支持跨功能团队协同工作)开发工具上是独一无二的。支持简单、快速地构建及不断改进Web端应用程序,可为整个应用程序的生命周期提供全…
HarmonyOS鸿蒙学习基础篇 - 项目目录和文件介绍
├── hvigor //存储购置信息的文件,主要用于发布打包
├── idea //开发工具相关配置可忽略
├── AppScope //工程目录 全局公共资源存放路径
│ └── resources
│ │ └── base
│ │ │ └── element //常亮存放
│ │ │ …
beego项目部署与热更新
1.开发自己的第一个项目
这里我引用的是在线聊天室,参考源码是https://github.com/beego/samples/tree/master/WebIM
在源码的基础上重新开发,整理项目发布到了liu289747235/WebIM
推荐下载源码:https://gitee.com/myselfyou/web-im
在线…
2023年12月青少年软件编程Python等级考试(六级)真题试卷
2023年12月青少年软件编程Python等级考试(六级)真题试卷 单选题 第 1 题 单选题 运行以下程序,输出的结果是?( )
class A(): def __init__(self,x): self.xx1 def b(self): re…
游戏开发中的噪声算法
一、噪声 噪声是游戏编程的常见技术,广泛应用于地形生成,图形学等多方面。 那么为什么要引入噪声这个概念呢?在程序中,我们经常使用直接使用最简单的rand()生成随机值,但它的问题在于生成的随机值太“随机”了…
爬虫之牛刀小试(八):爬取微博评论
今天爬取的是微博评论。 可以发现其特点是下一页评论的max_id在上一页中。 于是代码如下: import requests
import json
import re
import time
headers {User-Agent: ,"Cookie": "","Referer": "https://m.weibo.cn/detail/4…

)











)



真题试卷)

:爬取微博评论)