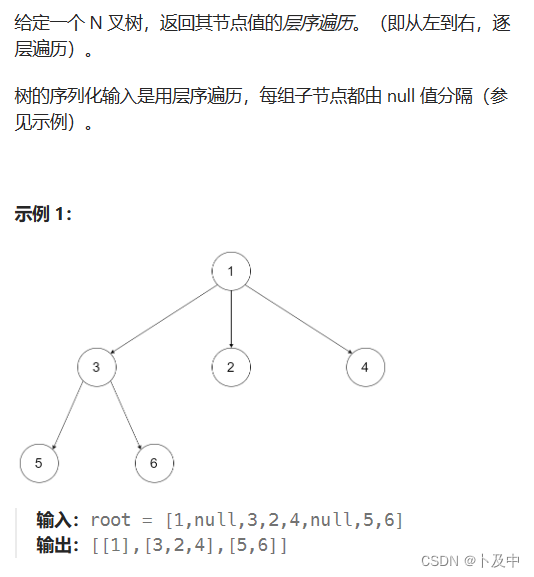
思路

• 解法：队列，宽度优先搜索
  

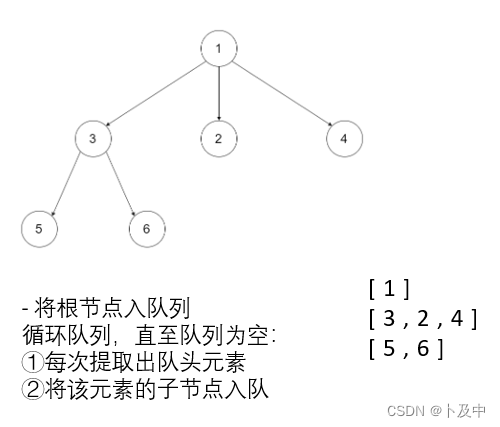
  1. 如上图所写，首先将根节点入队
  2. 循环队列，直至队列为空：
     3. q.size即为该层节点数，循环q.size次：提取出队头节点，并将该节点的所有子节点入队
  3. 每遍历一层，将结果加入到结果数组ret中

代码

vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret; // 最终结果queue<Node*> q; // 用队列记录节点// 将本层元素放入队列，提取出值后出队，将子节点入队if(root) q.push(root);else    return ret;while(q.size()){int sz = q.size(); // 记录本层元素个数vector<int> tmp; // 用于存储本层元素值for(int i = 0; i < sz; ++i){Node* t = q.front();q.pop();tmp.push_back(t->val); // tmp记录该层节点值for(Node* child : t->children) // 当前节点的子节点入队{if(child) // 不为空q.push(child);}}ret.push_back(tmp); // 更新结果}return ret;
}

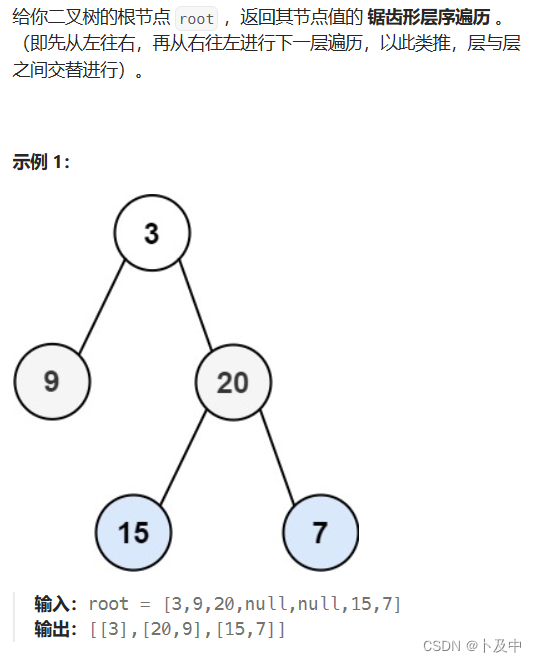
思路

• 题意分析：要求按照先从左往右进行一层遍历、再从左往右进行下一层遍历，重复遍历完二叉树
  • 我们可以将其理解为奇数层正序遍历（从左向右），偶数层逆序遍历
• 解法：队列，宽度优先搜索
• 该题与上一道很类似，只需要添加一个遍历用于标记当前层为奇数还是偶数，用于判断逆序还是正序
  1. 使用一个队列来存储当前层的所有节点，同时记录当前层的节点数。
  2. 依次从队列中取出节点，将其值加入到当前层的结果集tmp中，并将其左右子节点加入队列中。
  3. 如果当前层为偶数层，则需要将tmp逆序后再加入到结果集ret中。
  4. 最后返回结果集ret。

代码

vector<vector<int>> zigzagLevelOrder(TreeNode* root) {// 锯齿形层序遍历：偶数层逆序遍历，奇数层正常遍历vector<vector<int>> ret;queue<TreeNode*> q;if(!root) return ret;else q.push(root);int level = 1; // 根据flag判断是否逆序while(q.size()){int sz = q.size(); // 记录本层个数vector<int> tmp;for(int i = 0; i < sz; ++i){TreeNode* t = q.front();q.pop();tmp.push_back(t->val);if(t->left) q.push(t->left);if(t->right) q.push(t->right);}if(level % 2 == 0)   reverse(tmp.begin(), tmp.end());ret.push_back(tmp);++level;}return ret;
}

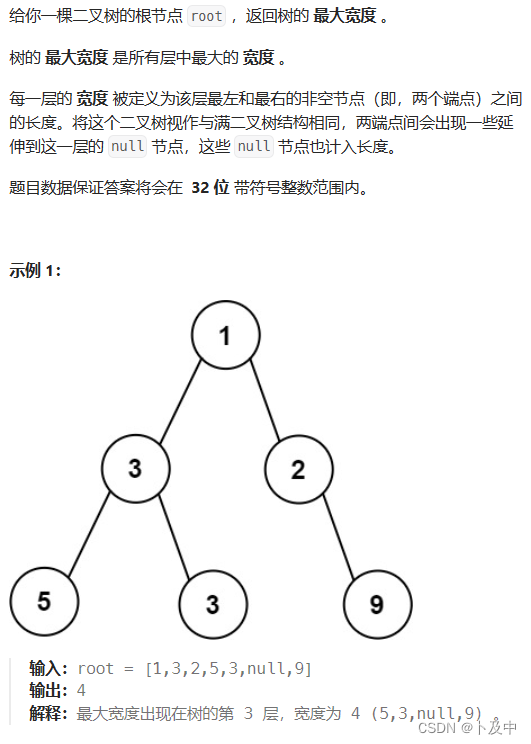
思路

• 题意分析：即返回二叉树的最大宽度，即最大层的宽度
• 解法：记录节点下标、数组表示队列
  
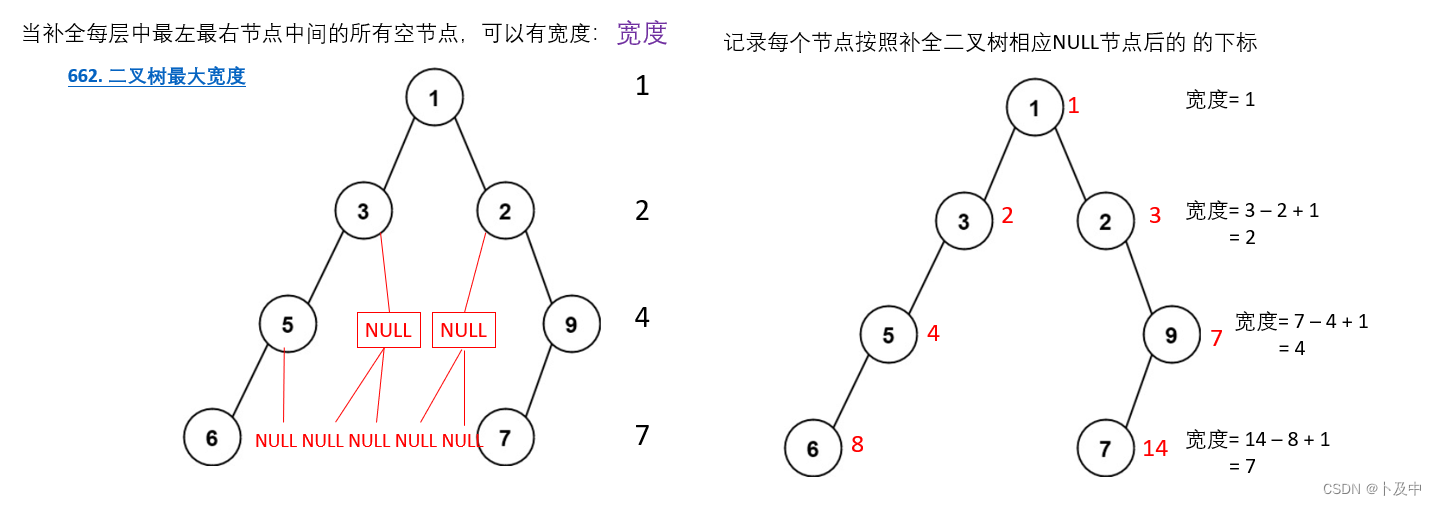
  • 如上图的思路，我们用数组表示队列，队列中存放pair类型，分别为节点和其对应的下标
  1. 将根节点及其下标1插入队列，进行循环，直至队列为空
  2. 提取队尾和队头两元素（即为该层的最左最有的节点）并记录 / 更新结果
  3. 将该层的所有子节点入队
  4. 最后返回结果ret

代码

int widthOfBinaryTree(TreeNode* root) {// 队列（数组）存储节点及其下标（补全null节点后的下标）vector<pair<TreeNode*, unsigned int>> q;// q.push_back(make_pair<nullptr, 0>); if(!root) return 0;else q.push_back({root, 1}); // // 根节点从1下标开始unsigned int ret = 0; // 最终结果while(q.size()){// 计算本层宽度auto [node1, x1] = q[0]; // 提取一个pair类型auto [node2, x2] = q.back();ret = max(ret, x2 - x1 + 1);vector<pair<TreeNode*, unsigned int>> tmp; // tmp存储下一层节点信息，覆盖qfor(auto& [node, x] : q){// 左孩子下标：2x 右孩子下标:2x+1if(node->left) tmp.push_back({node->left, 2*x});if(node->right) tmp.push_back({node->right, 2*x + 1});}q = tmp;}return ret;
}

思路

• 解法：队列 + 层序遍历
• 直接利用队列队树进行层序遍历即可
• 每层循环定义一次变量maxVal用于寻找最大值

代码

vector<int> largestValues(TreeNode* root) {vector<int> ret; // 结果数组queue<TreeNode*> q; // 队列用于层序遍历if(!root) return ret;else q.push(root);while(!q.empty()){int sz = q.size();int maxVal = INT_MIN; // 用于比较节点大小 while(sz--){auto t = q.front(); // 提取当前节点q.pop();maxVal = max(maxVal, t->val);if(t->left) q.push(t->left);if(t->right) q.push(t->right);}ret.push_back(maxVal);}return ret;
}