实验2 概率与分布
一、实验目的
1. 掌握理解离散型概率分布的相关概念。
2. 掌握理解连续型概率分布的相关概念。
3. 熟悉R语言等语言的集成开发环境。
二、实验分析与内容
完成教材P52-53的第2题和第8题
2.一条食品生产线每8小时一班中出现故障的次次数服从平均值为1.5的泊松分布。求:
(1)晚班期间恰好发生两次事故的概率
> lambda=1.5
> dpois(2,lambda)
[1] 0.2510214
（2）下午班期间发生少于两次事故的概率。
> dpois(0:1,lambda)
[1] 0.2231302 0.3346952
> dpois(0,lambda)+dpois(1,lambda)
[1] 0.5578254
（3）连续三班无故障的概率。
> dpois(0,lambda)*dpois(0,lambda)*dpois(0,lambda)
[1] 0.011109
某企业生产的某种电池寿命近似服从正态分布,且均值为200小时，标准差为30小时。若规定寿命低于150小时为不合格品。
- 该企业所生产电池的合格率是多少?
> 1-pnorm(150,mean=200,sd=30)
[1] 0.9522096
- 电池寿命在200小时左右多大范围内的概率不小于0.9?
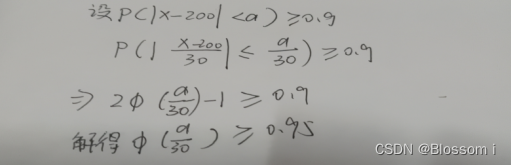
三、实验总结
在本次实验加深了对解离散型概率分布泊松分布以及连续型概率分布正态分布的相关概念，并用R语言开发环境来实现离散型概率分布泊松分布以及连续型概率分布正态分布的题目实现过程。
题目一：在R中，pois表示泊松分布，加上不同的前缀表示不同的函数，加上前缀d表示概率密度函数，加上前缀p表示分布函数，加前缀q表示分位函数，加前缀r表示随机生成数，各函数的语法格式如下：其中x变量表示服从泊松分布函数的成功的次数，而均值表示数量的均值(此处均值mean= lambda)
dpois( x, lambda, log = FALSE ) #发生x次随机事件的概率ppois( q, lambda, lower.tail = TRUE, log.p = FALSE ) # 至多发生q次事件的累计概率qpois( p, lambda, lower.tail = TRUE, log.p = FALSE ) #在p概率下事件发生的次数rpois( n, lambda ) #重复n组试验，每组发生随机事件的次数
本次实验题目一是用函数dpois（x，mean）
题目二：题目中提到是连续型概率分布的正态分布。
在R中，rnorm（x，mean，sd）函数来随机抽取正太分布随机数，只是抽取符合正态分布的随机数。dnorm（x，mean，sd）函数为正态分布的概率密度函数。pnorm（x，mean，sd）函数， Probability的缩写，表示概率函数。qnorm（x，mean，sd）函数 Quantile的缩写，表示分位函数
本题用pnorm（x，mean，sd）函数和pnorm（x，mean，sd）函数,x变量，mean均值，sd标准差。对题目进行数学分析，巧妙运用函数得出题目所要求的内容。
在本次实验中学习理解了离散型概率分布泊松分布以及连续型概率分布正态分布的函数，但还没有达到非常熟练的程度，还需要加强学习。
