案例背景
本次案例是博主本科在行为金融学课程上做的一个小项目,最近看很多经管类的学生作业都很需要,我就用python来重新做了一遍。不弄那些复杂的机器学习模型了,经管类同学就用简单的统计学方法来做模型就好。
研究目的
有效市场假说是现代金融证券市场的理论基础之一,根据这一理论,投资者买卖股票市场是很难通过主动管理去获得超额收益,而且平均时间段的收益应该也没有显著性的差异。
但在我国市场明显存在着一个春节效应,即股市二月份的收益率一般远要高于一年中其他月份的收益率。而且中国股市还有一句老话,叫做五穷六绝七翻身,意思是五月六月的收益率低,而七月的收益率就有所上升。国外学者研究中,一些成熟的股票市场也会出现着这样一种季节性的或是周末性的效应。这种违背了有效市场假说的现象,一般应该与人的心理会有联系,研究范围属于行为金融学范围。
本文以上证综合指数为例,选取收盘价作为样本数据,对其进行实证分析研究,检验中国股市是否呈现在了月份效应,根据这一分析,可以对股票投资策略上提出一定的建议。
数据
既然研究中国股市,那就用最有代表性的A股上证指数吧,十多年了还是3000点不保.....
使用akshare的api接口进行获取数据,当然本项目的全部代码和数据文件还是可以这样获取,需要的同学可以看看:数据
代码实现
导入包:
import akshare as ak
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns %matplotlib inline
plt.rcParams['font.sans-serif'] = ['KaiTi'] #中文
plt.rcParams['axes.unicode_minus'] = False #负号数据获取
然后获取上证指数的数据
# 获取上证指数的日K线数据
df_300= ak.stock_zh_index_daily(symbol="sh000001")
df_300 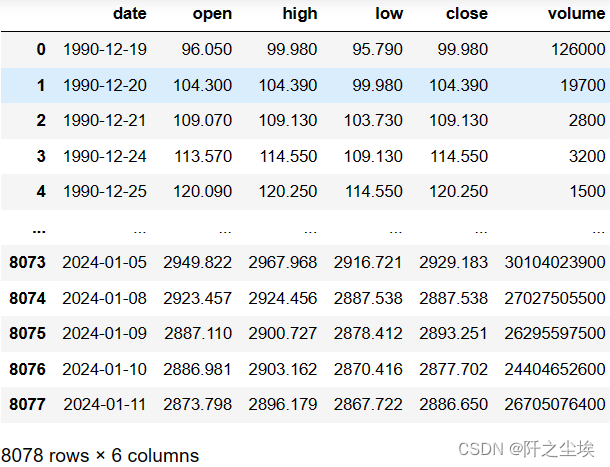
##储存
df_300.to_excel('data.xlsx',index=False)换成别的数据文件都可以,别的股票或者指数....
数据转化
要换成自己的数据文件就再读取一遍就好了,命名为df_300,后面一样用。
既然研究月份,那么得需要先计算每个月的收益率,转化日K为月份
# 转换日期格式并设置为索引
df_300['date'] = pd.to_datetime(df_300['date'])
df_300.set_index('date', inplace=True)
df=df_300.resample('M').ffill()使用每个月的收盘价
df['monthly_return']=df['close'].pct_change().fillna((0))
df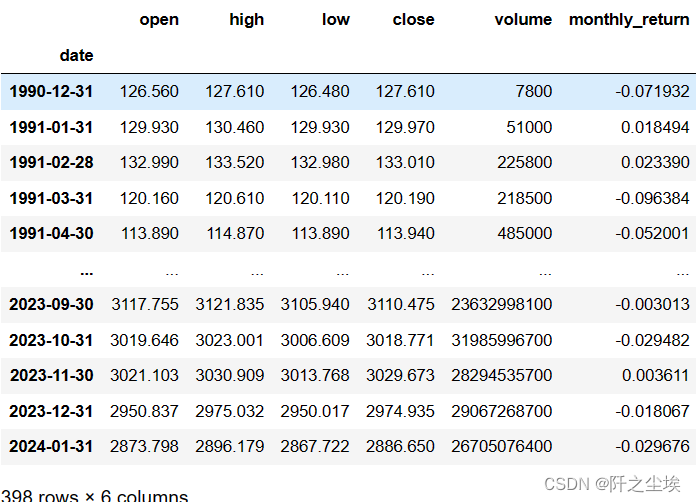
最后一列就是每个月的收益率了,但是这样一条数据不直观,这样看比较好:
data=pd.DataFrame()
data['monthly_return']=df['monthly_return']
data['year'] = df.index.year
data['month'] = df.index.month
data = data.pivot_table(index='year', columns='month', values='monthly_return').iloc[1:-1,:]
data
这样就可以清楚地看见每年每个月的收益率了。
描述性统计
描述性统计也很方便:
data.describe() 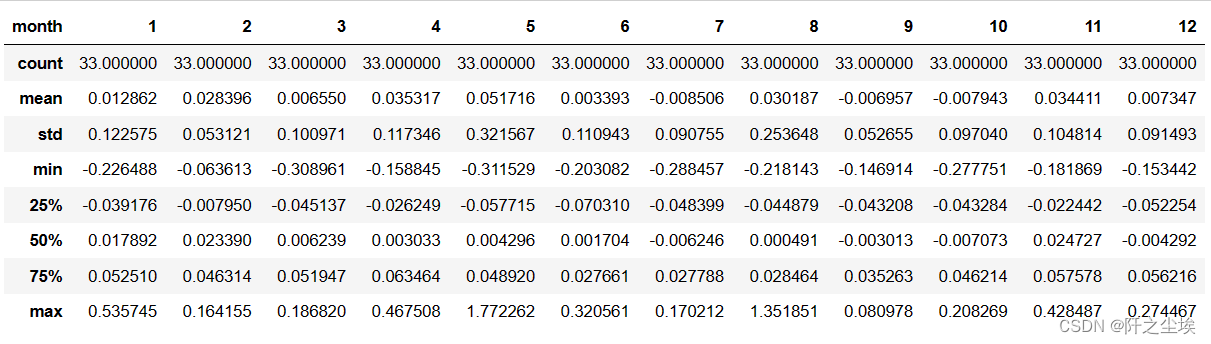
每个月的收益率和均值方差,一目了然。
简单做个t检验,来看看哪几个月的收益率存在显著性差异
import scipy.stats as stats
for i in range(len(data.columns)):for j in range(i + 1, len(data.columns)):t_statistic, p_value = stats.ttest_ind(data[data.columns[i]], data[data.columns[j]])if p_value < 0.05:print(f"0.05的显著性水平下,{data.columns[i]}月和{data.columns[j]}月有显著性差异")

画出每个月的箱线图:
#查看特征变量的箱线图分布
columns = data.columns.tolist() # 列表头
dis_cols = 4 #一行几个
dis_rows = len(columns)
plt.figure(figsize=(4 * dis_cols, 4 * dis_rows))for i in range(len(columns)):plt.subplot(dis_rows,dis_cols,i+1)sns.boxplot(data=data[columns[i]].to_numpy(), orient="v",width=0.5)plt.xlabel(columns[i],fontsize = 20)
plt.tight_layout()
plt.show()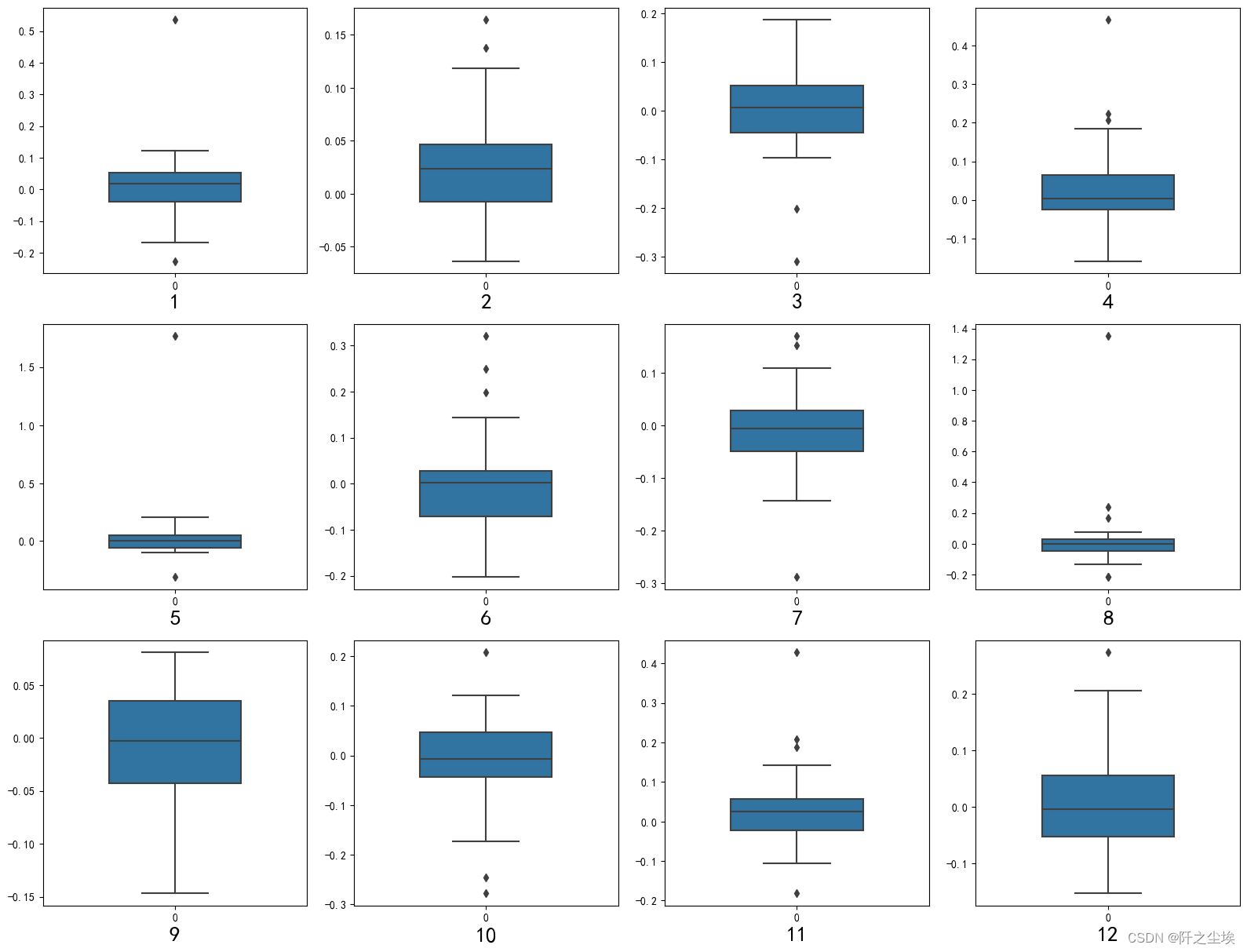
这样看不直观,数据变一下画小提琴图:
df['month']=df.index.month
df1=df[['month','monthly_return']]画图
fig = plt.figure(figsize=(14, 6), dpi=256) # 指定绘图对象宽度和高度
ax = sns.violinplot(x='month',y='monthly_return',width=0.8,saturation=0.9,lw=0.8,palette="Set2",orient="v",inner="box",data=df1)
#plt.xlabel((['月份' + str(i+1) for i in range(13)]),fontsize=10)
plt.ylabel('monthly_return', fontsize=16)
plt.show()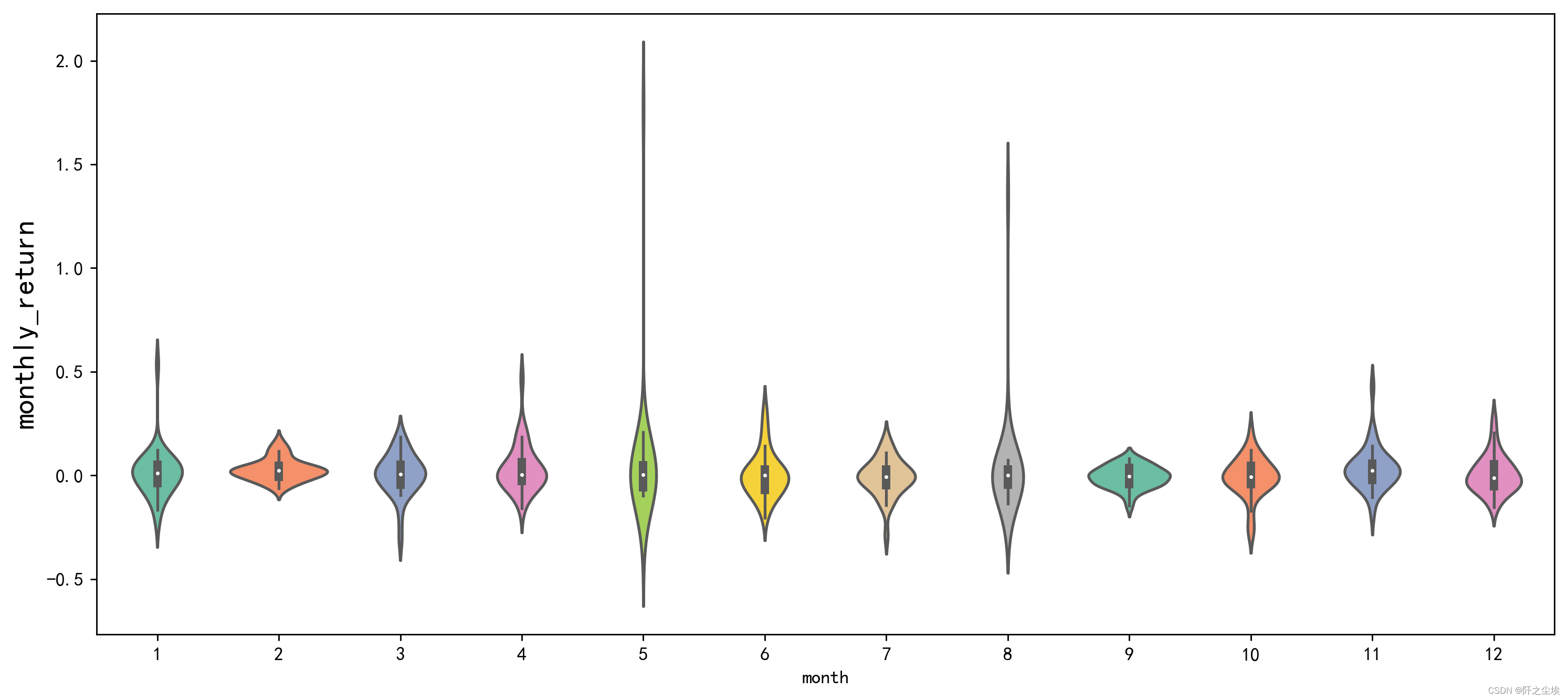
可以看到基本上每个月的收益率均值都是0附近,5月和8月的方差较大,这和历史上的某些“股灾”“金融风暴”有关。
方差分析
我们要研究的是不同月份之间的股市收益率差异,就是分类型自变量是否对数值型因变量有显著性影响,那么就是方差分析的范围了。
原假设:不同月份之间的股市收益率相同。
备择假设:不同月份之间的股市收益率存在显著性不同。
先导入包:
import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.stats.multicomp import pairwise_tukeyhsd进行方差分析:
df1['month']= df1['month'].astype('category')
model = ols('monthly_return ~ month', data=df1).fit()
anova_results = sm.stats.anova_lm(model, typ=1)
anova_results 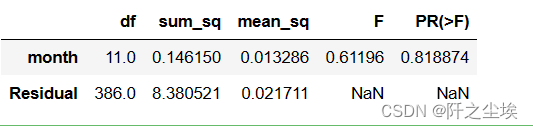
我们可以看到F值只有0.61,p值为0.8,远远不显著,说明每个月的收益率没有显著性差异。
接受原假设,即不能说明每个月的收益有显著性差异。
得到这个结果我是很惊讶的,因为我本科做的是显著的呀,奇怪,从2019年到2023年就变得不显著了???
我不死心,用虚拟变量回归的方法再试了一次。
虚拟变量回归
虚拟变量就是0和1这种哑变量,计算机里面又叫独立热编码,如果我们想表示12个月份,那么就生成一个12维的X,表示1月就第一个x为1,其他为0,表示2月就第二个x为1,其他为0.....以此类推。然后用这些X去和收益率y进行回归。
注意,在实际操作中只能生成k-1个变量,不然会陷入“虚拟变量陷阱”,即形成完美的多重共线性。
所以我删除了一月,用一月作为基准月份:
# 创建月份虚拟变量
df1 = pd.get_dummies(df1, columns=['month'], prefix='month', drop_first=True)# 构建线性回归模型,一月作为基准月份被省略
formula = 'monthly_return ~ ' + ' + '.join([col for col in df1.columns if col.startswith('month_')])
model = ols(formula, data=df1).fit()# 输出模型结果
model_summary = model.summary()
model_summary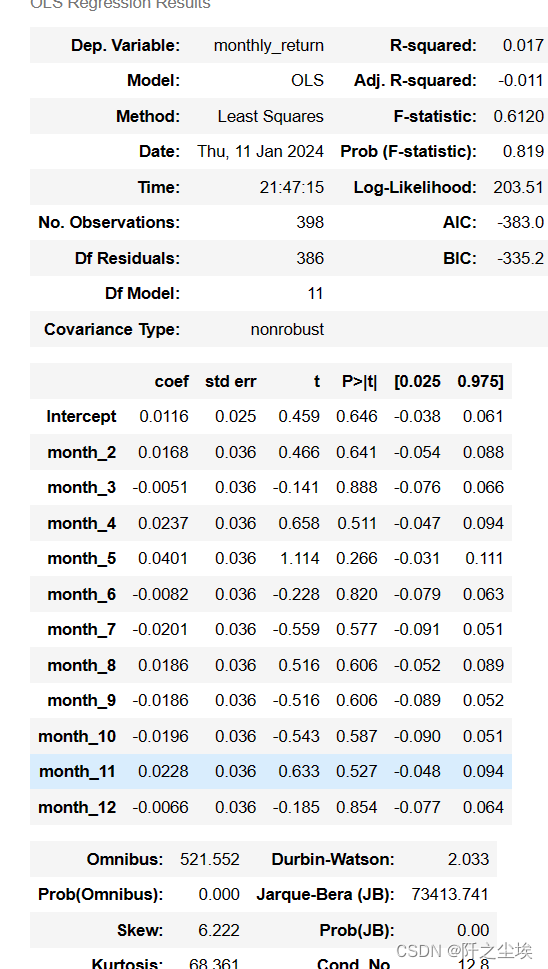
只看F值,好吧还是不显著,F值对应的p有0.8,远远不显著 。再看每个虚拟变量的t值,也没有一个显著。。。丫的,我不甘心,但是这就是现实。。我也没办法变得显著了。
之后我还尝试使用沪深300指数,我发现也是不显著。这说明,不同月份之间的A股收益率确实不存在显著性差异,那些幻想说2月份春节收益率高的,不存在....可能是某写个别的年份2月收益率高(例如2019),但是整体来看,A股30多年,不存在那些月份会有离谱的收益率。。。
虽然不显著,但是这个研究还是有意义的,起码说明了A股股市在月份效应上真的没啥规律。
当然,这案例换一下数据,换一个效应都还是很好模仿的。例如可以用个股的数据,或者某个行业的数据,研究节假日效应,季节效应,等等,都是虚拟变量,都是方差分析可以做的。
创作不易,看官觉得写得还不错的话点个关注和赞吧,本人会持续更新python数据分析领域的代码文章~(需要定制代码可私信)

)
)
)

)













)