当前版本:
- Python 3.8.4
文章目录如下
1. 介绍元组
2. 定义元组
3. 访问元组
4. 查询元组
1. 介绍元组
元组(Tuple)是一个有序的、不可变的数据序列。它可以包含各种类型的数据,例如数字、字符串、列表等。元组使用圆括号()来表示,其中的各个元素之间用逗号分隔。
与列表(List)不同,元组是不可变的,也就是说,一旦创建后,就不能修改其元素的值。这意味着不能向元组中添加、删除或修改元素。这种属性使得元组在某些情况下更加安全和可靠,例如作为字典的键值。
元组包含如下优点:
不可变性:元组的元素不可修改,这种特性使得元组在需要保护数据不被意外修改的场景下非常有用。例如,使用元组来表示一些常量或配置信息,确保它们不会被修改。
可用作字典的键:由于元组的不可变性,它们可以作为字典的键。而列表等可变对象则不能作为字典的键,因为字典的键需要是可哈希的。
性能优化:相对于列表,元组在内存占用和迭代速度方面具有优势。元组的大小和结构在创建后不会改变,这使得在创建和访问元组时更加高效。
作为函数返回值:元组常用于函数返回多个值的情况。函数可以返回一个元组,然后通过解包操作将元组的值分配给多个变量。
2. 定义元组
元组可以直接通过圆括号或 tuple 来定义。
T = () # 定义一个空元组
T = tuple() # 定义一个空元组
注意:当定义的元组只有一个元素时,需要加一个逗号。
T = ("AAA", )如果不加逗号会被识别为字符串

元组中的对象可以是数字、字符串、列表、元组、字典、集合等。
# 元组中可以包含数字、字符串、列表、元组、字典、集合等
T = (1, 2.1, 'AAA', [20], (30,), {'age':20}, {3,4})
定义元组后,里面的值是不可变的
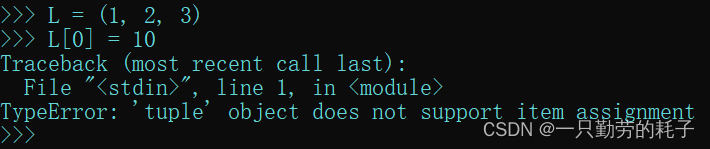
要么只能重新赋值

或者单独使用一个元组拼接其他元组
T1 = (1, 2)
T2 = ("A", "B")
T3 = T1 + T2 + ("C", "D") 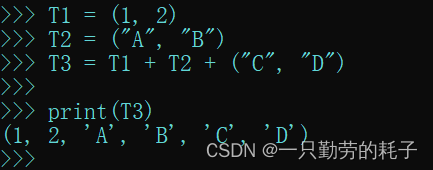

如果实在需要修改元组中的元素,那么可以先将元组转换为列表后更改,再将其转换回元组
# 定义一个元组
L = ("A", "B", 1, 2, 3)# 将元组转换为列表后,修改第2个元素
L = list(L)
L[1] = "EEE"# 再将该列表转换回元组
L = tuple(L)
3. 访问元组
- 访问元组最多的方式是通过索引取出单个元素或多个元素,或者使用遍历的方式将其全部取出,逐个处理。
1、通过索引来访问元组,索引的值从0开始,每个索引值对应一个元素。第1个元素的索引为0,第2个元素的索引为1,以此类推。。。
元组元素: A B C D E
正序索引: 0 1 2 3 4
反向索引:-5 -4 -3 -2 -1【案例一】访问单个元素
- 变量[索引] :在需要访问的变量后面加方括号,在方括号中指定索引值即可。
T = ("A", "B", "C", "D", "E")
T[0] # 访问第1个元素
T[2] # 访问第3个元素
T[-1] # 访问最后一个元素
【案例二】使用切片访问多个元素
- 变量[起始索引 : 结束索引] :指定一个开始索引值和结束索引值(范围性访问),最多只访问结束索引的前一个。
T = ("A", "B", "C", "D", "E")
T[1:3] # 访问索引为1、2的值
T[:2] # 访问前2个元素
T[-2:] # 访问后2个元素
【案例三】利用步长跳过一些元素
- 变量[起始索引 : 结束索引 : 步长] :指定开始索引和结束索引后可选步长,如果不指定默认为1
T = ("A", "B", "C", "D", "E")
T[:4:2] # 访问前4个元素,步长为2
T[::3] # 访问全部元素,步长为3 
2、通过遍历元素来访问(使用for循环将元素全部遍历后进行处理)
T = (1, 2.1, 'AAA', [20], (30,), {'age':20}, {3,4})
# 遍历元组中的元素
for i in T:print(f"当前元素为:{i}")
4. 查询元组
- 这个章节主要介绍统计元素的数量,求最大值、最小值等。
1、判断元组是否包含某个元素
T = (1, 2, 3, 'AAA', 'BBB')# 判断AAA是否在元组内
'AAA' in T# 判断0是否在元组内
0 in T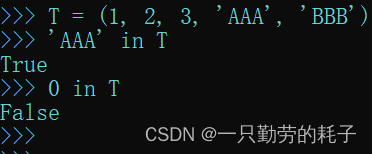
2、统计元素的个数
T = (1, 2, 3, 'AAA', 'BBB')
len(T) # 统计长度
3、统计某个元素在元组中出现的次数
T = (1, 2, 3, 'AAA', 'BBB')
T.count('AAA') # 统计某个元素出现的次数
4、求最大值(元组内仅支持数字)
L = (1, 18, 5, 20)
max(L)
5、求最小值(元组内仅支持数字)
L = (1, 18, 5, 20)
min(L)
6、求和(元组内仅支持数字)
L = (1, 18, 5, 20)
sum(L)
7、求平均值(元组内仅支持数字)
L = (1, 18, 5, 20)
avg = sum(L) / len(L)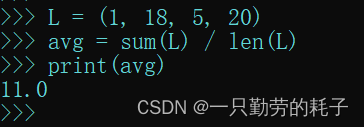

)


)

)











)
