哈希（hash）

目录

一、什么是哈希

二、哈希冲突

三、哈希函数

3.1、哈希函数设计原则

3.2、常见的哈希函数

四、哈希冲突解决

4.1、闭散列

4.2、开散列

五、哈希表的模拟实现

5.1、哈希表的功能模拟实现

5.2、测试模拟实现：

一、什么是哈希

如果构造一种存储结构，可以通过某种函数 (hashFunc) 使元素的存储位置与它的关键码之间能够建立一对一的映射关系，那么在查找时通过该函数就可以很快找到该元素；当向该结构中：

        插入元素时：根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放；
        搜索元素时：对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功。


该方法即为 哈希 (散列) 方法，哈希方法中使用的转换函数称为哈希 (散列) 函数，构造出来的结构称为哈希表 (Hash Table) (或者称散列表)。

特别注意：我们上面提到的不管是顺序搜索、平衡树搜索还是哈希搜索，其 key 值都是唯一的，也就是说，搜索树中不允许出现相同 key 值的节点，哈希表中也不允许出现相同 key 值的元素，我们下文所进行的所有操作也都是在这前提之上进行的。

二、哈希冲突

我们先来看一道题目：

现有数组{1，7，6，4，5，9}；

哈希函数设置为：hash(key) = key % capacity;    capacity为存储元素底层空间总的大小。

用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快
问题：按照上述哈希方式，向集合中插入元素44，会出现什么问题？
我们会发现，4这个位置已经有了元素占位了，所以放不进去，所以就会出现哈希冲突。
哈希冲突： 不同关键字通过相同哈希函数计算出相同的哈希地址，该种现象称为哈希冲突
或哈希碰撞。把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。

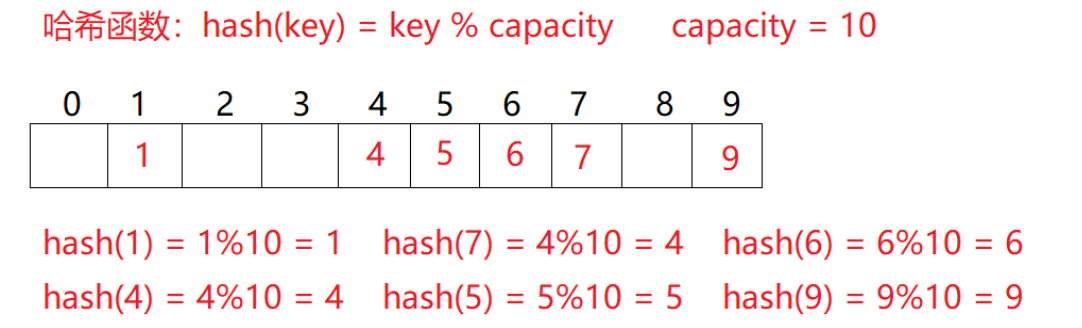
三、哈希函数

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。

3.1、哈希函数设计原则

1、哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值
域必须在0到m-1之间
2、哈希函数计算出来的地址能均匀分布在整个空间中
3、哈希函数应该比较简单

3.2、常见的哈希函数

1、 直接定址法--(常用)
取关键字的某个线性函数为散列地址： Hash（Key）= A*Key + B
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
使用场景：适合查找比较小且连续的情况

2、 除留余数法--(常用)

设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，
按照哈希函数： Hash(key) = key% p    (p<=m),将关键码转换成哈希地址
3. 平方取中法--(了解)
假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况
4、 折叠法--(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这
几部分叠加求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况
5、 随机数法--(了解)
选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中
random为随机数函数。
通常应用于关键字长度不等时采用此法
6、数学分析法--(了解)
设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定
相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只
有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散
列地址。例如：

                         

假设要存储某家公司员工登记表，如果用手机号作为关键字，那么极有可能前7位都是 相同
的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取工作还容易出现 冲突，还
可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移
位、前两数与后两数叠加(如1234改成12+34=46)等方法。
数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的
若干位分布较均匀的情况
注意：哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突

四、哈希冲突解决

解决哈希冲突两种常见的方法是：闭散列和开散列

4.1、闭散列

闭散列：也叫 开放定址法 ，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有
空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。
随之而来问题就是：我们该如果如何寻找下一个空位置呢？
线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。

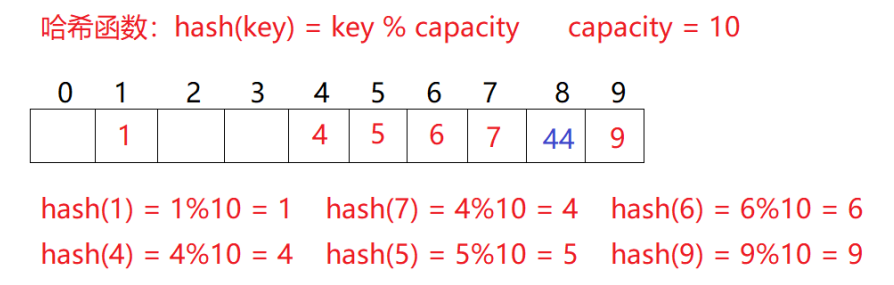
比如我们上面举的例子：现在我们需要插入44这个元素，先通过哈希函数计算哈希地址，hashAddr为4， 因此44理论上应该插在该位置，但是该位置已经放了值为4的元素，即发生哈希冲突。

插入一个元素：

1、通过哈希函数获取待插入元素在哈希表中的位置

2、如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突，使用线性探测找到下一个空位置，插入新元素。

删除一个元素：

采用闭散列处理哈希冲突时，不能随便物理删除哈希表中已有的元素，若直接删除元素 会影响其他元素的搜索。比如删除元素4，如果直接删除掉，44查找起来可能会受影 响。因此线性探测采用标记的伪删除法来删除一个元素。 
// 哈希表每个空间给个标记
// EMPTY此位置空， EXIST此位置已经有元素， DELETE元素已经删除
enum State
{EMPTY,   //空EXIST,   //有元素DELETE   //删除了 
};

线性探测的实现：

//线性探测的实现
template<class K, class V>
class HashTable
{struct Elem{pair<K, V> _val;State _state;};public:HashTable(size_t capacity = 3):_ht(capacity, _size(0)){for (size_t i = 0; i < capacity; ++i){_ht[i]._state = EMPTY;}}bool Insert(const pair<K, V>& val){size_t hashAddr = HashFunc(key);while (_ht[hashAddr] != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first == key)return false;hashAddr++;if (hashAddr == _ht.capacty())hashAddr = 0;}_ht[hashAddr]._state = EXIST;_ht[hashAddr]._val = val;_size++;return true;}int Find(const K& key){size_t hashAddr = HashFunc(key);while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val._first == key)return hashAddr;hashAddr++;}return hashAddr;}bool Erase(const K& key){int index = Find(key);if (index != -1){_ht[index]._state = DELETE;_size--;return true;}return false;}
private:size_t HashFunc(const K& key)return key % _ht.capacity();
private:vector<Elem> _ht;size_t _size;
};

现在我们海奥面对一个问题：就是哈希表什么情况下需要扩容？怎样扩容？

散列表的载荷因子定义为： \alpha= 填入表中的元素个数 / 散列表的长度

\alpha是散列表装满程度的标志因子，由于表长是定值，\alpha与“填入表中的元素个数”成正比，\alpha越大填入表中元素越多，产生冲突的可能性越大；反之，\alpha越小填入表中的元素越少，产生冲突的可能性就越小；实际上，散列表的平均查找长度是载荷因子\alpha的函数，只是不同处理冲突的方法有不同的函数；

        对于开放定址法，载荷因子是特别重要因素，应严格限制在0.7-0.8以下；超过0.8，查表时cpu缓存不命中(cache missing)按照指数曲线上升，因此一些采用开放定址法的hash库，如Java的系统库限制了载荷因子为0.75，超过此值将resize散列表；

void CheckCapacity()
{if (_size * 10 / _ht.capacity() >= 7){HashTable(K, V, HF) newHt(GetNextPrime(ht.capacity));for (size_t i = 0; i < _ht.capacity(); ++i){if (_ht[i]._state == EXIST)newHt.Insert(_ht[i]._val);}Swap(newHt);}
}

二次探测

性探测的缺陷时产生冲突的数据堆积在一块，这与其找下一个位置有关系，因为找空位置的方式就是挨个往后逐个查找的；二次探测就是为了避免该问题的，找下一个空位置的方法为，
（i=1,2,3...，是通过散列函数Hash(X)对元素的关键码key进行计算得到的位置，m表示表的大小）；

对于上面的例子 中如果要插入 44 ，产生冲突，使用解决后的情况为：44-6*6=8

        研究表明，当表长度为质数且表转载因子不超过0.5时，新表项一定能够插入，而且任何一个位置都不会被探查两次，因此只要表中有一半的位置，就不会存在表满的问题，在搜索时可以不考虑表装满的情况，但在插入时必须确保表的装载因子不超过0.5，如超过需考虑增容；

因此：比散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷。

4.2、开散列

1. 开散列概念
开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地
址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链
接起来，各链表的头结点存储在哈希表中。

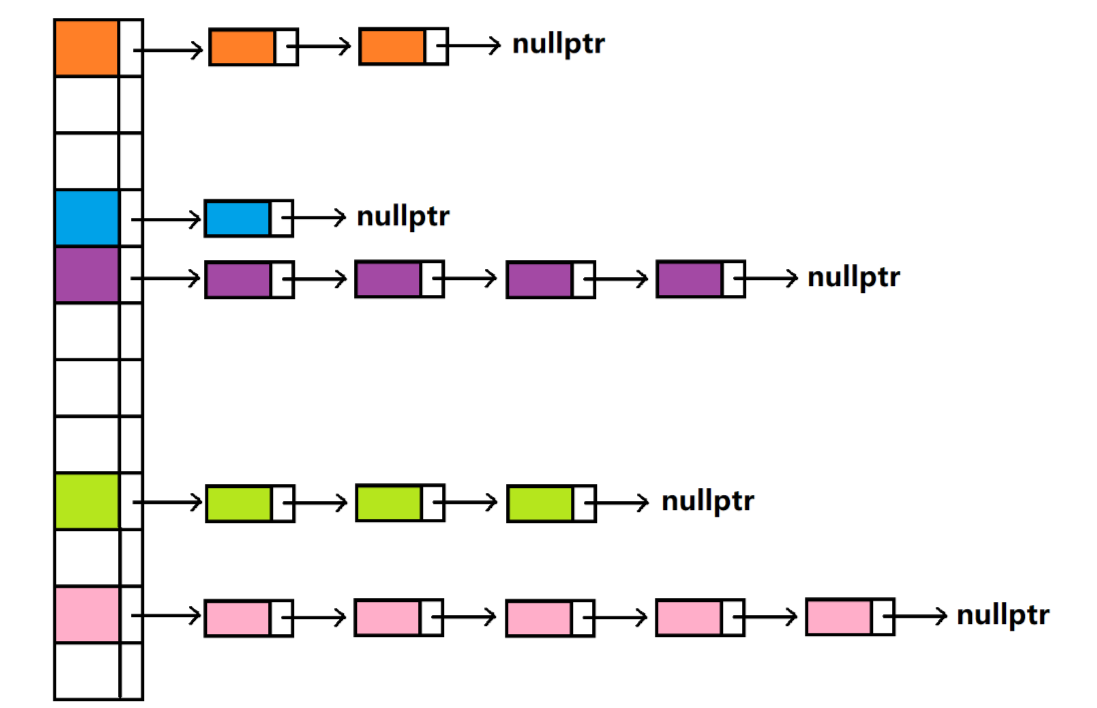
从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。

2、开散列的实现：

//开散列的实现
template<class V>
struct HashBucketNode
{HashBucketNode(const V& data):_pNext(nullptr),_data(data){}HashBucketNode<V>* _pNext;V _data;
};template<class V>
class HashBucket
{typedef HashBucketNode<V> Node;typedef Node* pNode;
public:HashBucket(size_t capacity = 3):_size(0){_ht.resize(GetNextPrime(capacity), nullptr);}pNode* Insert(const V& data){size_t bucketNo = HashFunc(data);pNode pCur = _ht[bucketNo];while (pCur){if (pCur->_data == data)return pCur;pCur = pCur->_pNext;}pCur = new Node(data);pCur->_pNext = _ht[bucketNo];_ht[bucketNo] = pCur;_size++;return pCur;}pNode* Erase(const V& data){size_t bucketNo = HashFunc(data);pNode pCur = _ht[bucketNo];pNode pPrev = nullptr;pNode pRet = nullptr;while (pCur){if (pCur->_data == data){if (pCur == _ht[bucketNo])_ht[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;pRet = pCur->_pNext;delete pCur;_size--;return pRet;}}return nullptr;}pNode* Find(const V& data);size_t Size()const;bool Empty()const;void Clear();bool BucketCount()const;void Swap(HashBucket<V, HF>& ht);~HashBucket();
private:size_t HashFunc(const V& data){return data % _ht.capacity();}
private:vector<pNode*> _ht;size_t _size;
};

3、开散列的增容

桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可
能会导致一个桶中链表节点非常多，会影响的哈希表的性能，因此在一定条件下需要对哈希
表进行增容，开散列最好的情况是：每个哈希桶中刚好挂一个节点， 再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可 以给哈希表增容。 
void _CheckCapacity()
{size_t bucketCount = BucketCount();if (_size == bucketCount){HashBucket<V, HF> newHt(bucketCount);for (size_t bucketIdx = 0; bucketIdx < bucketCount; ++bucketIdx){pNode pCur = _ht[bucketIdx];while (pCur){_ht[bucketIdx] = pCur->_pNext;size_t bucketNo = newHt.HashFunc(pCur->_data);pCur->_pNext = newHt._ht[bucketNo];newHt._ht[bucketNo] = pCur;pCur = _ht[bucketIdx];}}newHt._size = _size;this->Swap(newHt);}
}

4. 开散列的思考

1. 只能存储key为整形的元素，其他类型怎么解决？

// 哈希函数采用处理余数法，被模的key必须要为整形才可以处理，此处提供将key转化为
整形的方法
// 整形数据不需要转化
template<class T>
class DefHashF
{
public:size_t operator()(const T& val){return val;}
};
// key为字符串类型，需要将其转化为整形
class Str2Int
{
public:size_t operator()(const string& s){const char* str = s.c_str();unsigned int seed = 131; // 31 131 1313 13131 131313unsigned int hash = 0;while (*str){hash = hash * seed + (*str++);}return (hash & 0x7FFFFFFF);}
};
// 为了实现简单，此哈希表中我们将比较直接与元素绑定在一起
template<class V, class HF>
class HashBucket
{// ……
private:size_t HashFunc(const V& data){return HF()(data.first)%_ht.capacity();}
};

2. 除留余数法，最好模一个素数，如何每次快速取一个类似两倍关系的素数？

size_t GetNextPrime(size_t prime){const int PRIMECOUNT = 28;static const size_t primeList[PRIMECOUNT] ={53ul, 97ul, 193ul, 389ul, 769ul,543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul,                                             98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,1610612741ul, 3221225473ul, 4294967291ul};size_t i = 0;for (; i < PRIMECOUNT; ++i){if (primeList[i] > prime)return primeList[i];}return primeList[i];
}
5. 开散列与闭散列比较
应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上： 由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <= 0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。

五、哈希表的模拟实现

5.1、哈希表的功能模拟实现

#pragma once
#include<iostream>
#include<vector>
#include<string>using std::cin;
using std::cout;
using std::endl;
using std::vector;
using std::string;
using std::pair;
using std::make_pair;//选出key
template<class K, class V>
struct PairSelect1st
{const K& operator()(const pair<K, V>& kv) { return kv.first; }
};
template<class K>
struct KSelect1st
{const K& operator()(const K& k) { return k; }
};//转成整型
template<class K>
struct HashFunc
{size_t operator()(const K& val) { return val; }
};
//模板的特化
template<>
struct HashFunc<std::string>
{size_t operator()(const std::string& s1){size_t sum = 0;for (size_t i = 0; i < s1.size(); i++){sum = sum * 131 + s1[i];}return sum;}
};//比较判断
template<class K>
struct equal_to
{bool operator()(const K& lval, const K& rval) { return lval == rval; }
};
template<>
//模板特化
struct equal_to<std::string>
{bool operator()(const std::string& s1, const  std::string& s2) { return s1 == s2; }
};//素数表
const int PRIMECOUNT = 28;
const size_t primeList[PRIMECOUNT] = {53ul, 97ul, 193ul, 389ul, 769ul,1543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul, 98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,1610612741ul, 3221225473ul, 4294967291ul
};
namespace OpenHash
{template<class T>struct HashNode{typedef HashNode<T> Node;typedef HashNode<T>* pNode;HashNode<T>* _next;T _data;public:HashNode(const T& data = T()):_next(nullptr),_data(data){}};template<class K, class V, class T, class Pred, class Select1st ,class HashFunc>class HashTable;template<class K, class V, class T, class Ref, class Ptr, class Pred, class Select1st, class HashFunc>struct Iterator{typedef HashNode<T> Node;typedef HashTable<K, V, T, Pred, Select1st, HashFunc> HashTable;typedef Iterator<K, V, T, Ref, Ptr, Pred, Select1st, HashFunc> self;Node* _pnode;HashTable* _pHT;Iterator(Node* pnode = nullptr, HashTable* pHT = nullptr) : _pnode(pnode), _pHT(pHT) {  }Ref operator*() { return _pnode->_data; }const Ref operator*()const { return _pnode->_data; }Ptr operator->() { return &_pnode->_data; }const Ptr operator->()const { return &_pnode->_data; }self& operator++(){if (_pnode == nullptr)return *this;if (_pnode->_next != nullptr){_pnode = _pnode->_next;return *this;}//_pnode->next == nullptr我们要去找现在的结点属于哪一个桶size_t index = HashFunc()(Select1st()(_pnode->_data)) % _pHT->_table.size() + 1;for (; index < _pHT->_table.size(); index++){Node* cur = _pHT->_table[index];if (cur != nullptr){_pnode = cur;return *this;}}_pnode = nullptr;return *this;}self operator++(int){self tmp = *this;++(*this);return tmp;}bool operator!=(const self& it)const { return _pnode != it._pnode; }bool operator==(const self& it)const { return _pnode == it._pnode; }};template<class K, class V, class T, class Pred = equal_to<std::string>,class Select1st = PairSelect1st<K, V>, class HashFunc = HashFunc<K>>class HashTable{typedef HashNode<T>* pNode;typedef HashNode<T> Node;template<class K, class V, class T, class Ref, class Ptr, class Pred, class Select1st, class HashFunc>friend  struct Iterator;private://存结点指针vector<pNode> _table;size_t _n;	public:typedef Iterator<K, V, T, const T&, const T* ,Pred, Select1st, HashFunc> const_iterator;typedef Iterator<K, V, T, T&, T*, Pred, Select1st, HashFunc> iterator;HashTable() :_n(0) {  }void clear(){		for (size_t index = 0; index < _table.size(); index++){pNode cur = _table[index];pNode prev = cur;while (cur){prev = cur;cur = cur->_next;delete prev;}}}~HashTable(){clear();}iterator begin(){size_t index = 0;for (; index < _table.size(); index++){pNode cur = _table[index];if (cur != nullptr)return iterator(cur,this);}return iterator(nullptr, this);}iterator end() { return iterator(nullptr, this); }const_iterator cbegin(){size_t index = 0;for (; index < _table.size(); index++){pNode cur = _table[index];if (cur != nullptr)return const_iterator(cur, this);}return const_iterator(nullptr, this);}const_iterator cend() { return const_iterator(nullptr, this); }pair<iterator,bool> insert(const T& data){//如果为空，则开空间if (!_table.size())_table.resize(53ul);//挑选keySelect1st st1;//转换整型HashFunc hf;//判断是否冗余iterator ret = find(data);if (ret._pnode != nullptr)return std::make_pair(iterator(nullptr,this), false);//判断是否需要扩容if ((double)_n / (double)_table.size() >= 1){vector<pNode> new_table(GetNextPrime(_table.size()));for (size_t i = 0; i < _table.size(); i++){pNode cur = _table[i];if (cur != nullptr){		pNode next = _table[i];while (cur){next = cur->_next;size_t new_index = (hf(st1(cur->_data))) % new_table.size();//头插cur->_next = new_table[new_index];new_table[new_index] = cur;cur = next;}_table[i] = nullptr;}//不推荐，插入的时候重新创建结点，浪费/*while(e != nullptr){tmp.insert(e->_kv);e = e->_next;}*/}new_table.swap(_table);}		//计算hashbucket的下标size_t index = hf(st1(data)) % _table.size();pNode newNode = new  Node(data);//头插newNode->_next = _table[index];_table[index] = newNode;_n++;return std::make_pair(iterator(newNode,this), true);}iterator find(const T& data){HashFunc hf;Select1st slt;if (_table.size() == 0)return iterator(nullptr,this);size_t index = hf(slt(data)) % _table.size();pNode cur = _table[index];while (cur){if (Pred()(slt(cur->_data), slt(data)))return iterator(cur,this);					elsecur = cur->_next;}return iterator(nullptr,this);}bool erase(const T& data){		Select1st st1;size_t index = HashFunc()(st1(data)) % _table.size();pNode cur = _table[index];pNode prev = cur;while (cur){if (Pred()(st1(cur->_data) , st1(data))){//找到了if (cur == _table[index]){_table[index] = cur->_next;_n--;delete cur;return true;}else{prev->_next = cur->_next;_n--;delete cur;return true;}}else//没找到{prev = cur;cur = cur->_next;}}return false;}size_t GetNextPrime(size_t prime){size_t i = 0;for (; i < PRIMECOUNT; i++){if (primeList[i] > prime)return primeList[i];}return primeList[i];}size_t size() const{ return _n; }};
}

5.2、测试模拟实现：

//OpenHash(开散列)
void Test_KV2()//KV模型
{OpenHash::HashTable<string, string, pair<string, string>> hts;pair<string, string> arr[] = { make_pair("left", "左边") ,make_pair("right", "右边"),make_pair("up", "向上"),make_pair("down", "向下"),make_pair("left","左边"),make_pair("eat","吃"),make_pair("sleep","睡觉"),make_pair("run","跑"),make_pair("jump","跳")};for (auto e : arr)hts.insert(e);//非const迭代器OpenHash::HashTable<string, string, pair<string, string>>::iterator it = hts.begin();while (it != hts.end()){cout << it->first << ":" << it->second << endl;it++;}cout << endl;hts.erase(make_pair("sleep", "睡觉"));hts.erase(make_pair("left", "左边"));hts.erase(make_pair("up", "向上"));//const类型OpenHash::HashTable<string, string, pair<string, string>>::const_iterator cit = hts.cbegin();while (cit != hts.cend()){cout << cit->first << ":" << cit->second << endl;cit++;}cout << endl;
}void Test_K2()//K模型
{OpenHash::HashTable<string, string, string, equal_to<string>, KSelect1st<string>, HashFunc<string>> hts;string arr[] = {"left", "左边" ,"right", "右边","up", "向上","down", "向下","left","左边","eat","吃","sleep","睡觉","run","跑","jump","跳" };for (auto e : arr)hts.insert(e);OpenHash::HashTable<string, string, string, equal_to<string>, KSelect1st<string>, HashFunc<string>>::iterator it = hts.begin();while (it != hts.end()){cout << *it << " ";it++;}cout << endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/625466.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

实例分割模型Mask2Former解析

实例分割模型Mask2Former解析

Masked2Former是在mask rcnn基础上改进的一个实例分割模型&#xff0c;参考了一些经典模型的思想&#xff0c;如DETR&#xff0c;实验表明效果很好。 论文&#xff1a;《Masked-attention Mask Transformer for Universal Image Segmentation》 https://arxiv.org/abs/2112.0…
阅读更多...
新手必看：腾讯云服务器购买详细图文教程

新手必看：腾讯云服务器购买详细图文教程

腾讯云服务器购买流程很简单&#xff0c;有两种购买方式&#xff0c;直接在官方活动上购买比较划算&#xff0c;在云服务器CVM或轻量应用服务器页面自定义购买价格比较贵&#xff0c;但是自定义购买云服务器CPU内存带宽配置选择范围广&#xff0c;活动上购买只能选择固定的活动…
阅读更多...
【极光系列】Windows安装Mysql8.0版本

【极光系列】Windows安装Mysql8.0版本

【极光系列】Windows安装Mysql8.0版本 一.mysql服务端 下载地址&#xff1a;https://dev.mysql.com/downloads/mysql/ 二.解压二进制包 解压到 E:\mysql-8.0.35-winx64目录下&#xff0c;记住你解压后的目录&#xff0c;后续要使用三.创建my.ini文件 tips&#xff1a;mys…
阅读更多...
nvcc -V显示command not found

nvcc -V显示command not found

出现这个问题&#xff0c;不仅是 nvcc -V会显示command not found,nvidia-smi同样也会显示 解决方法如下&#xff1a; 1&#xff09;这里首先转换到CUDA所在位置&#xff0c;一般是在这个位置 cd /usr/local 2&#xff09;打开、编辑环境变量的配置文件 vim ~/.bashrc …
阅读更多...
使用HTTP/2在Linux上的Nginx服务器进行优化

使用HTTP/2在Linux上的Nginx服务器进行优化

随着互联网的发展&#xff0c;HTTP/2协议逐渐成为主流。与传统的HTTP/1.1相比&#xff0c;HTTP/2提供了更高的传输效率和更好的安全性。在Linux上使用Nginx服务器进行优化&#xff0c;我们可以充分利用HTTP/2的优势&#xff0c;提高网站的性能和用户体验。 1. 安装Nginx并启用…
阅读更多...
日志采集传输框架之 Flume，将监听端口数据发送至Kafka

日志采集传输框架之 Flume，将监听端口数据发送至Kafka

1、简介 Flume 是 Cloudera 提供的一个高可用的&#xff0c;高可靠的&#xff0c;分布式的海量日志采集、聚合和传 输的系统。Flume 基于流式架构&#xff0c;主要有以下几个部分组成。 主要组件介绍&#xff1a; 1&#xff09;、Flume Agent 是一个 JVM 进程&#xf…
阅读更多...
【JupyterLab】在 conda 虚拟环境中 JupyterLab 的安装与使用

【JupyterLab】在 conda 虚拟环境中 JupyterLab 的安装与使用

【JupyterLab】在 conda 虚拟环境中 JupyterLab 的安装与使用 1 JupyterLab 介绍2 安装2.1 Jupyter Kernel 与 conda 虚拟环境 3 使用3.1 安装中文语言包(Optional)3.2 启动3.3 常用快捷键3.3.1 命令模式下 3.4 远程访问个人计算机3.4.1 局域网下 1 JupyterLab 介绍 官方文档: …
阅读更多...
15.鸿蒙HarmonyOS App(JAVA)进度条与圆形进度条

15.鸿蒙HarmonyOS App(JAVA)进度条与圆形进度条

15.鸿蒙HarmonyOS App(JAVA)进度条与圆形进度条 progressBar2.setIndeterminate(true);//设置无限模式,运行查看动态效果 //创建并设置无限模式元素 ShapeElement element new ShapeElement(); element.setBounds(0,0,50,50); element.setRgbColor(new RgbColor(255,0,0)); …
阅读更多...
Nginx——强化基础配置

Nginx——强化基础配置

1、牢记Context Context是Nginx中每条指令都会附带的信息&#xff0c;用来说明指令在哪个指令块中使用&#xff0c;可以将Context 理解为配置环境。 每个指令都拥有自己的配置环境&#xff0c;如果把配置环境记错了&#xff0c;或者在设计时未考虑配置环境的作用&#xff0c;…
阅读更多...
【闯关练习】—— 1400分（构造）

【闯关练习】—— 1400分（构造）

&#x1f30f;博客主页&#xff1a;PH_modest的博客主页 &#x1f6a9;当前专栏&#xff1a;cf闯关练习 &#x1f48c;其他专栏&#xff1a; &#x1f534;每日一题 &#x1f7e1; C跬步积累 &#x1f7e2; C语言跬步积累 &#x1f308;座右铭&#xff1a;广积粮&#xff0c;缓…
阅读更多...
STM32F103标准外设库——寄存器 (二)

STM32F103标准外设库——寄存器 (二)

个人名片&#xff1a; &#x1f981;作者简介&#xff1a;一名喜欢分享和记录学习的在校大学生 &#x1f42f;个人主页&#xff1a;妄北y &#x1f427;个人QQ&#xff1a;2061314755 &#x1f43b;个人邮箱&#xff1a;2061314755qq.com &#x1f989;个人WeChat&#xff1a;V…
阅读更多...
LeetCode刷题---逆波兰表达式求值

LeetCode刷题---逆波兰表达式求值

解题思路&#xff1a; 使用栈来解决该问题 首先定义一个栈Stack&#xff0c;接着对tokens数组进行遍历&#xff0c;如果当前元素是非数字字符串的话(运算符)&#xff0c;就从栈中取出两个元素根据该运算符进行计算&#xff0c;将计算后的结果添加到栈中。如果当前元素是数字字符…
阅读更多...
基于Spring Boot+vue的云上新鲜水果超市商城系统

基于Spring Boot+vue的云上新鲜水果超市商城系统

本云上水果超市是为了提高用户查阅信息的效率和管理人员管理信息的工作效率&#xff0c;可以快速存储大量数据&#xff0c;还有信息检索功能&#xff0c;这大大的满足了用户、员工信息和管理员这三者的需求。操作简单易懂&#xff0c;合理分析各个模块的功能&#xff0c;尽可能…
阅读更多...
【翻译】Qt Designer 如何使用资源文件

【翻译】Qt Designer 如何使用资源文件

原文地址&#xff1a;https://doc.qt.io/qt-6/designer-resources.html Qt的资源浏览器是用于管理应用程序资源的工具&#xff0c;可以让开发者方便地查看和管理应用程序中的各种资源文件&#xff0c;例如图像、字体、布局文件、对话框等。 资源浏览器提供了一个可视化的界面&…
阅读更多...
【Golang】二进制字符串转换为数字

【Golang】二进制字符串转换为数字

在本文中&#xff0c;我们将探讨如何使用 Go 语言将十六进制字符串转换为二进制字符串&#xff0c;将不定长整型补码字符串转换为数字&#xff0c;以及如何将 IEEE754 标准的单精度&#xff08;32位&#xff09;和双精度&#xff08;64位&#xff09;浮点数字符串转换为数字。最…
阅读更多...
商业世界，从2023到2024

商业世界，从2023到2024

作者&#xff5c;潮汐商业评论 编辑&#xff5c;Ray 变化总在发生&#xff0c;你不去迎接进步的变化&#xff0c;就会等到退步的变化。 —— 查理.芒格 2023, 我们似乎总在不断告别。从“一生自由”的大家黄永玉到“智慧”投资家查理.芒格&#xff0c;再到写出《不能承受的生命…
阅读更多...
Zung氏抑郁自评量表SDS

Zung氏抑郁自评量表SDS

抑郁症是常见的心理障碍&#xff0c;其症状表现为&#xff1a;心境低落、思维迟缓、意志活动减退、认知功能损害、躯体症状等。在生活中常有悲观消沉&#xff0c;灰心丧气&#xff0c;对所有事情都提不起兴趣&#xff0c;严重的还会出现肢体僵硬和耳鸣等症状。 部分人有明显的…
阅读更多...
10分钟快速上手LLM大模型Python前端开发（三）之显示模块（一）

10分钟快速上手LLM大模型Python前端开发（三）之显示模块（一）

10分钟快速上手LLM大模型Python前端开发&#xff08;三&#xff09;之显示模块&#xff08;一&#xff09; 显示代码初步测试 通用显示方法显示字符串显示dataframe显示Markdown 微信公众号&#xff1a;leetcode_algos_life&#xff0c;代码随想随记 小红书&#xff1a;4124081…
阅读更多...
Linux网络文件共享服务

Linux网络文件共享服务

目录 一.文件存储类型 1.直连式存储&#xff1a;Direct-Attached Storage&#xff0c;简称DAS 2.存储区域网络&#xff1a;Storage Area Network&#xff0c;简称SAN&#xff08;可以使用空间&#xff0c;管理也是你来管理&#xff09; 3.网络附加存储&#xff1a;Network-…
阅读更多...
运筹说 第67期 | 动态规划模型的建立与求解

运筹说 第67期 | 动态规划模型的建立与求解

通过前一期的学习&#xff0c;我们已经学会了动态规划的基本概念和基本原理。本期小编带大家学习动态规划模型的建立与求解。 动态规划模型的建立 一 概述 建立动态规划的模型&#xff0c;就是分析问题并建立问题的动态规划基本方程。 成功地应用动态规划方法的关键&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023