在本文中,我们将探讨如何使用 Go 语言将十六进制字符串转换为二进制字符串,将不定长整型补码字符串转换为数字,以及如何将 IEEE754 标准的单精度(32位)和双精度(64位)浮点数字符串转换为数字。最后,我们将讨论如何将布尔类型的二进制字符串转换为布尔值。
- 十六进制字符串转二进制字符串
- 不定长整型补码字符串转数字
- IEEE754 标准浮点数字符串转数字
- 单精度浮点数
- 双精度浮点数
- 布尔类型字符串转布尔类型
- 测试
- 测试结果
十六进制字符串转二进制字符串
package compute
import ("errors""strconv""strings"
)
// HexToBinary 将十六进制字符串转换为二进制字符串。
func HexToBinary(hex string) (string, error) {decimal, err := strconv.ParseInt(hex, 16, 64)if err != nil {return "", err}// 使用 strconv.FormatInt 把整数转换为二进制字符串。binaryStr := strconv.FormatInt(decimal, 2)// 计算需要补充的0的个数。diff := len(hex)*4 - len(binaryStr) // 补全至正确的长度。return strings.Repeat("0", diff) + binaryStr, nil
}
这段代码首先定义了一个函数 HexToBinary,它接受一个十六进制字符串,并返回相应的二进制字符串。它使用 strconv.ParseInt 函数将十六进制字符串转换为整数,然后用 strconv.FormatInt 转换为二进制字符串。如果输入的字符串不能正确转换,函数将返回一个错误。<链接>
不定长整型补码字符串转数字
package compute
import ("errors""math""strconv"
)
// BinaryIntegerStringToInt 将不定长整型补码字符串转换为数字。
func BinaryIntegerStringToInt(binaryStr string) (num int64, err error) {// 解析二进制补码字符串为整数。num, err = strconv.ParseInt(binaryStr, 2, 64)if err != nil {return}// 如果最高位是1,则表示这是一个负数,需要进行补码转换。if binaryStr[:1] == "1" {num -= int64(math.Pow(2, float64(len(binaryStr))))}return
}
这个函数 BinaryIntegerStringToInt 用于将不定长的二进制补码字符串转换为整数。如果最高位是1,则表示这是一个负数,需要从结果中减去 2^len(binaryStr) 以得到实际的数值。<链接>
IEEE754 标准浮点数字符串转数字
单精度浮点数
package compute
import ("errors""math""strconv"
)
// BinaryFloatStringToFloat 将IEEE754标准单精度浮点数字符串转为数字。
func BinaryFloatStringToFloat(binaryStr string) (float64, error) {// 确保字符串长度为32位。n := 32 - len(binaryStr)if n >= 0 && n < 32 {binaryStr = strings.Repeat("0", n) + binaryStr} else {return 0, errors.New("unsupported binary length")}// 解析符号位。sign := 1.0if binaryStr[0] == '1' {sign = -1.0}// 解析指数位。exponent, _ := strconv.ParseInt(binaryStr[1:9], 2, 64)exponent -= 127// 解析尾数位。mantissa := float64(0)for i := 9; i < len(binaryStr); i++ {if binaryStr[i] == '1' {mantissa += 1 / (math.Pow(2, float64(i-8)))}}// 计算浮点数值。result := sign * (1 + mantissa) * (math.Pow(2, float64(exponent)))return result, nil
}
这段代码定义了一个函数 BinaryFloatStringToFloat,它将单精度浮点数的二进制字符串转换为 float64 类型的数字。它首先检查字符串的长度是否为32位,如果不是,则补足至32位。然后,它解析符号位、指数位和尾数位,并计算出最终的浮点数值。<链接>
双精度浮点数
package compute
import ("errors""math""strconv"
)
// BinaryDoubleStringToFloat 将IEEE754标准双精度浮点数字符串转为数字。
func BinaryDoubleStringToFloat(binaryStr string) (float64, error) {// 确保字符串长度为64位。n := 64 - len(binaryStr)if n >= 0 && n < 64 {binaryStr = strings.Repeat("0", n) + binaryStr} else {return 0, errors.New("unsupported binary length")}// 解析符号位。sign := 1.0if binaryStr[0] == '1' {sign = -1.0}// 解析指数位。exponent, _ := strconv.ParseInt(binaryStr[1:12], 2, 64)exponent -= 1023// 解析尾数位。mantissa := float64(0)for i := 12; i < len(binaryStr); i++ {if binaryStr[i] == '1' {mantissa += 1 / float64(math.Pow(2, float64(i-11)))}}// 计算浮点数值。result := sign * (1 + mantissa) * math.Pow(2, float64(exponent))return result, nil
}
这段代码定义了一个函数 BinaryDoubleStringToFloat,它将双精度浮点数的二进制字符串转换为 float64 类型的数字。它的处理过程与单精度浮点数的转换类似,只是字符串的长度要求是64位,并且指数位的偏移量不同。<链接>
布尔类型字符串转布尔类型
package compute
import "strings"
// BinaryBooleanStringToBoolean 将布尔类型的二进制字符串转换为布尔值。
func BinaryBooleanStringToBoolean(binaryStr string) bool {return binaryStr == "1"
}
这个函数 BinaryBooleanStringToBoolean 接受一个二进制字符串,并返回对应的布尔值。如果字符串为 “1”,则返回 true;如果为其他任何字符,则返回 false。
测试
func main() {hexString := "0f6561f02f1505"binaryString, _ := HexToBinary(hexString)fmt.Printf("十六进制字符串:%s\n二进制字符串:%s\n\n", hexString, binaryString)binaryString = "10110100101"resultInt, _ := BinaryIntegerStringToInt(binaryString)fmt.Printf("二进制字符串:%s\n转换结果:%d\n\n", binaryString, resultInt)binaryString = "11000001010010000000000000000000"result, _ := BinaryFloatStringToFloat(binaryString)fmt.Printf("二进制字符串:%s\n转换结果:%.2f\n\n", binaryString, result)binaryString = "0100000000101001100100011010000000000000000000000000000000000000"result, _ = BinaryDoubleStringToFloat(binaryString)fmt.Printf("二进制字符串:%s\n转换结果:%.5f\n\n", binaryString, result)fmt.Printf("二进制字符串:%s\n转换结果:%t\n\n", "0", BinaryBooleanStringToBoolean("0"))
}测试结果
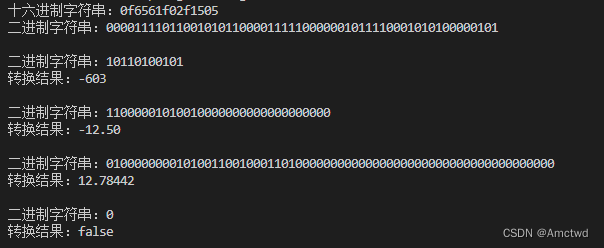
以上函数展示了如何使用 Go 语言进行不同类型数字和布尔值的转换。在实际应用中,这些函数可以作为处理二进制数据的工具,例如在解析网络数据包、处理计算机架构相关的数据或者在算法中需要进行数值计算时。确保在实际使用这些函数时,输入参数符合预期,以避免可能的运行时错误。





之显示模块(一))



)
JMeter接口压测使用(保姆式手把手教会))


:多目标粒子群优化算法(MOPSO)求解ZDT1、ZDT2、ZDT3、ZDT4、ZDT6(提供Python代码))


AC(Aho Corasick)算法的源代码)


