欢迎来到Cefler的博客😁
🕌博客主页：那个传说中的man的主页
🏠个人专栏：题目解析
🌎推荐文章：【LeetCode】winter vacation training

---

前言
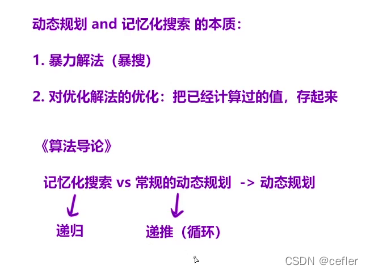
记忆化搜索是一种优化搜索算法的方法，它可以有效地减少重复计算和提高算法效率。该算法通过使用一个缓存数据结构来存储之前计算过的结果，避免了重复计算相同的问题，从而提高了搜索效率。

具体来说，记忆化搜索通常使用递归算法实现。在每次递归调用时，检查缓存中是否已经存储了当前问题的解。如果是，则直接返回缓存中的结果；否则，计算当前问题的解，并将其存储到缓存中，然后返回结果。

---

👉🏻斐波那契数

原题链接：斐波那契数

mycode:

class Solution {
public:int memory[101];//备忘录int dfs(int n){if(memory[n]!=-1){return memory[n];}if(n<2){memory[n] = n;return n;}else{memory[n] = fib(n-1)+fib(n-2);return memory[n];}}int fib(int n) {memset(memory,-1,sizeof(memory));return dfs(n);}};

记忆化搜索与常规动态规划

👉🏻不同路径

原题链接：不同路径

mycode:

class Solution {
public:int memo[101][101];//备忘录int dfs(int m,int n){if(memo[m][n]!=0){return memo[m][n];}if(m==0||n==0) return 0;if(m==1&&n==1){memo[m][n] = 1;return memo[m][n];}else{memo[m][n] = dfs(m-1,n)+dfs(m,n-1);return memo[m][n];}}int uniquePaths(int m, int n) {memset(memo,0,sizeof(memo));return dfs(m,n);}
};

👉🏻最长递增子序列

原题链接：最长递增子序列

递归暴搜（超出时间限制）

mycode:

class Solution {
public:int dfs(vector<int>& nums,int pos){int ret = 1;for(int i = pos+1;i<nums.size();i++){if(nums[i]>nums[pos]){ret = max(dfs(nums,i)+1,ret);}}return ret;}int lengthOfLIS(vector<int>& nums) {int ret = 0;for(int i = 0;i<nums.size();i++){ret = max(ret,dfs(nums,i));}return ret;}
};

记忆化搜索优化递归时间

class Solution {
public:int dfs(vector<int>& nums,int pos,vector<int>& memo){if(memo[pos]!=0) return memo[pos];int ret = 1;for(int i = pos+1;i<nums.size();i++){if(nums[i]>nums[pos]){ret = max(dfs(nums,i,memo)+1,ret);}}memo[pos] = ret;return ret;}int lengthOfLIS(vector<int>& nums) {int ret = 0;vector<int> memo(nums.size());//备忘录for(int i = 0;i<nums.size();i++){ret = max(ret,dfs(nums,i,memo));}return ret;}