报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上交流答疑:
文章目录
- 1. BFS简介和基本代码
- 2. BFS与最短路径
- 2.1 计算最短路的长度
- 2.2 输出完整的最短路径
- 3. BFS与判重
- 3.1 C++判重
- 3.2 Java判重
- 3.3 Python判重
第14周: BFS
1. BFS简介和基本代码
第12周博客用“一群老鼠走迷宫”做比喻介绍了BFS的原理,类似的比喻还有“多米诺骨牌”、“野火蔓延”。BFS的搜索过程是由近及远的,从最近的开始,一层层到达最远处。以下面的二叉树为例,一层一层地访问,从A出发,下一步访问B、C,再下一步访问D、E、F、G,最后访问H、I。圆圈旁边的数字是访问顺序。
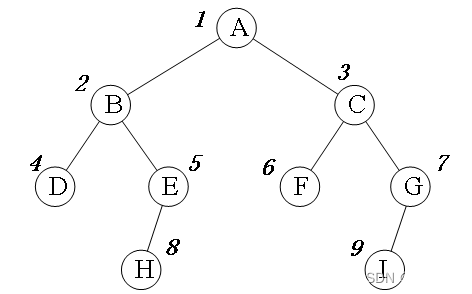
一句话概况BFS的思想:全面扩散、逐层递进。
BFS的逐层访问过程如何编程实现?非常简单,用队列,“BFS = 队列”。队列的特征是先进先出,并且不能插队。BFS用队列实现:第一层先进队列,然后第二层进队列、第三层、…。
上面图示的二叉树用队列进行BFS操作:根节点A第1个进队列;然后让A的子节点B、C进队列;接下来让B、C的子节点D、E、F、G进队列;最后让E、G的子节点H、I进队列。节点进入队列的先后顺序是A-BC-DEFG-HI,正好按层次分开了。
在任何时刻,队列中只有相邻两层的点。
下面的代码输出图示二叉树的BFS序,用队列实现。队列和二叉树参考第6周队列和第7周二叉树的讲解。
C++代码
#include <bits/stdc++.h>
using namespace std;
const int N=100;
char t[N]; //简单地用一个数组定义二叉树
int ls(int p){return p<<1;} //定位左孩子,也可以写成 p*2
int rs(int p){return p<<1 | 1;} //定位右孩子,也可以写成 p*2+1
void bfs(int root) {queue<int> q; //定义队列q.push(root); //第一个节点进入队列while (!q.empty()) { //用BFS访问二叉树int u = q.front(); //读队头,并输出cout << t[u];q.pop(); //队头处理完了,弹走if (t[ls(u)]) q.push(ls(u)); //左儿子进队列if (t[rs(u)]) q.push(rs(u)); //右儿子进队列}
}
int main(){t[1]='A'; //第1层t[2]='B'; t[3]='C'; //第2层t[4]='D'; t[5]='E'; t[6]='F'; t[7]='G'; //第3层t[10]='H'; t[14]='I'; //第4层bfs(1); //BFS访问二叉树,从根节点1开始。输出:ABCDEFGHIcout<<"\n";bfs(3); //BFS访问二叉树的子树,从子节点3开始。输出:CFGIreturn 0;
}
Java代码
import java.util.*;
public class Main {private static final int N = 100;private static char[] t = new char[N]; //简单地用一个数组定义二叉树private static int ls(int p) {return p<<1;} //定位左孩子,也可以写成 p*2private static int rs(int p) {return (p<<1) | 1;} //定位右孩子,也可以写成 p*2+1private static void bfs(int root) {Queue<Integer> queue = new LinkedList<>(); //定义队列queue.add(root); //第一个节点进入队列while (!queue.isEmpty()) { //用BFS访问二叉树int u = queue.peek(); //读队头,并输出System.out.print(t[u]);queue.poll(); //队头处理完了,弹走if (t[ls(u)] != '\0') queue.add(ls(u)); //左儿子进队列 if (t[rs(u)] != '\0') queue.add(rs(u)); //右儿子进队列 }}public static void main(String[] args) {t[1] = 'A'; //第1层t[2] = 'B'; t[3] = 'C'; //第2层t[4] = 'D'; t[5] = 'E'; t[6] = 'F'; t[7] = 'G'; //第3层t[10] = 'H'; t[14] = 'I'; //第4层bfs(1); //BFS访问二叉树,从根节点1开始。输出:ABCDEFGHISystem.out.println();bfs(3); //BFS访问二叉树的子树,从子节点3开始。输出:CFGI}
}
Python代码
from collections import deque
N = 100
t = [''] * N # 简单地用一个数组定义二叉树
def ls(p): return p << 1 # 定位左孩子,也可以写成 p*2
def rs(p): return (p << 1) | 1 # 定位右孩子,也可以写成 p*2+1
def bfs(root): q = deque() # 定义队列q.append(root) # 第一个节点进入队列while q: # 用BFS访问二叉树u = q.popleft() # 读队头,并弹走print(t[u], end='') # 输出队头if t[ls(u)]: q.append(ls(u)) # 左儿子进队列 if t[rs(u)]: q.append(rs(u)) # 右儿子进队列
t[1] = 'A' # 第1层
t[2] = 'B'; t[3] = 'C' # 第2层
t[4] = 'D'; t[5] = 'E'; t[6] = 'F'; t[7] = 'G' # 第3层
t[10] = 'H';t[14] = 'I' # 第4层
bfs(1) # BFS访问二叉树,从根节点1开始。输出:ABCDEFGHI
print()
bfs(3) # BFS访问二叉树的子树,从子节点3开始。输出:CFGI
2. BFS与最短路径
求最短路径是BFS最常见的应用。
BFS本质上就是一个最短路径算法,因为它由进及远访问节点,先访问到的节点,肯定比后访问到的节点更近。某个节点第一次被访问到的时候,必定是从最短路径走过来的。从起点出发,同一层的节点,到起点的距离都相等。
不过,BFS求最短路有个前提:任意两个邻居节点的边长都相等,把两个邻居节点之间的边长距离称为“一跳”。只有所有边长都相等,才能用BFS的逐层递进来求得最短路。两个节点之间的路径长度,等于这条路径上的边长个数。在这种场景下,BFS是最优的最短路算法,它的计算复杂度只有O(n+m),n是节点数,m是边数。如果边长都不等,就不能用BFS求最短路了,路径长度也不能简单地用边长个数来统计。
下图中,A到B、C、D的最短路长度都是1跳,A到E、F、G、H的最短路都是2跳。
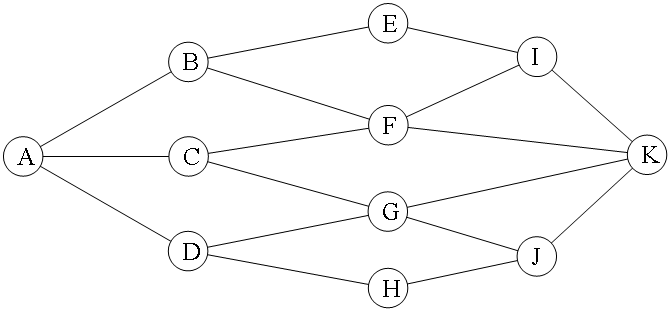
用BFS求最短路路径的题目一般有两个目标:
(1)最短路径的长度。答案唯一,路径长度就是路径经过的边长数量。
(2)最短路径具体经过哪些节点。由于最短路径可能有多条,所以一般不用输出最短路径。如果要输出,一般是输出字典序最小的那条路径。例如上图中,A到F的最短路有两条:A-B-F、A-C-F,字典序最小的是A-B-F。
BFS最短路径的常用的场景是网格图,下面给出一道例题,用这道例题说明如何计算最短路、如何输出路径。
2.1 计算最短路的长度
例题:马的遍历
马走日,从一个坐标点出发,下一步有8种走法。第4、5行用dx[]、dy[]定义下一步的8个方向。设左上角的坐标是(1,1),右下角坐标是(n,m)。
代码的主体部分是标准的BFS,让每个点进出队列。注意如何用队列处理坐标。第24行定义队列,队列元素是坐标struct node。
用dis[][]记录最短路径长度,dis[x][y]是从起点s到(x,y)的最短路径长度。第35行,每扩散一层,路径长度就加1。
C++代码:
#include <bits/stdc++.h>
using namespace std;
struct node{int x,y;}; //定义坐标。左上角(1,1),右下角(n,m)
const int dx[8]={2,1,-1,-2,-2,-1, 1, 2}; //8个方向,按顺时针
const int dy[8]={1,2, 2, 1,-1,-2,-2,-1};
int dis[500][500]; //dis[x][y]: 起点到(x,y)的最短距离长度
int vis[500][500]; //vis[x][y]=1: 已算出起点到坐标(x,y)的最短路
node pre[500][500]; //pre[x][y]:坐标(x,y)的前驱点
void print_path(node s, node t){ //打印路径:从起点s到终点tif(t.x==s.x && t.y==s.y) { //递归到了起点printf("(%d,%d)->",s.x,s.y); //打印起点,返回return;}node p;p.x = pre[t.x][t.y].x; p.y = pre[t.x][t.y].y;print_path(s,p); //先递归回到起点printf("(%d,%d)->",t.x,t.y); //在回溯过程中打印,最后打的是终点
}
int main(){int n,m; node s; cin>>n>>m>>s.x>>s.y;memset(dis,-1,sizeof(dis));dis[s.x][s.y]=0; //起点到自己的距离是0vis[s.x][s.y]=1;queue<node> q;q.push(s); //起点进队while(!q.empty()){node now = q.front();q.pop(); //取队首并出队for(int i=0;i<8;i++) { //下一步可以走8个方向node next;next.x=now.x+dx[i],next.y=now.y+dy[i];if(next.x<1||next.x>n||next.y<1||next.y>m||vis[next.x][next.y])continue; //出界或已经走过vis[next.x][next.y]=1; //标记为已找到最短路dis[next.x][next.y]=dis[now.x][now.y]+1; //计算最短路长度pre[next.x][next.y] = now; //记录点next的前驱是nowq.push(next); //进队列}}for(int i=1;i<=n;i++) {for(int j=1;j<=m;j++)printf("%-5d",dis[i][j]);printf("\n");}// node test; test.x=3; test.y=3; //测试路径打印,样例输入:3 3 1 1,终点(3,3)// print_path(s,test); //输出路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)->return 0;
}
2.2 输出完整的最短路径
本题没有要求打印出具体的路径,不过为了演示如何打印路径,代码中加入了函数print_path(s,t),打印从起点s到终点t的完整路径。第47行打印起点s=(1,1),终点t=(3,3)的完整路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)。如下图虚线箭头所示。

如何记录一条路径?在图上从一个起点s出发做一次BFS,可以求s到其他所有点的最短路。为了记录路径,最简单的方法是每走到一个点i,就在i上把从起点s到i经过的所有点都记下来。例如上图,从(1,1)出发,下一步可以走到(3,2),就在(3,2)上记录”(1,1)->(3,2)”;再走一步可以到(1,3),就在(1,3)上接着记录“(1,1)->(3,2)->(1,3)”;再走一步到(2,1),就在(2,1)上记录“(1,1)->(3,2)->(1,3)->(2,1)”。这样做编程简单,但是浪费空间,因为每个点上都要记录从头到尾的完整路径。
《算法竞赛》123页“3.4 BFS与最短路径”介绍了这两种路径记录方法:简单方法、标准方法。
标准的路径记录方法是:只在点i上记录前驱点,也就是从哪个点走到i的。例如点(1,3),记录它的前驱点是(3,2),(3,2)记录它的前驱点是(1,1)。当需要输出起点(1,1)到(1,3)的完整路径时,只需要从(3,2)倒查回去,就能得到完整路径了。这样做非常节省空间,一个点上只需要记录前一个点就行了。
为什么不在点i上记录它的下一个点?请读者自己思考。
代码第8行用node pre[][]记录路径,pre[x][y]记录了坐标(x,y)的前驱点。按照pre[][]的记录倒查路径上每个点的前一个点,一直查到起点,就得到了完整路径。例如上图,终点为(3,3),pre[3][3]是它的上一个点(2,1);(2,1)的pre[2][1]是它的上一个点(1,3);(1,3)的上一个点是(3,2);(3,2)的上一个点是(1,1),回到了起点。
print_path()打印路径,它是一个递归函数,从终点开始倒查pre[][],一直递归到起点,然后再回溯回终点。在回溯的过程中从起点开始打印路径上的点,就得到了从起点到终点的正序路径。
另外,从起点s到终点t可能有多条最短路径,上面的代码只记录了按顺时针的优先顺序找到的第一条最短路径。第4、5行的dx[]、dy[]按顺时针定义了8个方向,然后在第29行遍历邻居时,也是按dx[]、dy[]的顺序,那么得到的最短路径就是按顺时针的。
Java代码:
import java.util.*;
class Main {static class Node { //定义坐标。左上角(1,1),右下角(n,m)int x, y;Node(int x, int y) {this.x = x;this.y = y;}}public static void printPath(Node s, Node t, Node[][] pre){ //打印路径:起点s终点tif (t.x == s.x && t.y == s.y) { //递归到了起点System.out.print("(" + s.x + "," + s.y + ")->"); //打印起点,然会回溯return;}Node p = pre[t.x][t.y];printPath(s, p, pre); //先递归回到起点System.out.print("(" + t.x + "," + t.y + ")->"); //回溯打印,最后打的是终点}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();Node s = new Node(scanner.nextInt(), scanner.nextInt());int[][] dis = new int[n+1][m+1]; //dis[x][y]:起点到(x,y)的最短距离长度int[][] vis = new int[n+1][m+1]; //vis[x][y]=1:已算出起点到坐标(x,y)的最短路Node[][] pre = new Node[n + 1][m + 1]; //pre[x][y]:坐标(x,y)的前驱点int[] dx = {2, 1, -1, -2, -2, -1, 1, 2}; //8个方向,按顺时针int[] dy = {1, 2, 2, 1, -1, -2, -2, -1};for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)dis[i][j] = -1;dis[s.x][s.y] = 0; //起点到自己的距离是0vis[s.x][s.y] = 1;Queue<Node> queue = new LinkedList<>();queue.add(s); //起点进队while (!queue.isEmpty()) {Node now = queue.poll(); //取队首并出队for (int i = 0; i < 8; i++) {int nx = now.x + dx[i];int ny = now.y + dy[i];if (nx < 1 || nx > n || ny < 1 || ny > m || vis[nx][ny] == 1) continue; //出界或已经走过vis[nx][ny] = 1; //标记为已找到最短路dis[nx][ny] = dis[now.x][now.y] + 1; //计算最短路长度pre[nx][ny] = now; //记录点next的前驱是nowqueue.add(new Node(nx, ny));//进队列}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) System.out.printf("%-5d", dis[i][j]); System.out.println();}// Node test = new Node(3, 3); //测试路径打印,样例输入:3 3 1 1,终点(3,3)// printPath(s, test, pre); //输出路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)->}
}
Python代码
from collections import deque
dx = [2, 1, -1, -2, -2, -1, 1, 2] #8个方向,按顺时针
dy = [1, 2, 2, 1, -1, -2, -2, -1]
class Node: #定义坐标。左上角(1,1),右下角(n,m)def __init__(self, x, y):self.x = xself.y = y
def print_path(s, t, pre): #打印路径:从起点s到终点tif t.x == s.x and t.y == s.y: #递归到了起点print(f"({s.x},{s.y})->", end="") #打印起点,返回returnp = pre[t.x][t.y] print_path(s, p, pre) #先递归回到起点print(f"({t.x},{t.y})->", end="") #在回溯过程中打印,最后打的是终点
def main():n, m,u,v = map(int, input().split())s = Node(u,v)dis = [[-1] * (m+1) for _ in range(n+1)] #dis[x][y]: 起点到(x,y)的最短距离长度vis = [[0] * (m+1) for _ in range(n+1)] #vis[x][y]=1: 已算出起点到(x,y)的最短路pre = [[None] * (m+1) for _ in range(n+1)] #pre[x][y]: 坐标(x,y)的前驱点dis[s.x][s.y] = 0 #起点到自己的距离是0vis[s.x][s.y] = 1q = deque([s]) #起点进队while q: now = q.popleft() #取队首并出队for i in range(8): #下一步可以走8个方向nx, ny = now.x + dx[i], now.y + dy[i]if nx<1 or nx>n or ny < 1 or ny > m or vis[nx][ny]:continue #出界或已经走过vis[nx][ny] = 1 #标记为已找到最短路dis[nx][ny] = dis[now.x][now.y] + 1 #计算最短路长度pre[nx][ny] = now #记录点(nx,ny)的前驱是nowq.append(Node(nx, ny)) #进队列for i in range(1, n + 1):for j in range(1, m + 1):print(f"{dis[i][j]:-5d}", end="")print() #test = Node(3, 3) #测试路径打印,样例输入:3 3 1 1,终点(3,3)#print_path(s, test, pre) #输出路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)->
if __name__ == "__main__":main()
3. BFS与判重
BFS的题目往往需要“判重”。BFS的原理是逐层扩展,把扩展出的下一层点(或称为状态)放进队列中。
在任意时刻,队列中只包含相邻两层的点。只有两层,看起来似乎不多,但是很多情况下是个极大的数字。例如一棵满二叉树,第25层的点就有225≈3000万个,队列放不下。
不过在很多情况下,其实状态的总数量并不多,在层层扩展过程中,很多状态是重复的,没有必要重新放进队列。这产生了判重的需求。
用下面的题目说明判重的原理和编程方法。
例题:九宫重排
题目求从初态到终态的最少步数,是典型的BFS最短路路径问题。
让卡片移动到空格比较麻烦,改为让空格上下左右移动,就简单多了。空格的每一步移动,可能有2、3、4种新局面,如果按3种算,移动到第15步,就有315>1千万种局面,显然队列放不下。不过,其实局面总数仅有9!=362880种,队列放得下,只要判重,不让重复的局面进入队列即可。
3.1 C++判重
判重可以用STL map或set。(1)map判重。map是STL容器,存放键值对。键有唯一性,键和值有一一对应关系。由于每个键是独一无二的,可以用来判重。map的基本用法见下面的例子。
#include <bits/stdc++.h>
using namespace std;
int main(){map<string,int> mp{{"tom",78},{"john",92},{"rose",83}}; //三个键值对cout << mp["tom"]<<"\n"; //输出 78cout << mp.count("tom")<<"\n"; //检查map中是否有"tom"。输出 1mp["white"]=100; //加入新键值对,键是"white",值是100cout << mp["white"]<<"\n"; //输出 100cout << mp.count("sam")<<"\n"; //查不到键,输出 0map<int, int> mp2{{2301,89},{2302,98}}; cout << mp2[2301]<<"\n"; //输出 89map<int, string> mp3{{301,"dog"},{232,"pig"}};cout << mp3[232]<<"\n"; //输出 pigreturn 0;
}
map容器中提供了count()用于统计键的个数,有键返回1,没有键返回0。count()可以用来判重:若某个键的count()等于1,说明这个键已经在map中,不用再放进map。
下面给出本题的C++代码。第22行判重,判断局面tmp是否曾经处理过,第23行把新局面tmp放进map。
#include <bits/stdc++.h>
using namespace std;
int dx[] = {-1, 0, 1, 0}; //上下左右四个方向
int dy[] = { 0, 1, 0, -1};
map <string,int> mp;
int bfs(string s1,string s2){queue<string>q;q.push(s1);mp[s1]=0; //mp[s1]=0表示s1到s1的步数是0。另外:mp.count(s1)=1while(q.size()){string ss = q.front();q.pop();int dist = mp[ss]; //从s1到ss的移动步数if(ss==s2) return dist; //到达终点,返回步数int k=ss.find('.'); //句点的位置int x=k/3,y=k%3; //句点坐标:第x行、第y列for(int i=0;i<4;i++){int nx=x+dx[i], ny=y+dy[i]; //让句点上下左右移动if(nx<0 || ny<0 || nx>2 || ny>2) continue; //越界string tmp=ss;swap(tmp[k],tmp[nx*3+ny]); //移动if(mp.count(tmp)==0){ //判重,如果tmp曾经处理过,就不再处理mp[tmp] = dist+1; //把tmp放进map,并赋值。mp[tmp]等于s1到tmp的步数q.push(tmp);}}}return -1; //没有找到终态局面,返回-1
}
int main(){string s1,s2; cin>>s1>>s2; //初态局面s1,终态局面s2cout<<bfs(s1,s2);return 0;
}
(2)set判重。set是STL的常用容器,set中的元素是有序的且具有唯一性,利用这个特性,set常用来判重。set的基本用法见下面的例子。
#include <bits/stdc++.h>
using namespace std;
int main() {set<string>st{"111","222","33"}; // 定义 set,插入初值if(st.count("111")) cout <<1; //有"111",输出 1else cout <<-1;cout<<"\n";if(st.count("44")) cout <<4;else cout <<-4; //无"44",输出 -4cout <<"\n";st.insert("44"); //插入"44"if(st.count("44")) cout <<4; //有"44",输出 4return 0;
}
本题用set判重的代码:
#include <bits/stdc++.h>
using namespace std;
int dx[] = {-1, 0, 1, 0}; //上下左右四个方向
int dy[] = { 0, 1, 0, -1};
struct node{node(string ss, int tt){s=ss, t=tt;}string s; //局面int t; //到这个局面的步数
};
set <string> st; //用set st判重
int bfs(string s1,string s2){queue<node>q;q.push(node(s1,0));st.insert(s1);while(q.size()){node now = q.front();q.pop();string ss = now.s;int dist = now.t; //从s1到ss的移动步数if(ss==s2) return dist; //到达终点,返回步数int k=ss.find('.'); //句点的位置int x=k/3,y=k%3; //句点坐标:第x行、第y列for(int i=0;i<4;i++){int nx=x+dx[i], ny=y+dy[i]; //让句点上下左右移动if(nx<0 || ny<0 || nx>2 || ny>2) continue; //越界string tmp=ss;swap(tmp[k],tmp[nx*3+ny]); //移动if(st.count(tmp)==0){ //判重,如果tmp曾经处理过,就不再处理st.insert(tmp);q.push(node(tmp,dist+1));}}}return -1; //没有找到终态局面,返回-1
}
int main(){string s1,s2; cin>>s1>>s2; //初态局面s1,终态局面s2cout<<bfs(s1,s2);return 0;
}
3.2 Java判重
(1)用map判重
import java.util.*;
public class Main {static int[] dx = {-1, 0, 1, 0}; // 上下左右四个方向static int[] dy = {0, 1, 0, -1};static Map<String, Integer> mp;public static int bfs(String s1, String s2) {Queue<String> q = new LinkedList<>();q.add(s1);mp.put(s1, 0); // 0表示s1到s1的步数是0while (!q.isEmpty()) {String ss = q.poll();int dist = mp.get(ss); // 从s1到ss的移动步数if (ss.equals(s2)) return dist; // 到达终点,返回步数int k = ss.indexOf('.'); // 句点的位置int x = k / 3, y = k % 3; // 句点坐标:第x行、第y列for (int i = 0; i < 4; i++) {int nx = x + dx[i], ny = y + dy[i]; // 让句点上下左右移动if (nx < 0 || ny < 0 || nx > 2 || ny > 2) continue; // 越界StringBuilder tmp = new StringBuilder(ss);tmp.setCharAt(k, tmp.charAt(nx * 3 + ny)); // 移动tmp.setCharAt(nx * 3 + ny, '.');if (!mp.containsKey(tmp.toString())) {//判重,如果tmp处理过,就不再处理mp.put(tmp.toString(), dist + 1); //把tmp放进map,并赋值为步数q.add(tmp.toString());}}}return -1; // 没有找到终态局面,返回-1}public static void main(String[] args) {mp = new HashMap<>();Scanner scanner = new Scanner(System.in);String s1 = scanner.next();String s2 = scanner.next();System.out.println(bfs(s1, s2));}
}
(2)用set判重
import java.util.*;
public class Main {static int[] dx = {-1, 0, 1, 0}; // 上下左右四个方向static int[] dy = {0, 1, 0, -1};static Set<String> st;static class Node {String s; // 局面int t; // 到这个局面的步数public Node(String ss, int tt) {s = ss;t = tt;}}public static int bfs(String s1, String s2) {Queue<Node> q = new LinkedList<>();q.add(new Node(s1, 0));st.add(s1);while (!q.isEmpty()) {Node now = q.poll();String ss = now.s;int dist = now.t; // 从s1到ss的移动步数if (ss.equals(s2)) return dist; // 到达终点,返回步数int k = ss.indexOf('.'); // 句点的位置int x = k / 3, y = k % 3; // 句点坐标:第x行、第y列for (int i = 0; i < 4; i++) {int nx = x + dx[i], ny = y + dy[i]; // 让句点上下左右移动if (nx < 0 || ny < 0 || nx > 2 || ny > 2) continue; // 越界StringBuilder tmp = new StringBuilder(ss);tmp.setCharAt(k, tmp.charAt(nx * 3 + ny)); // 移动tmp.setCharAt(nx * 3 + ny, '.');if (!st.contains(tmp.toString())) {//判重,如果tmp处理过,就不再处理st.add(tmp.toString());q.add(new Node(tmp.toString(), dist + 1));}}}return -1; // 没有找到终态局面,返回-1}public static void main(String[] args) {st = new HashSet<>();Scanner scanner = new Scanner(System.in);String s1 = scanner.next();String s2 = scanner.next();System.out.println(bfs(s1, s2));}
}
3.3 Python判重
(1)用set判重
from collections import deque
dx = [-1, 0, 1, 0] # 上下左右四个方向
dy = [0, 1, 0, -1]
class Node:def __init__(self, s, t):self.s = s # 局面self.t = t # 到这个局面的步数
def bfs(s1, s2):q = deque()q.append(Node(s1, 0))st = set()st.add(s1)while q:now = q.popleft()ss = now.sdist = now.t # 从s1到ss的移动步数if ss == s2: return dist # 到达终点,返回步数k = ss.index('.')x = k // 3y = k % 3for i in range(4):nx = x + dx[i]ny = y + dy[i]if nx < 0 or ny < 0 or nx > 2 or ny > 2: continue # 越界tmp = list(ss)tmp[k], tmp[nx * 3 + ny] = tmp[nx * 3 + ny], tmp[k] # 移动tmp = ''.join(tmp)if tmp not in st: # 判重,如果tmp曾经处理过,就不再处理st.add(tmp)q.append(Node(tmp, dist + 1))return -1 # 没有找到终态局面,返回-1
s1 = input() # 初态局面s1
s2 = input() # 终态局面s2
print(bfs(s1, s2))
(2)用字典判重
from collections import deque
dx = [-1, 0, 1, 0] # 上下左右四个方向
dy = [0, 1, 0, -1]
def bfs(s1, s2):q = deque()q.append(s1)mp = {s1: 0} # 定义字典。mp[s1]=0表示s1到s1的步数是0 while q:ss = q.popleft()dist = mp[ss] # 从s1到ss的移动步数if ss == s2: return dist # 到达终点,返回步数k = ss.find('.')x = k // 3y = k % 3for i in range(4):nx = x + dx[i]ny = y + dy[i]if nx < 0 or ny < 0 or nx > 2 or ny > 2: continue # 越界tmp = list(ss)tmp[k], tmp[nx * 3 + ny] = tmp[nx * 3 + ny], tmp[k] # 移动tmp = ''.join(tmp)if tmp not in mp: # 判重,如果tmp曾经处理过,就不再处理mp[tmp] = dist + 1 # 把tmp放进map,并赋值。mp[tmp]等于s1到tmp的步数q.append(tmp)return -1 # 没有找到终态局面,返回-1
s1 = input() # 初态局面s1
s2 = input() # 终态局面s2
print(bfs(s1, s2))
习题:
洛谷搜索提单:https://www.luogu.com.cn/training/112#problems






)










--谈谈从GBK转到GB18030的特殊情况)

