初步理解
这里看看就好
熵权法是一种常用的多指标综合评价方法,通过计算指标的熵值来确定各指标的权重。而Topsis模型则是一种常用的多指标决策模型,用于评估不同方案的优劣。
在基于熵权法的Topsis模型中,可以对熵权法进行一些修正来提高模型的准确性和可靠性。以下是一种可能的修正方法:
1. 引入相对熵值:在熵权法中,计算指标的熵值时使用的是绝对熵值,即每个指标的熵值都是相互独立计算的。然而,在实际问题中,不同指标之间常常存在一定的相关性。为了更准确地反映指标的信息量,可以引入相对熵值的概念,即考虑各指标之间的相关性。通过计算指标之间的协方差矩阵,可以得到各指标的相关性系数,然后将相关性系数考虑到熵值的计算中,得到相对熵值。
2. 建立模型的一致性检验:在Topsis模型中,评估方案的优劣是通过计算方案与理想解之间的距离来实现的。然而,在使用Topsis模型时,往往会使用专家判断或者模糊评价来确定指标的权重和方案的评价等级。这样会引入主观因素,可能导致模型的不一致性。为了保证模型的一致性和可靠性,可以建立模型的一致性检验步骤,对模型进行检验和验证。
3. 敏感性分析:在Topsis模型中,通过调整指标的权重来评估不同方案的优劣。然而,指标权重的确定往往是主观的,并且可能会受到多个因素的影响。为了克服这些问题,可以引入敏感性分析的方法,通过对不同权重组合下的模型结果进行分析,来确定最优的权重组合。
通过以上修正方法,可以提高基于熵权法的Topsis模型的准确性和可靠性,使其更适用于实际决策问题。
引入

如何度量信息量的大小
小张和小王是两个高中生。小张学习很差,而小王是全校前几名的尖子生。
高考结束后,小张和小王都考上了清华。小王考上了清华,大家都会觉得很正常,里
面没什么信息量,因为学习好上清华,天经地义,本来就应该如此的事情。
然鹅,如果是小张考上了清华,这就不一样了,这里面包含的信息量就非常大。怎么
说?因为小张学习那么差,怎么会考上清华呢?把不可能的事情变成可能,这里面就有很
多信息量。
注:本例子来自微信公众号:“小宇治水”
上面的小例子告诉我们:
越有可能发生的事情,信息量越少,
越不可能发生的事情,信息量就越多。
那么怎么衡量事情发生的可能性大小?
答:概率越大信息量越小

信息熵的定义

熵越大信息量越大还是越小

熵越大,信息量越小
熵权法的计算步骤

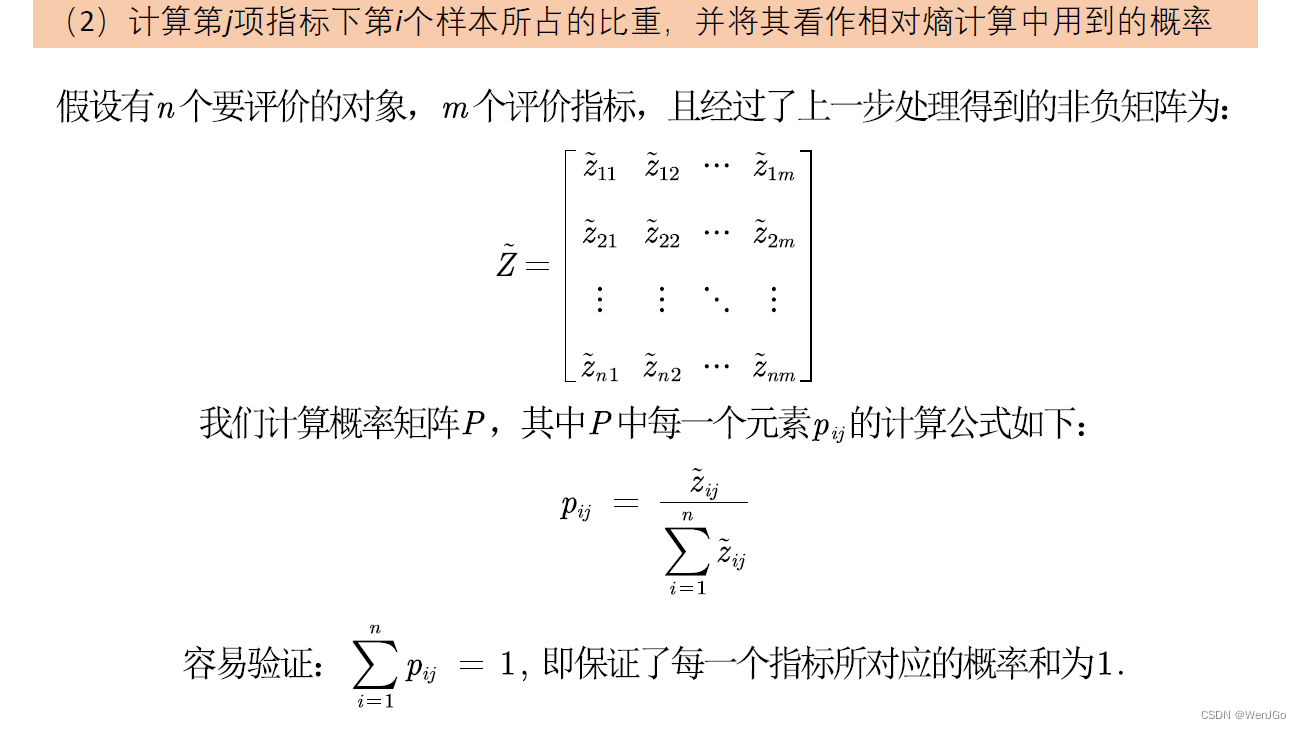

熵权法背后的原理

熵权法的讨论
熵权法的另一个问题:
因为概率p是位于0‐1之间,因此需要对原始数据进行标准化,我们应该选择哪种方式进行标准化呢?查看知网的文献会发现,
并没有约定俗成的标准,每个人的选取可能都不一样。但是不同方式标准化得到的结果
可能有很大差异,所以说熵权法也是存在着一定的问题的。
也就是说:
如果大家的论文要发表,别用熵权法
如果大家只是用这个方法进行比赛
那么可以随便用
因为这个方法总比你自己随意定义好
熵权法的代码实现
function [W] = Entropy_Method(Z)
% 计算有n个样本,m个指标的样本所对应的的熵权
% 输入
% Z : n*m的矩阵(要经过正向化和标准化处理,且元素中不存在负数)
% 输出
% W:熵权,1*m的行向量
代码
Entropy_Method
function [W] = Entropy_Method(Z)
% 计算有n个样本,m个指标的样本所对应的的熵权
% 输入
% Z : n*m的矩阵(要经过正向化和标准化处理,且元素中不存在负数)
% 输出
% W:熵权,1*m的行向量%% 计算熵权[n,m] = size(Z);D = zeros(1,m); % 初始化保存信息效用值的行向量for i = 1:mx = Z(:,i); % 取出第i列的指标p = x / sum(x);% 注意,p有可能为0,此时计算ln(p)*p时,Matlab会返回NaN,所以这里我们自己定义一个函数e = -sum(p .* mylog(p)) / log(n); % 计算信息熵D(i) = 1- e; % 计算信息效用值endW = D ./ sum(D); % 将信息效用值归一化,得到权重
endmylog
% 重新定义一个mylog函数,当输入的p中元素为0时,返回0
function [lnp] = mylog(p)
n = length(p); % 向量的长度
lnp = zeros(n,1); % 初始化最后的结果for i = 1:n % 开始循环if p(i) == 0 % 如果第i个元素为0lnp(i) = 0; % 那么返回的第i个结果也为0elselnp(i) = log(p(i)); endend
endtopsis
%% 第一步:把数据复制到工作区,并将这个矩阵命名为X
% (1)在工作区右键,点击新建(Ctrl+N),输入变量名称为X
% (2)在Excel中复制数据,再回到Matlab中右键,点击粘贴Excel数据(Ctrl+Shift+V)
% (3)关掉这个窗口,点击X变量,右键另存为,保存为mat文件(下次就不用复制粘贴了,只需使用load命令即可加载数据)
% (4)注意,代码和数据要放在同一个目录下哦。
clear;clc
load data_water_quality.mat%% 第二步:判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标'])
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0: ']);if Judge == 1Position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: '); %[2,3,4]disp('请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ')Type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: '); %[2,1,3]% 注意,Position和Type是两个同维度的行向量for i = 1 : size(Position,2) %这里需要对这些列分别处理,因此我们需要知道一共要处理的次数,即循环的次数X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));% Positivization是我们自己定义的函数,其作用是进行正向化,其一共接收三个参数% 第一个参数是要正向化处理的那一列向量 X(:,Position(i)) 回顾上一讲的知识,X(:,n)表示取第n列的全部元素% 第二个参数是对应的这一列的指标类型(1:极小型, 2:中间型, 3:区间型)% 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列% 该函数有一个返回值,它返回正向化之后的指标,我们可以将其直接赋值给我们原始要处理的那一列向量enddisp('正向化后的矩阵 X = ')disp(X)
end
%% 作业:在这里增加是否需要算加权
% 补充一个基础知识:m*n维的矩阵A 点乘 n维行向量B,等于这个A的每一行都点乘B
% (注意:2017以及之后版本的Matlab才支持,老版本Matlab会报错)
% % 假如原始数据为:
% A=[1, 2, 3;
% 2, 4, 6]
% % 权重矩阵为:
% B=[ 0.2, 0.5 ,0.3 ]
% % 加权后为:
% C=A .* B
% 0.2000 1.0000 0.9000
% 0.4000 2.0000 1.8000
% 类似的,还有矩阵和向量的点除, 大家可以自己试试计算A ./ B
% 注意,矩阵和向量没有 .- 和 .+ 哦 ,大家可以试试,如果计算A.+B 和 A.-B会报什么错误。%% 这里补充一个小插曲
% % 在上一讲层次分析法的代码中,我们可以优化以下的语句:
% % Sum_A = sum(A);
% % SUM_A = repmat(Sum_A,n,1);
% % Stand_A = A ./ SUM_A;
% % 事实上,我们把第三行换成:Stand_A = A ./ Sum_A; 也是可以的哦
% % (再次强调,新版本的Matlab才能运行哦)%% 第三步:对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)%% 让用户判断是否需要增加权重
disp("请输入是否需要增加权重向量,需要输入1,不需要输入0")
Judge = input('请输入是否需要增加权重: ');
if Judge == 1Judge = input('使用熵权法确定权重请输入1,否则输入0: ');if Judge == 1if sum(sum(Z<0)) >0 % 如果之前标准化后的Z矩阵中存在负数,则重新对X进行标准化disp('原来标准化得到的Z矩阵中存在负数,所以需要对X重新标准化')for i = 1:nfor j = 1:mZ(i,j) = [X(i,j) - min(X(:,j))] / [max(X(:,j)) - min(X(:,j))];endenddisp('X重新进行标准化得到的标准化矩阵Z为: ')disp(Z)endweight = Entropy_Method(Z);disp('熵权法确定的权重为:')disp(weight)elsedisp(['如果你有3个指标,你就需要输入3个权重,例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);weight = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);OK = 0; % 用来判断用户的输入格式是否正确while OK == 0 if abs(sum(weight) -1)<0.000001 && size(weight,1) == 1 && size(weight,2) == m % 注意,Matlab中浮点数的比较要小心OK =1;elseweight = input('你输入的有误,请重新输入权重行向量: ');endendend
elseweight = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同,即都为1/m
end%% 第四步:计算与最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')% A = magic(5) % 幻方矩阵
% M = magic(n)返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。阶次n必须为大于或等于3的标量。
% sort(A)若A是向量不管是列还是行向量,默认都是对A进行升序排列。sort(A)是默认的升序,而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵,默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A)
% dim=2时表示对A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中给一维向量排序是使用sort函数:sort(A),排序是按升序进行的,其中A为待排序的向量;
% 若欲保留排列前的索引,则可用 [sA,index] = sort(A,'descend') ,排序后,sA是排序好的向量,index是向量sA中对A的索引。
% sA = 8 3 2 1
% index = 4 3 1 2运行结果

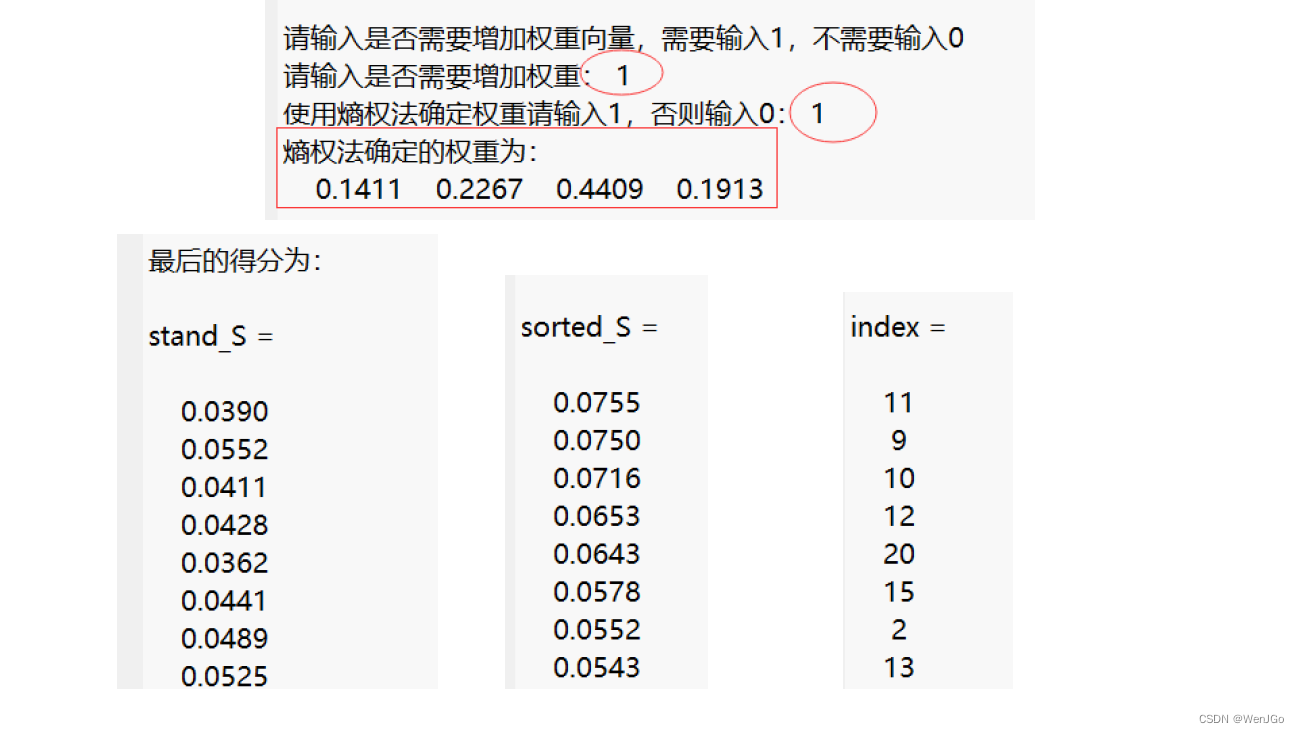
总结
打比赛可以用,写论文发表还是且行且珍惜呀~~

—— 按键中断驱动)


)












 => m.Id - n.Id); id是double类型的为什么回报错)
:优选算法详解)
