目录
- 前言
- 一、浮点数存储例子
- 二、浮点数在内存的存储格式
- 2.1 32位浮点数存储格式
- 2.2 64位浮点数存储格式
- 三、IEEE 754对有效数字M和指数E的规定
- 3.1 对存储有效数字M的规定
- 3.2 对存储指数E的规定
- 3.2.1 E在32位浮点数的存储格式
- 3.2.2 E在64位浮点数的存储格式
- 3.3 对读取有效数M和指数E的规定
- 3.3.1 当E在内存存储的值不全为0或不全为1
- 3.3.2 当E在内存存储的值为全0时
- 3.3.3 当E在内存存储的值为全1时
- 总结
前言
本篇文章介绍浮点型数据在内存中的存储。
一、浮点数存储例子
浮点型家族
- float
- double
- long double(c99)
…
浮点数表示的范围在<float.h>头文件中定义
整型家族表示范围在<limits.h>头文件中定义
例子演示:
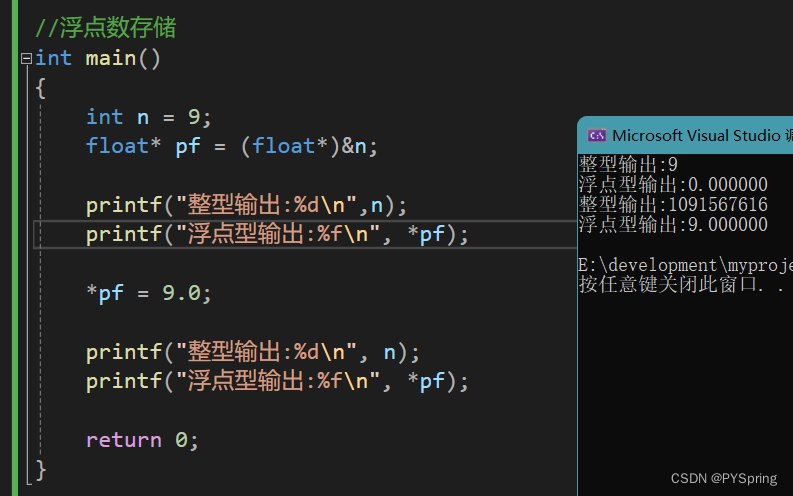
结果分析:
使用一个float指针指向整型变量n,按浮点型输出时,输出了0;
通过float指针改变指针指向的内容,按整型输出时,输出了一个非常大的正整数。
说明整型数据和浮点型数据的存储和对数据的访问方式不相同。
下面对浮点型数据的存储展开叙述。
二、浮点数在内存的存储格式
根据国际标准IEEE754,任意一个二进制浮点数V可以写成:
浮点数公式:(-1)^S * M * 2^E
S表示符号位,0表示正数,1表示负数;
M表示有效数字, 1 <= M < 2;
E表示指数位
例子1:
假设一个十进制浮点数V = 5.0f,化成二进制为101.0
根据二进制科学计数法,101.0 -> 1.01 * (2 ^ 2)-> (-1)^0 * 1.01 * (2^2)
则此时S = 0、M = 1.01、E = 2
例子2:
假设一个十进制浮点数V = 9.5f,化成二进制为1001.1
根据二进制科学计数法,1001.1->1.0011 * (2 ^ 3) -> (-1)^0 * 1.0011 * (2^3)
则此时S = 0、M = 1.0011、E = 3
2.1 32位浮点数存储格式
S占1bit、E占8bit、M占23bit

2.2 64位浮点数存储格式
S占1bit、E占11bit、M占52bit

三、IEEE 754对有效数字M和指数E的规定
3.1 对存储有效数字M的规定
1 <= M < 2,则M可以写成1.xxx的形式,其中xxx表示小数部分。
IEEE 754规定,在计算机内部存储M时,默认M的第一个位总是1,因此在存储M时,不会将这个1存储,只存储小数部分。比如M = 1.01时,只存储01,当读取时,再自动加上1。
好处:可以节省一个有效位,即23位都存储小数部分。
3.2 对存储指数E的规定
科学计数法中的E会出现负数,可以IEEE754规定,存入内存的值为E的真实值再加上一个中间值
下面根据不同位数进行叙述:
3.2.1 E在32位浮点数的存储格式
E的取值范围:0~255
E的中间值:127
存储值 = 真实值+中间值
例如:
当一个浮点数的指数为2^10时,E的真实值为10,则存储值 = 10 + 127 = 137,即10001001,不够23位,用0补齐
则M在内存的表示为 1000 1001 0000 0000 0000 000
3.2.2 E在64位浮点数的存储格式
E的取值范围:0~2047
E的中间值:1023
存储值 = 真实值+中间值
3.3 对读取有效数M和指数E的规定
3.3.1 当E在内存存储的值不全为0或不全为1
指数E的存储值-中间值(127或1023),得到真实值,然后在有效位M前加上第一位。
3.3.2 当E在内存存储的值为全0时
浮点数的指数E的真实值 = (1 - 127) 或 (1-1023)
有效数字M不再加上第一位1,而是还原为0.xxx的小数。
这样做是为了表示正负0,以及接近于0的很小的数。
3.3.3 当E在内存存储的值为全1时
这时,如果有效数字M全为1,表示正负无穷大(正负取决于符号位S)
总结
本篇文章叙述了浮点型数据在内存中的存储格式。








)






)



![[情商-6]:识别职场中、情侣之间的暗捧、暗拍、暗赞、暗赏,保持良好的关系](http://pic.xiahunao.cn/[情商-6]:识别职场中、情侣之间的暗捧、暗拍、暗赞、暗赏,保持良好的关系)