文章目录
- 3D数学基础
- 矢量/向量
- 概述 - 什么是向量
- 单位矢量:只关注方向不关注大小
- 数学运算
- 矢量的加法与减法
- 减法的几何意义计算一个点到另一个点的位移
- 矢量的点积与叉积
- 矩阵
- 矩阵的几何意义
3D数学基础
矢量/向量
在笔记中
- 变量使用小写字母表示,a
- 由于笔记中画上箭头表示向量比较麻烦,这里小写字母加粗显示,a
- 矩阵变量使用粗体大写字母表示,A
概述 - 什么是向量
在线性代数中,
Vector被称为向量。在几何中,Vector被称为矢量。
向量意义
对数学家来说,向量是一个数字列表(程序员一般称为数组)。
[1,2,3]表示为行向量,垂直过来就是列向量。可以引用向量来表示各个分量,通常使用x,y来代指二维向量中的元素,x,y,z来代指三维向量中的元素。比如a=[1,2,3]中ax=1,ay=2,az=3
矢量意义
矢量是具有大小和方向的有向线段
- 矢量的大小:矢量的长度,非负值。
- 矢量的方向:描述矢量在空间中指向的方向。
图形上每个矢量是位置无关的,比如使用笛卡尔坐标描述矢量时,每个坐标相当于描述对应维度(x、y或其他)中有符号位移。
比如三维矢量[3,-1,2]可以表示为①向+x轴平移3个单位②向+y轴平移-1个单位(或者-y轴平移1个单位)③向+z轴平移2个单位。其实顺序不重要,移动的总量是一样的。
零矢量:矢量中唯一没有方向的,可以理解为无位移(而不是一个点因为矢量不描述一点)
点与矢量的关系
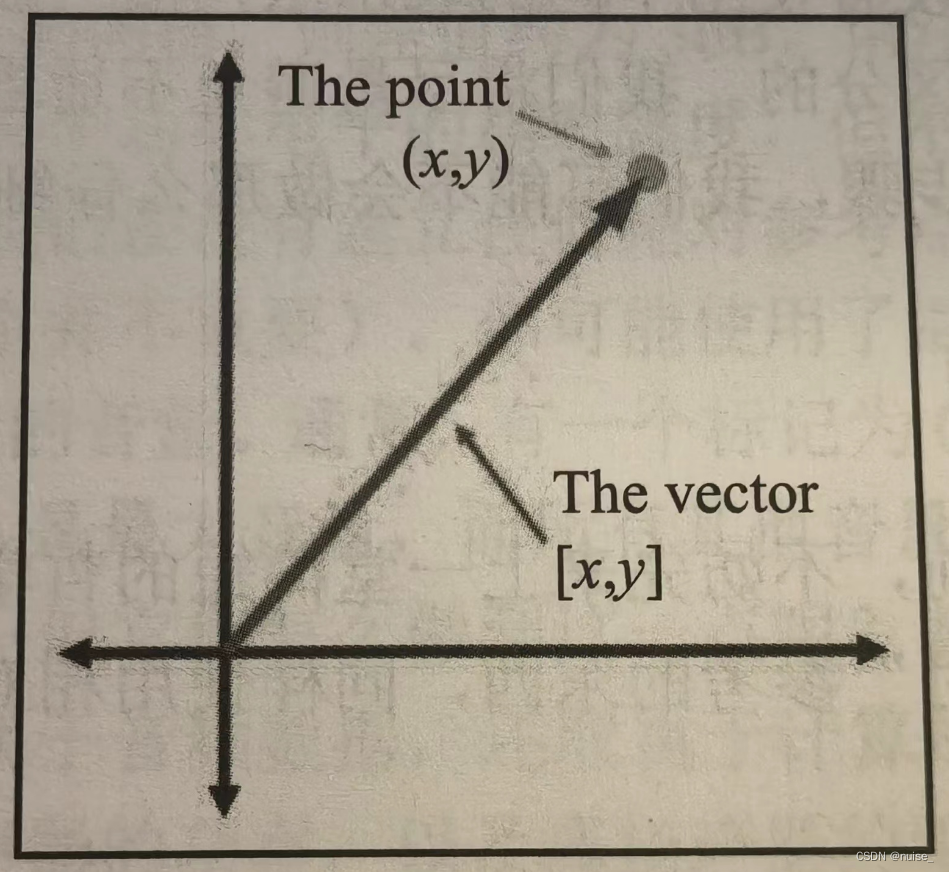
假设有点(x,y)与矢量[x,y]
如果从原点开始按照矢量[x,y]指定的量移动,最终将到达点(x,y)的位置。或者说矢量[x,y]给出了原点到点(x,y)的位移。
单位矢量:只关注方向不关注大小
单位矢量/归一化矢量 表示大小为1(单位长度)的矢量
有时会将单位向量称为法线,法线通常隐含垂直于其他东西的矢量,主要关注点在垂直而不是单位长度。法线往往是单位向量,但是也有例外(所以需要注意例外的情况)
总结
- 归一化矢量是大小为单位长度的矢量
- 法线与某些东西垂直的矢量,通常情况是单位长度
计算公式
v的单位矢量=v/|v|
数学运算
标量和矢量的乘法,标量乘以矢量的每个分量
k[x,y,z] = [x,y,z]k = [kx,ky,kz]
矢量的加法与减法
规则:相应分量相加/相减
a+b= b+a
a-b = -(b-a)
比如a+b,三角形法则几何理解为从一个点开始应用由a指定的位移,然后再应用由b指定的位移
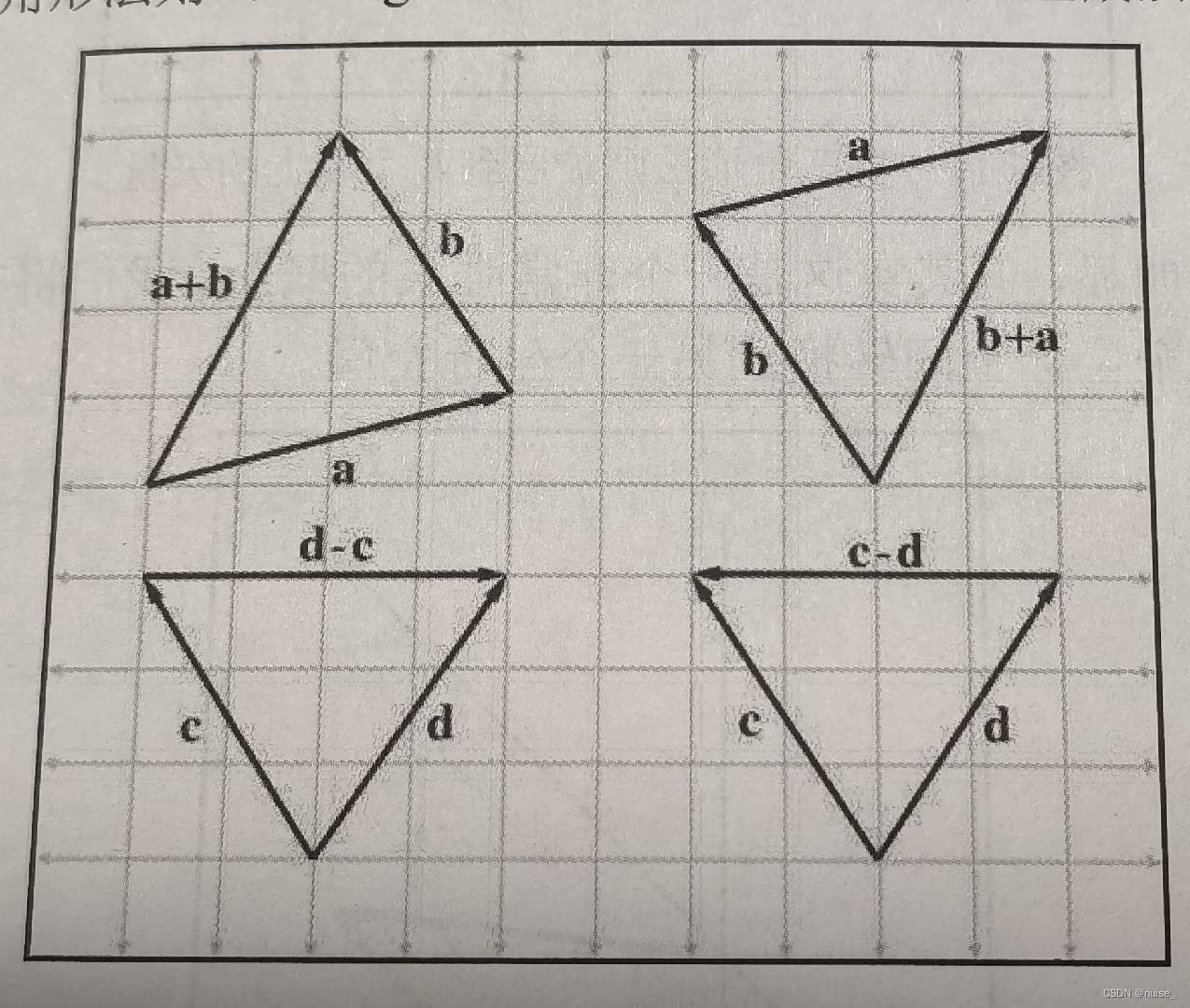
减法的几何意义计算一个点到另一个点的位移
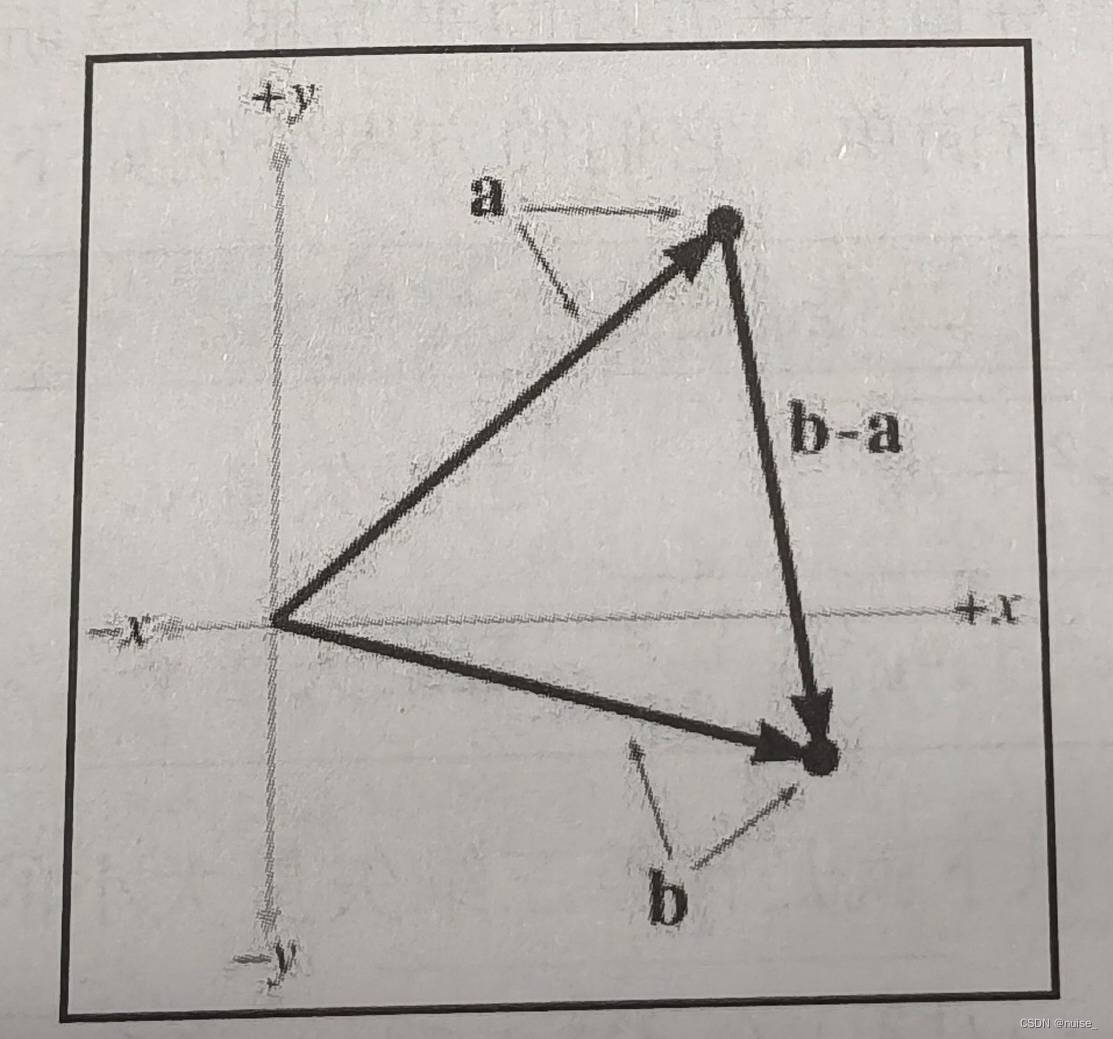
比如a点到b的距离,将ab理解为来自原点的矢量,b-a产生的是从a到b的矢量,矢量b-a的长度就是两点之间的距离。
矢量的点积与叉积


矩阵


矩阵的几何意义
- 方阵的行可以理解为坐标空间的基矢量
- 将矢量从原始空间变化到新坐标空间的方法是:
矢量 * 矩阵 - 原始坐标空间到由基矢量定义的坐标空间的变化是线性变化(保留直线、平行线也保持平行、原点不移动
变化不包含平移),但角度、长度、面积等可能在变化后发生变化。 - 可以通过可视化变化后坐标空间的基矢量来可视化矩阵。




)





FDBAQ压缩算法详解)






)

