💗💗💗欢迎来到我的博客，你将找到有关如何使用技术解决问题的文章，也会找到某个技术的学习路线。无论你是何种职业，我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章，也欢迎在文章下方留下你的评论和反馈。我期待着与你分享知识、互相学习和建立一个积极的社区。谢谢你的光临，让我们一起踏上这个知识之旅！

🍋贝叶斯定理简介

贝叶斯分类基于贝叶斯定理，其核心思想是通过先验概率和样本数据计算后验概率，从而进行分类。贝叶斯定理表达为：

其中，P(A∣B) 是在给定观测数据 B 的情况下事件 A 的后验概率，P(B∣A) 是在事件 A发生的情况下观测到 B 的概率，P(A) 是事件 A 的先验概率，P(B) 是观测到 B 的概率。

🍋贝叶斯分类器

基本原理

贝叶斯分类器基于贝叶斯定理构建，对于给定的输入样本，计算每个类别的后验概率，选择具有最高后验概率的类别作为最终分类结果。

其中，Likelihood 是给定类别的样本条件下观测到输入数据的概率，Prior 是类别的先验概率，Evidence 是观测到输入数据的概率。

🍋朴素贝叶斯分类器

朴素贝叶斯分类器是贝叶斯分类中的一种常见形式，它假设输入特征之间相互独立，简化了计算。对于给定的输入 X=(x1,x2,…,xn)，朴素贝叶斯分类器的决策规则为：

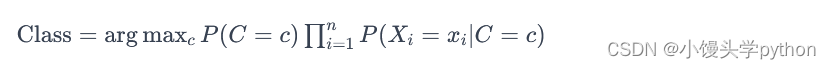
其中，P(C=c) 是类别 c 的先验概率，P(Xi​=xi​∣C=c) 是在给定类别 c 的情况下特征 Xi​ 的条件概率。

🍋优势与不足

优势

• 简单有效： 贝叶斯分类器具有简单的理论基础，易于实现。
• 处理小样本数据： 在数据较少的情况下仍然有效，特别适用于小样本场景。
• 对噪声数据不敏感： 对于噪声和缺失数据具有较好的鲁棒性。

不足

• 对输入特征的独立性要求： 朴素贝叶斯分类器假设输入特征之间相互独立，这在某些实际问题中可能不成立。
• 无法学习特征之间的关系： 由于假设特征独立，不能很好地捕捉特征之间的复杂关系。
• 需要先验概率： 对先验概率的准确估计要求较多领域知识或足够的样本数据。

🍋实战代码

# 导入所需的库和模块
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics# 下载并加载20类新闻数据集
newsgroups = fetch_20newsgroups(subset='all', remove=('headers', 'footers', 'quotes'))# 特征工程: 将文本转换为TF-IDF表示
vectorizer = TfidfVectorizer(stop_words='english', max_features=1000)
X = vectorizer.fit_transform(newsgroups.data)# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, newsgroups.target, test_size=0.2, random_state=42)# 构建朴素贝叶斯分类器
classifier = MultinomialNB()
classifier.fit(X_train, y_train)# 在测试集上进行预测
y_pred = classifier.predict(X_test)# 输出分类报告
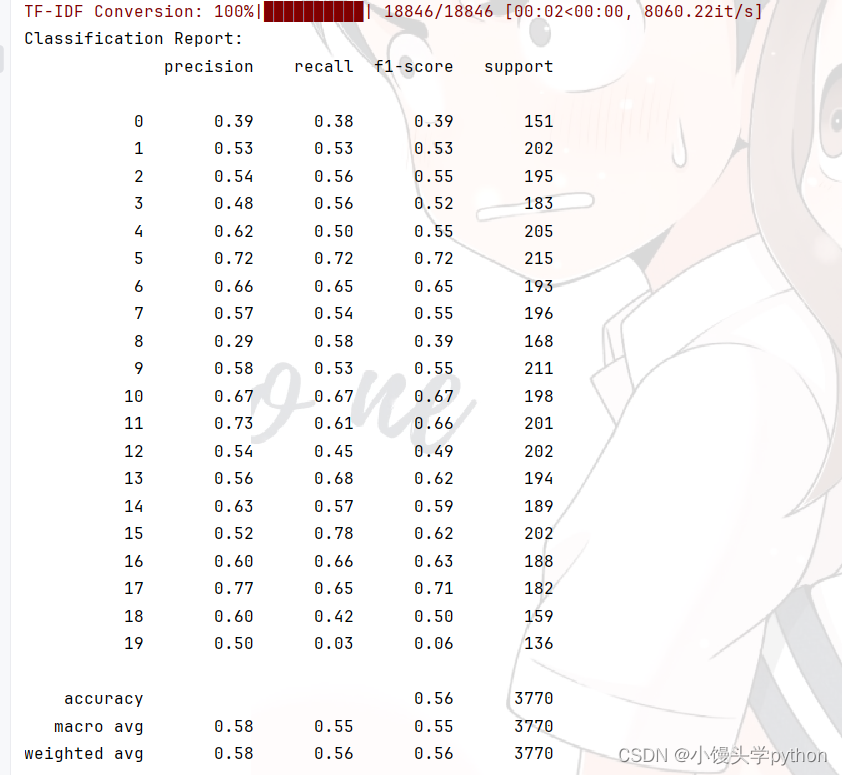
print("Classification Report:")
print(metrics.classification_report(y_test, y_pred))# 输出混淆矩阵
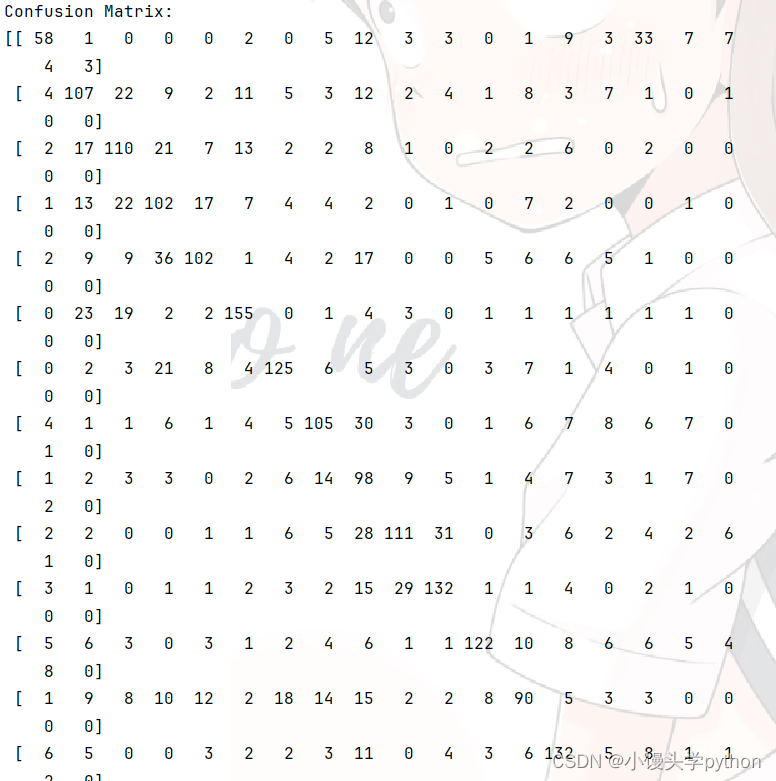
print("Confusion Matrix:")
print(metrics.confusion_matrix(y_test, y_pred))

运行结果如下

🍋结语

贝叶斯分类作为一种基于统计学习的方法，在实际问题中展现了良好的性能。通过充分利用先验知识和观测数据，贝叶斯分类为我们提供了一种有效的分类工具，特别在小样本场景和文本分类等任务中表现出色。

挑战与创造都是很痛苦的，但是很充实。