COMSOL Multiphysics® 软件中的模型都是从零开始构建的,软件支持多物理场,因此用户可以按照自己的意愿轻松地组合代表不同物理场现象的模型。有时这可以通过使用软件的内置功能来实现,但有些情况下,用户需要做一些额外的工作。我们以构建磁流体动力学(MHD)模型为例介绍一下这个工作流程。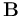 ,使得具有导电性
,使得具有导电性 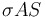 以一定速度
以一定速度 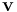 移动通过该磁场,从而产生感应电流。
移动通过该磁场,从而产生感应电流。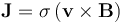 。除了这些感应电流之外,由于电势场的边界条件,还会产生电流
。除了这些感应电流之外,由于电势场的边界条件,还会产生电流 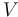 ,因此流体中的总电流变为:
,因此流体中的总电流变为: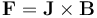 ,并将流体从一个容器泵送到另一个容器。我们假设系统在稳定状态下运行。
,并将流体从一个容器泵送到另一个容器。我们假设系统在稳定状态下运行。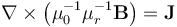 和
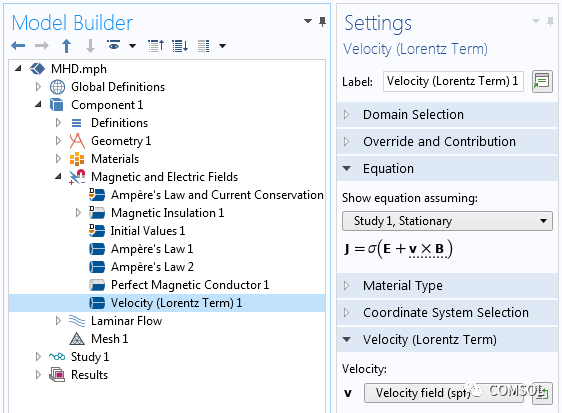
和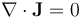 这组方程通过磁场和电场接口(AC/DC模块的一部),使用安培定律和电流守恒特征以及单独的速度(洛伦兹项) 特征求解。在移动流体周围的空间中,没有电流,所以我们只需求解单矢量方程:
这组方程通过磁场和电场接口(AC/DC模块的一部),使用安培定律和电流守恒特征以及单独的速度(洛伦兹项) 特征求解。在移动流体周围的空间中,没有电流,所以我们只需求解单矢量方程: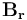 是剩余磁通密度,它仅在磁域中非零。当单独求解上述方程时,请使用磁场和电场接口中的安培定律特征。我们假设通道壁的属性不影响场,因此在模型中忽略它们。使用一组材料属性和边界条件来给出说明性结果。任何位置的磁场边界条件都是磁绝缘条件, xy 平面除外,该平面采用理想磁导体条件来利用系统的对称性。表示电极的域必须一直延伸到建模域的边界,接触磁绝缘边界,以提供电流返回路径。电压型接地和终端条件应用于这些外表面,而电绝缘条件应用于所有其他适用的边界。此外,我们还需要求解通道中的流场。我们假设流动是层流,从而在通道域中求解纳维-斯托克斯方程。如果流动是湍流,我们可以添加一个湍流模型。开放边界条件应用于通道的两端,表压为零。对称条件应用于 xy 平面。计算域如下图所示。
是剩余磁通密度,它仅在磁域中非零。当单独求解上述方程时,请使用磁场和电场接口中的安培定律特征。我们假设通道壁的属性不影响场,因此在模型中忽略它们。使用一组材料属性和边界条件来给出说明性结果。任何位置的磁场边界条件都是磁绝缘条件, xy 平面除外,该平面采用理想磁导体条件来利用系统的对称性。表示电极的域必须一直延伸到建模域的边界,接触磁绝缘边界,以提供电流返回路径。电压型接地和终端条件应用于这些外表面,而电绝缘条件应用于所有其他适用的边界。此外,我们还需要求解通道中的流场。我们假设流动是层流,从而在通道域中求解纳维-斯托克斯方程。如果流动是湍流,我们可以添加一个湍流模型。开放边界条件应用于通道的两端,表压为零。对称条件应用于 xy 平面。计算域如下图所示。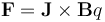 。这个力的表达式没有内置到软件中,所以在这里我们需要做一些手工操作。我们需要找到电流和磁场分量的内置表达式,可以通过查看方程视图并生成报告来实现,如知识库条目中关于实现用户定义的多物理场耦合的描述。这些内置表达式用于定义流体上的体积力,如下面的屏幕截图所示。
。这个力的表达式没有内置到软件中,所以在这里我们需要做一些手工操作。我们需要找到电流和磁场分量的内置表达式,可以通过查看方程视图并生成报告来实现,如知识库条目中关于实现用户定义的多物理场耦合的描述。这些内置表达式用于定义流体上的体积力,如下面的屏幕截图所示。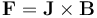 由于电流和磁场而对流体施加一个力,还有一个方程
由于电流和磁场而对流体施加一个力,还有一个方程  ),那么我们将当前的方程简化为:
),那么我们将当前的方程简化为: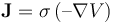 。这意味着流体流动问题不会影响电流,流动方程可以与电磁场方程完全分开求解。也就是说,我们可以首先求解电磁场,一旦知道了电磁场,就使用这些场作为流动问题的输入,从而使问题单向耦合。我们还可以进行额外的简化。严格地说,磁场是由磁铁和电流引起的。然而,对于我们这里分析的边界条件和材料特性,由于电流产生的磁场远小于由磁体引起的磁场。因此,我们可以做出简化的假设,即磁场仅仅是由于磁铁而产生的;也就是说,电流不会产生明显的磁场。这样,我们可以在无电流假设下求解磁场,并分别使用磁场,无电流和电流接口求解电流。这些物理场接口具有与前面讨论的类似的一组边界和域条件。磁场,无电流接口定义了方程
。这意味着流体流动问题不会影响电流,流动方程可以与电磁场方程完全分开求解。也就是说,我们可以首先求解电磁场,一旦知道了电磁场,就使用这些场作为流动问题的输入,从而使问题单向耦合。我们还可以进行额外的简化。严格地说,磁场是由磁铁和电流引起的。然而,对于我们这里分析的边界条件和材料特性,由于电流产生的磁场远小于由磁体引起的磁场。因此,我们可以做出简化的假设,即磁场仅仅是由于磁铁而产生的;也就是说,电流不会产生明显的磁场。这样,我们可以在无电流假设下求解磁场,并分别使用磁场,无电流和电流接口求解电流。这些物理场接口具有与前面讨论的类似的一组边界和域条件。磁场,无电流接口定义了方程 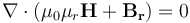 ,该方程的计算量远低于磁场和电场接口中定义的方程组。此外,这个方程可以独立于电流求解。
,该方程的计算量远低于磁场和电场接口中定义的方程组。此外,这个方程可以独立于电流求解。
磁流体动力学的多物理场建模
MHD 现象的建模本质上是一个多物理场问题;必须用数值方法求解流体流动、电流和磁场之间的耦合问题。这些不同的场都是由偏微分方程描述的,可以通过有限元方法求解。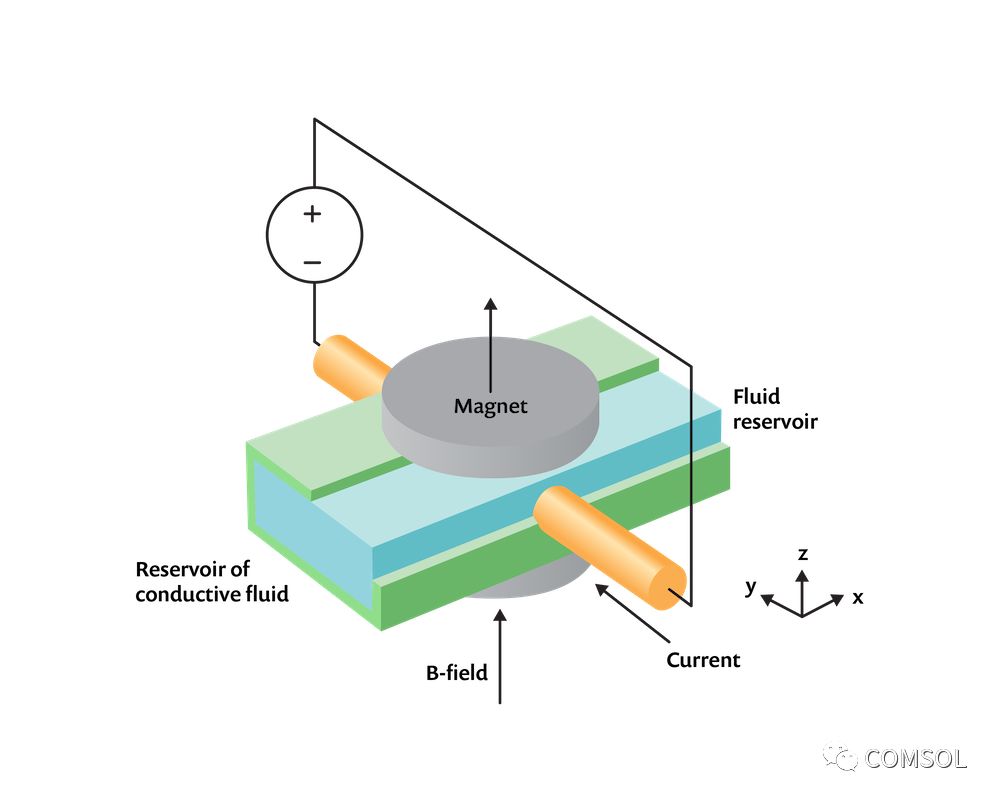
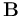 ,使得具有导电性
,使得具有导电性 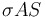 以一定速度
以一定速度 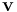 移动通过该磁场,从而产生感应电流。
移动通过该磁场,从而产生感应电流。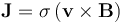 。除了这些感应电流之外,由于电势场的边界条件,还会产生电流
。除了这些感应电流之外,由于电势场的边界条件,还会产生电流 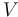 ,因此流体中的总电流变为:
,因此流体中的总电流变为: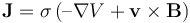
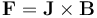 ,并将流体从一个容器泵送到另一个容器。我们假设系统在稳定状态下运行。
,并将流体从一个容器泵送到另一个容器。我们假设系统在稳定状态下运行。耦合电场、磁场和流场
对于这个问题,我们需要求解流体中的偏微分方程组来描述电场和磁场。方程式为: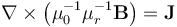 和
和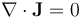 这组方程通过磁场和电场接口(AC/DC模块的一部),使用安培定律和电流守恒特征以及单独的速度(洛伦兹项) 特征求解。在移动流体周围的空间中,没有电流,所以我们只需求解单矢量方程:
这组方程通过磁场和电场接口(AC/DC模块的一部),使用安培定律和电流守恒特征以及单独的速度(洛伦兹项) 特征求解。在移动流体周围的空间中,没有电流,所以我们只需求解单矢量方程: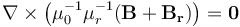
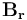 是剩余磁通密度,它仅在磁域中非零。当单独求解上述方程时,请使用磁场和电场接口中的安培定律特征。我们假设通道壁的属性不影响场,因此在模型中忽略它们。使用一组材料属性和边界条件来给出说明性结果。任何位置的磁场边界条件都是磁绝缘条件, xy 平面除外,该平面采用理想磁导体条件来利用系统的对称性。表示电极的域必须一直延伸到建模域的边界,接触磁绝缘边界,以提供电流返回路径。电压型接地和终端条件应用于这些外表面,而电绝缘条件应用于所有其他适用的边界。此外,我们还需要求解通道中的流场。我们假设流动是层流,从而在通道域中求解纳维-斯托克斯方程。如果流动是湍流,我们可以添加一个湍流模型。开放边界条件应用于通道的两端,表压为零。对称条件应用于 xy 平面。计算域如下图所示。
是剩余磁通密度,它仅在磁域中非零。当单独求解上述方程时,请使用磁场和电场接口中的安培定律特征。我们假设通道壁的属性不影响场,因此在模型中忽略它们。使用一组材料属性和边界条件来给出说明性结果。任何位置的磁场边界条件都是磁绝缘条件, xy 平面除外,该平面采用理想磁导体条件来利用系统的对称性。表示电极的域必须一直延伸到建模域的边界,接触磁绝缘边界,以提供电流返回路径。电压型接地和终端条件应用于这些外表面,而电绝缘条件应用于所有其他适用的边界。此外,我们还需要求解通道中的流场。我们假设流动是层流,从而在通道域中求解纳维-斯托克斯方程。如果流动是湍流,我们可以添加一个湍流模型。开放边界条件应用于通道的两端,表压为零。对称条件应用于 xy 平面。计算域如下图所示。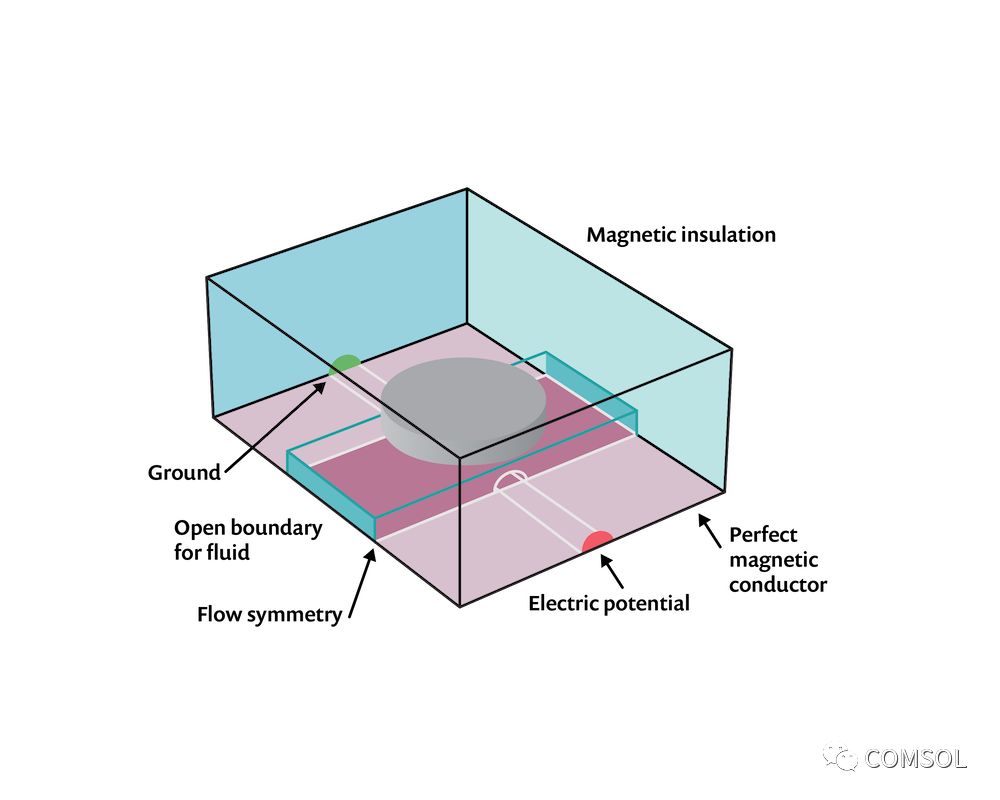
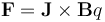 。这个力的表达式没有内置到软件中,所以在这里我们需要做一些手工操作。我们需要找到电流和磁场分量的内置表达式,可以通过查看方程视图并生成报告来实现,如知识库条目中关于实现用户定义的多物理场耦合的描述。这些内置表达式用于定义流体上的体积力,如下面的屏幕截图所示。
。这个力的表达式没有内置到软件中,所以在这里我们需要做一些手工操作。我们需要找到电流和磁场分量的内置表达式,可以通过查看方程视图并生成报告来实现,如知识库条目中关于实现用户定义的多物理场耦合的描述。这些内置表达式用于定义流体上的体积力,如下面的屏幕截图所示。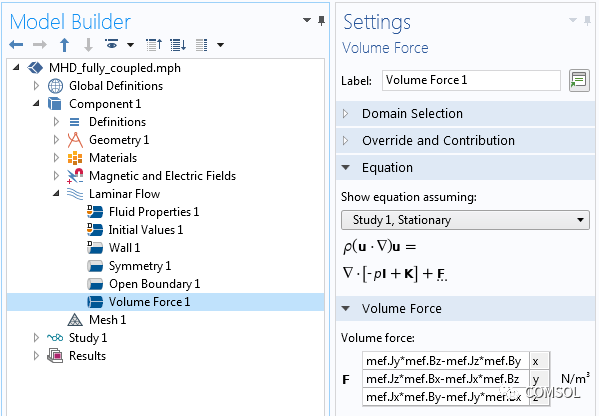
MHD 问题的网格划分和求解
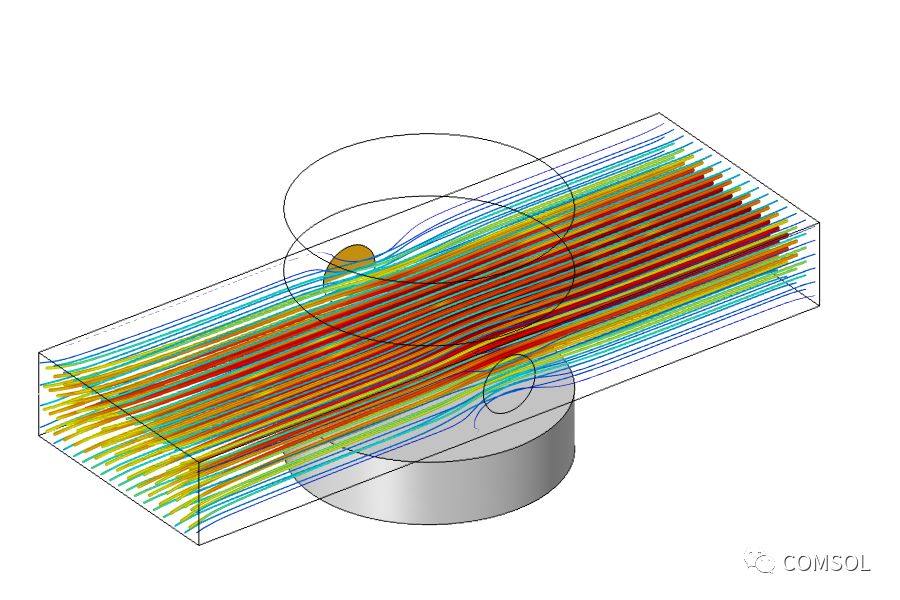
说到单元网格划分和单元阶次,这里一个重要的问题是模型的计算量。求解流体和周围域中的磁场和电场是模型中计算量最大的部分,因此我们希望将整个模型中的网格单元总数保持最少。基于线性静态问题的一些经验法则,我们可以说至少具有二阶单元是一个很好的起点。因此,我们将流体流动的离散化转换为 P2 + P2 离散化,这意味着速度和压力都用二阶基函数来描述。磁场和电场都用二阶离散化来描述。由于所有场都被离散化为至少二阶,因此几何形状的阶次也将自动变为二阶。对可选网格阶次和网格大小的全面调查留给有积极性的读者作为练习。求解时,软件将自动采用所谓的分离方法,在确定电磁场和速度场之间来回切换,并计算这些场的线性子系统,每个子系统都有自己的优化迭代求解器。由于这种多物理场问题本质上是非线性的,因此了解解决此类问题时可能出现的难题以及如何解决这些难题通常也很有帮助,正如此条知识库条目中关于提高非线性稳态模型的收敛性所述。多物理场分析的结果如下图所示。我们观察到明显的泵送效应:施加的电压导致电流流过流体,当这些电荷在磁场中移动时,它们会受到一个力的作用,这个力被传递给流体。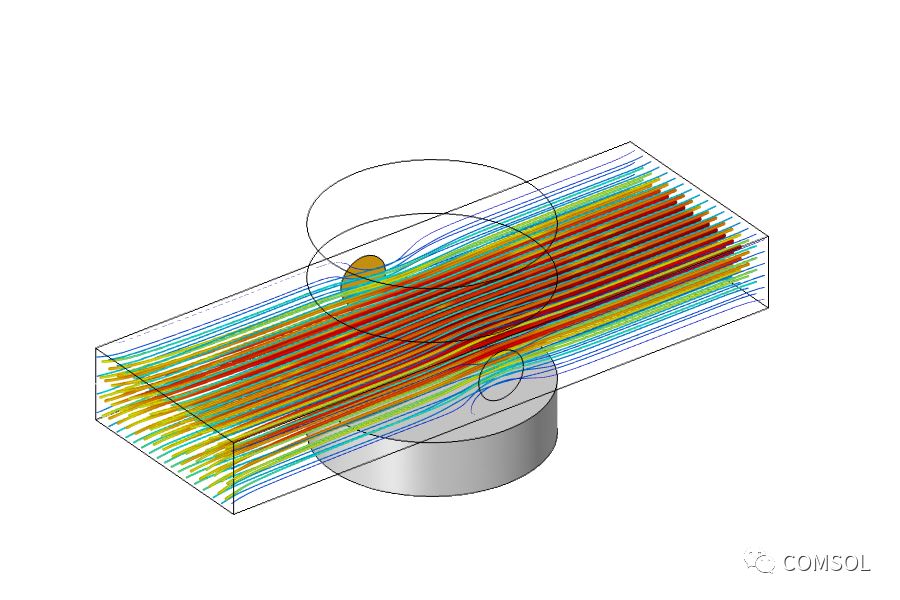
由于 MHD 多物理场耦合引起的流体泵送的结果图。
简化 MHD 模型
到目前为止,我们已经建立了一个包括磁场、电流和流体流动的模型,我们考虑了所有物理场方程之间的双向耦合。也就是说,每一种物理场现象都会影响其他物理场现象。但事实证明,对于这种特殊情况,我们不需要这样做。接下来我们看一下其中的原因,以及它如何让我们的模型更简单。如果我们回过头来看一下之前的所有控制方程,我们可以看到只有两个方程引入了物理场现象之间的耦合。方程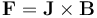 由于电流和磁场而对流体施加一个力,还有一个方程
由于电流和磁场而对流体施加一个力,还有一个方程 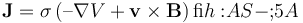
 ),那么我们将当前的方程简化为:
),那么我们将当前的方程简化为: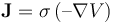 。这意味着流体流动问题不会影响电流,流动方程可以与电磁场方程完全分开求解。也就是说,我们可以首先求解电磁场,一旦知道了电磁场,就使用这些场作为流动问题的输入,从而使问题单向耦合。我们还可以进行额外的简化。严格地说,磁场是由磁铁和电流引起的。然而,对于我们这里分析的边界条件和材料特性,由于电流产生的磁场远小于由磁体引起的磁场。因此,我们可以做出简化的假设,即磁场仅仅是由于磁铁而产生的;也就是说,电流不会产生明显的磁场。这样,我们可以在无电流假设下求解磁场,并分别使用磁场,无电流和电流接口求解电流。这些物理场接口具有与前面讨论的类似的一组边界和域条件。磁场,无电流接口定义了方程
。这意味着流体流动问题不会影响电流,流动方程可以与电磁场方程完全分开求解。也就是说,我们可以首先求解电磁场,一旦知道了电磁场,就使用这些场作为流动问题的输入,从而使问题单向耦合。我们还可以进行额外的简化。严格地说,磁场是由磁铁和电流引起的。然而,对于我们这里分析的边界条件和材料特性,由于电流产生的磁场远小于由磁体引起的磁场。因此,我们可以做出简化的假设,即磁场仅仅是由于磁铁而产生的;也就是说,电流不会产生明显的磁场。这样,我们可以在无电流假设下求解磁场,并分别使用磁场,无电流和电流接口求解电流。这些物理场接口具有与前面讨论的类似的一组边界和域条件。磁场,无电流接口定义了方程 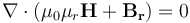 ,该方程的计算量远低于磁场和电场接口中定义的方程组。此外,这个方程可以独立于电流求解。
,该方程的计算量远低于磁场和电场接口中定义的方程组。此外,这个方程可以独立于电流求解。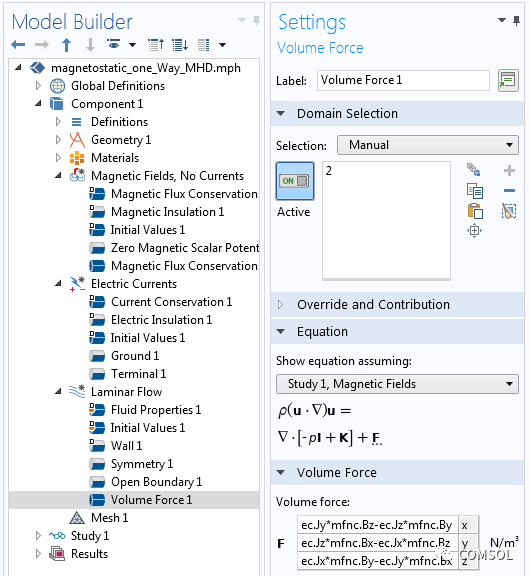

推荐阅读
分析大型强子对撞机的超导磁体失超如何在 COMSOL 软件中对铁磁材料进行建模?



















