大多数学校的统计学悲剧在于它是多么愚蠢。老师们花费数小时来研究导数，方程式和定理，当您最终达到最佳效果时（将概念应用于实际数字），就会出现一些无关紧要，没有想象力的示例，例如掷骰子。遗憾的是，如果您跳过推导（您可能永远不需要），而专注于使用这些想法来解决有趣的问题，那么统计数据就很有趣。

如果随机变量是什么我们都不清楚，那我们还在讨论什么！

随机变量在统计和概率中非常重要的概念，必须先具有随机变量，才会有后续概率分布的概念。 另外，初学者会经常把随机变量与传统变量混淆。基于以上原因，在此文章中，我们将阐述两点：

1. 什么是随机变量？
2. 为什么我们需要它们而不是传统变量。

在概率统计中，随机变量(随机数量)： 变量中的值是随机现象的结果（a variable whose possible values are the outcomes of a random phenomenon）。

就其取值而言，随机变量与我们的传统变量不同。它是随机结果映射的数值，另外由于它受随机性的影响，因此随机变量取不同的值。

1. 为什么称为随机变量？

随机变量使我们能够以数学方式进行提问。例如：

如果我们掷5个硬币，请回答以下问题：

1. 获得3个正面的概率是多少？
2. 获得少于4个正面的概率是多少？
3. 获得超过1个正面的概率是多少？

第一步，用函数p（）来描述概率的概念

那么我们的一般方式将是： P（抛硬币5次时恰好获得3个正面的概率） P（抛硬币5次时少于4个正面的概率） P（抛硬币5次时获得超过1个正面的概率）

第二步，用随机变量的方式表达括号内的自然语言

我们使用随机变量来表示上述问题，那么我们将编写：

1. P（X = 3）
2. P（X <4）
3. P（X > 1）

其中X 表示 抛硬币获得正面的次数。

正如我们在上面看到的，随机变量使我们更容易量化任何随机过程的结果，并将结果应用于数学并执行进一步的数值计算，毕竟如果不量化，“硬币正面” 这样的描述是无法进行科学计算的。

更一般的：

假设我们有一个抛硬币的随机过程/实验。两种可能结果之一可能是正面，也可能是反面。因此，这里我们使用X来表示随机变量，它表示此随机过程的结果。

因此我们可以写：

X = 1，如果结果是正面 X = 0，如果结果是反面

在这里，随机变量X将随机过程（掷硬币）的结果（正、反）映射到数值（1、0）。

分配给表示正面和反面的值可以是任何数字，不一定是1和0。

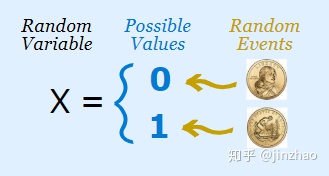
只是为了使理解更简单或更容易后续计算，我们使用了1和0。

将数字值分配给随机过程的结果的其他方法可能是： X = 100（如果结果为正面） X = 50，如果结果是反面

总结三点：

1. 我们有一个实验（扔硬币）
2. 我们为每个事件赋予价值
3. 这些值集是一个随机变量。

2. 随机变量与代数中使用的传统变量有何不同？

假设代数中使用的变量为x，y，z。在这里，x可以是手机的数量，y = 正面的数量 或z =学生数。变量只是代表未知数字的字母字符。

例如： x + 5 = 10 x是其值未知的变量，我们正在尝试查找其值。 评估后，x = 5。

随机变量不同于代数中的变量，因为它具有一组完整的值，并且可以随机获取任何值。代数中使用的变量一次不能具有多个值。

如果随机变量X = {0,1,2,3} 那么X可以是随机的0、1、2或3，其中每个都有不同的概率。

我们将大写字母用于随机变量，以避免与传统变量混淆。

随机变量可以是离散的也可以是连续的。

如果变量可以采用可计数数量的不同值，则它是离散的随机变量。

例如：

1. 在扔2个硬币的实验中，我们需要找出可能的正面数。 在这种情况下，X是随机变量，它可能取的值是离散的0、1和2。 因此X = {0，1，2}
2. 如果随机变量在一个间隔中取无限数量的值，则称该变量为连续变量。 例如：假设一个城市的温度在摄氏30度到45度之间。温度可以在30⁰至45⁰之间取任意值。因此温度可以是30.13⁰或40.15⁰，也可以是30.13⁰和40.15⁰。当我们说温度为38⁰时，表示温度在37.5至38.5之间。因此，在连续随机变量中没有精确或离散的观测值。

这是随机变量的简要介绍。

谢谢阅读！！