本文主要简单阐述爬山法的基本算法思想,并给出用此算法实现八皇后问题详细过程
最基本的爬上搜索算法表示:(节选自《人工智能》第二版):
function HILL-CLIMBING(problem) return a state thate is a locak maximum
inputs: problem
local variables: current, a node
neighbor,a node
current = MakeNode(INITAL-STATE(problem));
loop do
neighbor = a highest-valued successor of current ;
if VALUE[neighbor] <= VALUE[current] then return STATE[current];
current = neighbor ;
算法特点:
爬山法是一个向值增加的方向持续移动的简单循环过程--类似于登高,它将会在到达一个“峰顶”时终止,此时相邻状态中没有比它更高的值。这个算法不会维护搜索树,因此当前节点的数据结构只需要记录当前状态和它的目标函数值,它不会前瞻与当前状态不直接相邻的那些状态的值。这里更高的值是根据具体的应用场景来定的,准确的说是更接近目标状态的值,由我们设置的启发式函数来决定哪个值更好,比如我们求解八皇后问题更高的值就是当前格局中皇后冲突对数最少的情况
算法局限性:
爬山法属于一种局部的贪婪搜索方法,当它在搜索过程中遇到了局部最大值就很难继续向下搜索了,局部极大值是一个比它的每个邻居状态都高得到峰顶,但是比全局最大值(我们要到达的最终状态)要低,爬山法算法到达局部极大值附近就会被拉向峰顶,然后卡在局部极大值处无处可走。因此产生了爬山法的变种如随机爬山法及其变种如随机爬山法,随机重新开始的爬山法,模拟退火搜索能够非常有效的解决N皇后问题。
求解八皇后问题:
- #-*- coding: utf-8 -*-
-
- import random
- #函数一:参数为当前棋盘布局状态,根据布局判断当前八皇后布局存在冲突的皇后对数
- def get_numof_conflict(status):
- num = 0
- for i in range(len(status)):
- for j in range(i + 1,len(status)):
-
- if status[i] == status[j]:
- num += 1
- offset = j - i
- if abs(status[i]-status[j]) == offset:
- num += 1
- return num
- #函数二:参数为当前棋盘布局状态,利用爬山法思想选择邻居状态最好的布局并返回
- def hill_climbing(status):
- convert = {}
- length = len(status)
- for col in range(length):
- best_move = status[col]
- for row in range(length):
- if status[col] == row:
- continue
- status_copy = list(status)
- status_copy[col] = row
- convert[(col,row)] = get_numof_conflict(status_copy)
-
- answers = [] #最佳后继集合
- conflict_now = get_numof_conflict(status) #当前皇后冲突对数
-
- #遍历存储所有可能后继的字典,找出最佳后继
- for key,value in convert.iteritems():
- if value < conflict_now:
- conflict_now = value
- for key,value in convert.iteritems():
- if value == conflict_now:
- answers.append(key)
-
- #如果最佳后继集合元素大于一个 随机选择一个
- if len(answers) > 0:
- x = random.randint(0,len(answers)-1)
- col = answers[x][0]
- row = answers[x][1]
- status[col] = row
-
- return status
-
- #函数三:求得八皇后满足冲突数为0的一个解,循环输出每一步的后继集合 直到不存在冲>突为止
- def Queens():
- status = [0,1,2,3,4,5,6,7] #初始状态所有皇后都在对角线
-
- #当存在冲突的个数大于0时 循环求解最佳后继 直到找到八皇后解
- while get_numof_conflict(status) > 0:
- status = hill_climbing(status)
- print status
- print get_numof_conflict(status)
- print "the answer is"
- print
- print status
-
- if __name__ == '__main__':
- Queens()
-
(1)启发式耗散函数 get_numof_conflict求出可以彼此攻击2的皇后对的数 hill_climbing是算法中爬山过程的实现,convert字典中存储的键是所有可能后继状态,值是此状态对应的皇后冲突对数,后面通过遍历来找到最佳后继。爬山法算法通常在最佳后继集合中随机选择一个进行扩展,如果这样的后继多于一个的话
(2) 棋盘的排列用列表 status 表示, 依次表示第一列第二列到第n列的摆放位置。 如列表[0,2,1] 表示3*3矩阵第一列皇后放在最下面一格,第二列放在最上面一格,第三列放在中间一格
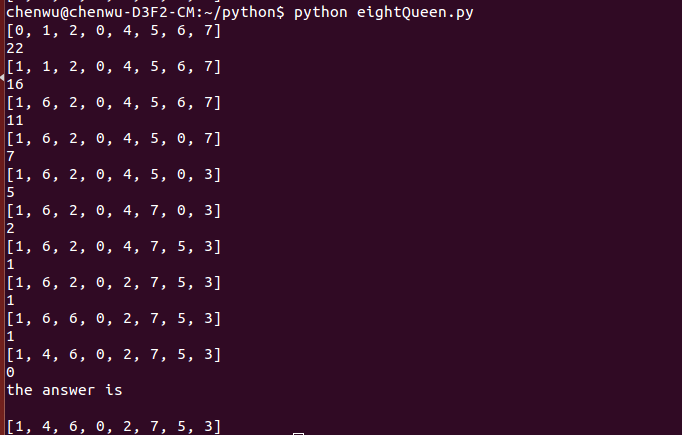
(3) 运行结果说明:初始状态每个皇后都在次对角线上 每次运行程序将输出求解一个八皇后正确解的爬山法实现过程 ,依次输出求解过程每一个最佳选择的邻居状态和其存在的皇后冲突对数,可以看出在求解过程中 不断爬山的过程--每进行一步都达到一个更好的格局,冲突次数更少,最后一行显示的是八皇后的一个正确解 冲突数为 0
运行截图
本文主要简单阐述爬山法的基本算法思想,并给出用此算法实现八皇后问题详细过程
最基本的爬上搜索算法表示:(节选自《人工智能》第二版):
function HILL-CLIMBING(problem) return a state thate is a locak maximum
inputs: problem
local variables: current, a node
neighbor,a node
current = MakeNode(INITAL-STATE(problem));
loop do
neighbor = a highest-valued successor of current ;
if VALUE[neighbor] <= VALUE[current] then return STATE[current];
current = neighbor ;
算法特点:
爬山法是一个向值增加的方向持续移动的简单循环过程--类似于登高,它将会在到达一个“峰顶”时终止,此时相邻状态中没有比它更高的值。这个算法不会维护搜索树,因此当前节点的数据结构只需要记录当前状态和它的目标函数值,它不会前瞻与当前状态不直接相邻的那些状态的值。这里更高的值是根据具体的应用场景来定的,准确的说是更接近目标状态的值,由我们设置的启发式函数来决定哪个值更好,比如我们求解八皇后问题更高的值就是当前格局中皇后冲突对数最少的情况
算法局限性:
爬山法属于一种局部的贪婪搜索方法,当它在搜索过程中遇到了局部最大值就很难继续向下搜索了,局部极大值是一个比它的每个邻居状态都高得到峰顶,但是比全局最大值(我们要到达的最终状态)要低,爬山法算法到达局部极大值附近就会被拉向峰顶,然后卡在局部极大值处无处可走。因此产生了爬山法的变种如随机爬山法及其变种如随机爬山法,随机重新开始的爬山法,模拟退火搜索能够非常有效的解决N皇后问题。
求解八皇后问题:
- #-*- coding: utf-8 -*-
-
- import random
- #函数一:参数为当前棋盘布局状态,根据布局判断当前八皇后布局存在冲突的皇后对数
- def get_numof_conflict(status):
- num = 0
- for i in range(len(status)):
- for j in range(i + 1,len(status)):
-
- if status[i] == status[j]:
- num += 1
- offset = j - i
- if abs(status[i]-status[j]) == offset:
- num += 1
- return num
- #函数二:参数为当前棋盘布局状态,利用爬山法思想选择邻居状态最好的布局并返回
- def hill_climbing(status):
- convert = {}
- length = len(status)
- for col in range(length):
- best_move = status[col]
- for row in range(length):
- if status[col] == row:
- continue
- status_copy = list(status)
- status_copy[col] = row
- convert[(col,row)] = get_numof_conflict(status_copy)
-
- answers = [] #最佳后继集合
- conflict_now = get_numof_conflict(status) #当前皇后冲突对数
-
- #遍历存储所有可能后继的字典,找出最佳后继
- for key,value in convert.iteritems():
- if value < conflict_now:
- conflict_now = value
- for key,value in convert.iteritems():
- if value == conflict_now:
- answers.append(key)
-
- #如果最佳后继集合元素大于一个 随机选择一个
- if len(answers) > 0:
- x = random.randint(0,len(answers)-1)
- col = answers[x][0]
- row = answers[x][1]
- status[col] = row
-
- return status
-
- #函数三:求得八皇后满足冲突数为0的一个解,循环输出每一步的后继集合 直到不存在冲>突为止
- def Queens():
- status = [0,1,2,3,4,5,6,7] #初始状态所有皇后都在对角线
-
- #当存在冲突的个数大于0时 循环求解最佳后继 直到找到八皇后解
- while get_numof_conflict(status) > 0:
- status = hill_climbing(status)
- print status
- print get_numof_conflict(status)
- print "the answer is"
- print
- print status
-
- if __name__ == '__main__':
- Queens()
-
(1)启发式耗散函数 get_numof_conflict求出可以彼此攻击2的皇后对的数 hill_climbing是算法中爬山过程的实现,convert字典中存储的键是所有可能后继状态,值是此状态对应的皇后冲突对数,后面通过遍历来找到最佳后继。爬山法算法通常在最佳后继集合中随机选择一个进行扩展,如果这样的后继多于一个的话
(2) 棋盘的排列用列表 status 表示, 依次表示第一列第二列到第n列的摆放位置。 如列表[0,2,1] 表示3*3矩阵第一列皇后放在最下面一格,第二列放在最上面一格,第三列放在中间一格
(3) 运行结果说明:初始状态每个皇后都在次对角线上 每次运行程序将输出求解一个八皇后正确解的爬山法实现过程 ,依次输出求解过程每一个最佳选择的邻居状态和其存在的皇后冲突对数,可以看出在求解过程中 不断爬山的过程--每进行一步都达到一个更好的格局,冲突次数更少,最后一行显示的是八皇后的一个正确解 冲突数为 0
运行截图







)











