BF算法是基于主串指针回溯,重新与子串进行逐字符进行比较,主串为S什么要进行回溯呢,原因在于模式P中存在相同的字符或者说由字符(串)存在重复(模式的部分匹配性质),设想如果模式P中字符各不相同,主串就S的指针就根本不需要回溯;然而,我们可以发现在主串S与模式发生失配时,主串指针进行回溯会影响效率,因为由于模式S本身字符的部分部分匹配性质,回溯之后,主串S与模式T有些部分比较是没有必要的,这就是对BF算法所要改进的地方。
BF算法的执行过程:
例:S =″aaaaaaaaaaab″
T =″aaab″
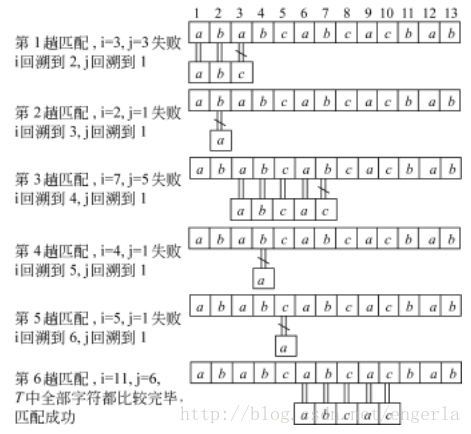
KMP算法的执行过程:
例:S =″ababcabcacbab″
T =″abcac″
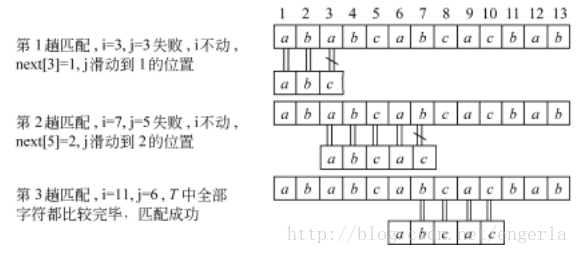
经过以上对比,我们可以发现KMP算法的效率要比BF算法的效率高,接下来看一下代码。
BF算法
BF算法思想
- 在串 S 和串 T 中分别设比较的起始下标 i 和 j;
- 循环直到 S 中所剩字符个数小于 T 的长度或 T 的所有字符均比较完
2 .1如果 S[i] = T [j] ,则继续比较 S 和 T 的下一个字符 ;
2 .2 如果S[i] != T [j],将 i 和 j 回溯 ,准备下一趟比较 ; - 如果 T 中所有字符均比较完 , 则匹配成功 , 返回匹配的起始比较下标 ;
否则 ,匹配失败 ,返回 0;
int BF(String S, String T, int pos) {//pos是进行模式匹配的起始位置int i = 0;int j = 0;int start = 0;//子串的起始位置if (pos < 0 || (pos + T.length >= S.length)) {//起始位置小于0或者起始位置加上模式串的长度大于主串的长度,就不用进行匹配了printf("Irregular position.\n");} else {//进行匹配i = pos - 1;while (i < S.length && j < T.length) {if (S.str[i] == T.str[j]) {if (j == 0) {start = i;//记录子串的起始位置}i++;j++;} else {//若前面的字符都不同,tag一直为0,所以必须分情况讨论if (j != 0) {i = start + 1;} else {i = i + 1;}j = 0;}}if (j == T.length) {printf("ok\n");printf("start position = %d\n", start + 1);} else {printf("bu ok\n");}}return (start + 1);//返回子串的起始位置的逻辑位置
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
KMP算法
KMP的算法中需要用到一个next数组,该数组是用来确定失配后模式串循环变量j回溯的位置的。
next数组的计算
在“aba”中,前缀是真前缀的所有子串的集合,包括“a”、“ab”,除去最后一个字符的剩余字符串叫做真前缀在“aba”中,真前缀“ab”。同理,真后缀就是除去第一个字符的后面全部的字符串。
next就是前缀和后缀中相同的子串的最大长度
例如:
1. 在“aba”中,前缀是“a”,后缀是“a”,那么两者相同子串最长的就是“a”,相同的子串的最的长度就是1;
2. 在“ababa”中,前缀是“aba”,后缀是“aba”,二者相同子串最长的是“aba”,相同的子串的最的长度就是3;
3. 在“abcabcdabc”中,前缀是“abc”,后缀是“abc”,二者相同子串最长的是“abc”,相同的子串的最的长度就是3;
这里有一点要注意,前缀必须要从头开始算,后缀要从最后一个数开始算,中间截一段相同字符串是不行的
next数组的计算还有简单的方法,上述使用最基础的方法计算的,便于理解
KMP算法思想
- 在串 S 和串 T 中分别设比较的起始下标 i 和 j;
- 循环直到 S 中所剩字符长度小于 T 的长度或 T 中所有字符均比较完毕
2 .1 如果 S[i] = T [j],则继续比较 S 和 T 的下一个字符 ;
2 .2 如果S[i] != T [j],将 j 向右滑动到 next[ j] 位置 ,即 j = next[j] ;
2 .3 如果 j = 0 ,则将 i 和 j 分别加 1 ,准备下一趟比较; - 如果 T 中所有字符均比较完毕 , 则返回匹配的起始下标 ,否则返回 0;
此处next数组使用一种简单的方法计算的,此处就不过多解释了,可以去网上学习一下,网上资源很多
//计算next的值
void getNext(String T, int next[]) {int i;//循环变量int k;next[0] = -1;for (i = 1; T.str[i] != '\0'; ++i) {k = next[i - 1];while (k != -1) {if (T.str[i - 1] == T.str[k]) {next[i] = k + 1;break;} else {k = next[k];}}if (k == -1) {next[i] = 0;}}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
KMP算法的匹配
int KMP(String S, String T, int next[]) {int start = 0;int i = 0;//主串的循环变量int j = 0;//模式串的循环变量while (i < S.length && j < T.length) {if (S.str[i] == T.str[j]) {//若主串和模式串的字符相同,都向后移一位i++;j++;} else {//若失配了,模式串的循环变量就要根据next数组回溯j = next[j];if (j == -1) {i++;j++;//j=-1时,j必须要加1,否则下标越界导致运行出错}}}if (j == T.length) {//判断匹配是否成功start = i - T.length + 1;return start;}return -1;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
此外还需要做一些准备工作
#include <stdio.h>#define MAX_SIZE 100typedef struct {//定义一个字符串的结构体char str[MAX_SIZE];int length;//字符串的长度
} String;//初始化
int initString(String *S) {S->length = 0;return 1;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
用main函数测试一下
int main() {String S;//主串String T;//模式串initString(&S);//初始化initString(&T);createStr(&S);//从输入字符串createStr(&T);printf("----------BF&KMP----------\n");BF(S, T, 0);printf("----------KMP----------\n");int next[T.length];getNext(T, next);for (int i = 0; i < T.length; ++i) {printf("next[%d] = %d\t", i, next[i]);}printf("\n");int start = KMP(S, T, next);printf("\nstart position = %d\n", start);return 0;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
例:
S = “ababcabccabcacbab”
T = “abcac”
运行结果:
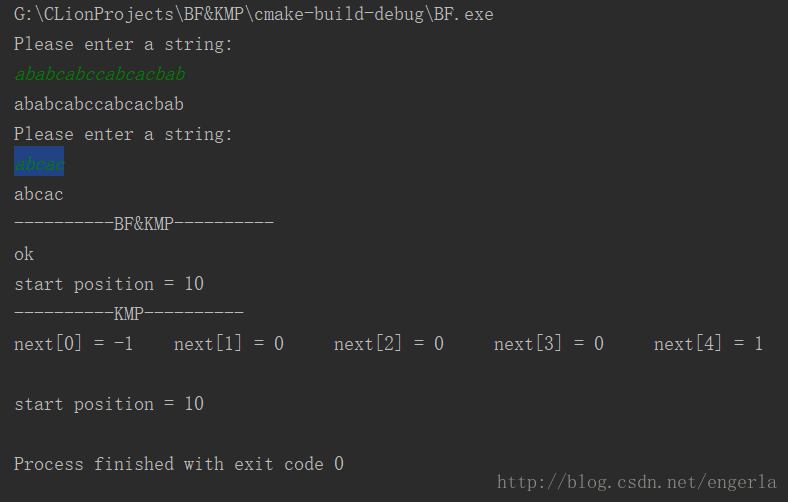









)



)





