本来很懵逼的 看到这篇文章基本全懂了
一般这种题目会让我感觉很是煎熬,不知道怎么算。终于打通这类题目,总结到这里。
先看这类题目的常见表述:如图所示,图中路由器采用存储–转发的方式,所有链路的传播速率均为100Mbps(可以是其他的数字),分组大小为1000B(同样可以是其他数字),其中分组头部大小(有些题可以忽略),分组拆装时间,传播延迟等可以忽略。本篇文章会说到不忽略也不影响宏观的数据传递时间,只在最后一个分组稍有影响。根据拓扑图,求传递大小为10MB的时间是多少。
首先,这里要说明M的区别,在10MB数据这里,是存储值,用的是1MB=220bits1MB=220bits.
这是很重要的区别。
我们知道从一个主机发送一段数据到另一个主机,需要经过计算机网络。这个过程有必要再阐述一次,以理清楚如何计算数据的传输时间消耗问题。
我们假设主机A到主机B.
一大块数据,先不管是一块直接传还是分成多组传输,而是先问,时间都去哪儿了?
主机A想,任务来了,得把它传到B,我才不管传的是B,C,D还是什么,我只知道要让它上路。
对的,上路,上的是什么路,上的是链路!
A其实像一个港口,目标是把货物装上集装箱,然后让集装箱坐船走。装箱的过程很耗时间,我们不能认为这个时间很短,就没了一个清晰的概念。
那么,这个送数据上路的时间怎么算?对的,就是传输速率,也称之为发送速率。
发送的过程很明确,根据链路的速率来发。
好的,现在数据发上链路了,其实就是电信号在链路上跑,以光速在跑。很多时候,在链路上的传播速度就不计了,好像瞬间就能到达与A相连的那个路由器。事实上可以这么认为。
我们就当经过一段很短的时间就从一个A传到了相连的路由器。
到这里,如果我问,A和B之间直接通过链路相连,A到B的时间算多少?
是不是瞬移?
不是的,装箱很耗时间啊!A要把数据送到链路上呢。
理解这个直连模型,就不用担心引入其他的路由器进来数据的传输问题了。因为,本质上,路由器也是电脑主机,和A传输东西没有区别,既然是存储–转发机制,就意味着数据进来路由器,再出去,还得经历一次装箱的流程。好像货物从A港口到了一个中转站,先把货物写下来,让轮船也休息休息,等休息好了(这个休息时间可类比为排队等,也可以认为休息时间不计),又得装箱。路由器也是这样,它也要重新装箱,上下一段链路,具体又得计算一次传输时间(发送时间)。
就这样每个路由器都这样算,到达B,终于不用计算B的存储转发时间了。
以上描述的过程,我们只看到一块的数据如何传输。
这里我先讲一个宏观的概念:整块传输的时间远大于分组传输的时间。
为什么会这样,直观来说就是,一大组每次都要存储–转发,计算的是n次。而分成多个组后,虽然过程相同,但是考虑到并行性,实际上我们只考虑一次大组数据的传输时间,那些细节的时间只用考虑最后一个分组即可!
实际上,上面这段话就讲完了所有的点。
而经过画图,计算,思考,只要分组连续发送的间隔相同,无论考不考虑排队时延,传播时延等,总的计算公式是:
分组时:
(总的数据量÷数据传输速率)+最后一个分组从第一段链路到终点的时间(总的数据量÷数据传输速率)+最后一个分组从第一段链路到终点的时间
有必要再多说最后一个分组传输的时间,我们考虑的是:A点将最后一个分组已经发送到了第一段链路,这个时刻正好是总的数据量除以链路传输速率的时间。
因此,我们只需要带着最后一段数据,计算从第一段链路到终点的时间即可。姑且认为,最后一个老幺被A关照了,送了它一程。
如果没有分组,也可以先拿总数据除以链路传输速率,再分析这个分组的传输。或者从A发送开始分析即可。
认识到这里,基本上此类题目无难题。
光说不练假把式。
实际动手来讨论一下。
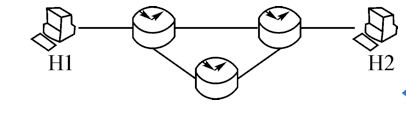
在下图所示的采用“存储-转发”方式的分组交换网络中,所有链路的数据传输速率为100 Mbps,分组大小为1000 B,其中分组头大小为20 B.若主机H1向主机H2发送一个大小为980 000 B的文考虑分组拆装时间和传播延迟的情况下,从H1发送开始到H2接收完为止,需要的时间至少是(C)
A. 80 ms B. 80.08 ms C. 80.16 ms D. 80.24 ms
解答:分组大小为1000B,设有xx个分组
那么:1000x=980,000+20x1000x=980,000+20x个分组。
就是简单的数学计算,不是凭直觉判断1000个分组的。
好了,1000个分组,按照我们形成的结论计算是:
总的数据量÷链路速率=(1000个分组⋅1000B)÷100Mbps=(106⋅8bit)÷(100⋅106bit/s)=80ms总的数据量÷链路速率=(1000个分组⋅1000B)÷100Mbps=(106⋅8bit)÷(100⋅106bit/s)=80ms
再考虑最后一个分组从第一段链路往H2用的时间:
很显然选择还剩两端链路,两个路由(就是从左到右的直线)的路径。
一个分组是1000B.
一个分组在一段链路上发送时间:
1000B÷100Mbps=(103⋅8bit)÷(100⋅106bit/s)=0.08ms1000B÷100Mbps=(103⋅8bit)÷(100⋅106bit/s)=0.08ms
发送两次用时就是0.16ms.
所以总时间是80.16ms.
有问题再继续补充。
update:或者用另一种角度想,总共n个分组,前面n-1个分组陆陆续续送上链路。当第n-1个分组送上链路后,用时为n−1个分组数据÷数据传输率n−1个分组数据÷数据传输率
此时看第n个分组就是从头开始,路径中多少链路就计算多少次。
比如上面的题目,就是999个分组数据÷数据传输率999个分组数据÷数据传输率,再加上第1000个分组从H1到H2经过三段链路的时间。
最初说总的数据量除以数据传输率+最后一个分组从第一段链路开始传输用时,不再计第一段传输用时,其实就是说第一段已经记在总的数据量里了。只是计算更方便些。原理相同。

)







 多项自定义)









